The evolution of anti-social rewarding and its countermeasures in public goods games - PubMed (original) (raw)
The evolution of anti-social rewarding and its countermeasures in public goods games
Miguel dos Santos. Proc Biol Sci. 2015.
Abstract
Cooperation in joint enterprises can easily break down when self-interests are in conflict with collective benefits, causing a tragedy of the commons. In such social dilemmas, the possibility for contributors to invest in a common pool-rewards fund, which will be shared exclusively among contributors, can be powerful for averting the tragedy, as long as the second-order dilemma (i.e. withdrawing contribution to reward funds) can be overcome (e.g. with second-order sanctions). However, the present paper reveals the vulnerability of such pool-rewarding mechanisms to the presence of reward funds raised by defectors and shared among them (i.e. anti-social rewarding), as it causes a cooperation breakdown, even when second-order sanctions are possible. I demonstrate that escaping this social trap requires the additional condition that coalitions of defectors fare poorly compared with pro-socials, with either (i) better rewarding abilities for the latter or (ii) reward funds that are contingent upon the public good produced beforehand, allowing groups of contributors to invest more in reward funds than groups of defectors. These results suggest that the establishment of cooperation through a collective positive incentive mechanism is highly vulnerable to anti-social rewarding and requires additional countermeasures to act in combination with second-order sanctions.
Keywords: cooperation; evolutionary games; pool rewards; social dilemmas.
© 2014 The Author(s) Published by the Royal Society. All rights reserved.
Figures
Figure 1.
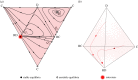
Anti-social rewarding in the PGG with reward funds and exclusion. The presence of anti-social rewarding results in a cooperation breakdown, even though second-order free-riders (i.e. non-rewarding individuals) can be excluded from their respective reward fund with an exclusion rate α that exceeds a critical threshold _α_T = (N – _r_2)/[_r_2(N – 1)]. Each face of the state space S4 is represented by a triangle. The interior of the triangles (a) and S4 (b) are filled with trajectories representing the dynamics of the population. The basic model without anti-social rewarding (corresponding to the triangle D–C–RC) could lead to full cooperation as the vertex RC was a global attractor. There is an unstable equilibrium _Q_2 between C and RC and between the three strategies D–C–RC _Q_1, but small perturbations such as random mutations will eventually lead the dynamics on this face towards the vertex RC. However, the presence of anti-social rewarding makes the vertex RC unstable and RD will be the outcome, starting from any initial condition. A similar unstable equilibrium _Q_3 is possible between D and RD, but perturbations will eventually lead the system towards RD. Interior states of S4 also end up in the vertex RD. Parameters: N = 5, _c_1 = 1, _r_1 = 3, _c_2 = 1, _r_2 = 3 and α = 0.2. (Online version in colour.)
Figure 2.
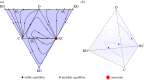
The interplay of exclusion and high rewarding efficacies for contributors in the PGG with reward funds. Full cooperation can be attained from any initial condition as rewarding players are able to sufficiently exclude second-order free-riders (i.e. non-rewarding individuals) from their corresponding reward fund (i.e. α > _α_T), and contributors are able to produce sufficient rewards to outcompete non-contributors (i.e. _c_3(_r_3 − 1) < _c_2(_r_2 − 1) − σ). (a) Unstable equilibria are possible between rewarding individuals and their corresponding non-rewarding type (i.e. _Q_1 between D and RD and _Q_2 between C and RC), but random perturbations will eventually lead the system to stable full cooperation. (b) Interior states of S4 also end up in the vertex RC. Parameters: N = 5, _c_1 = 1, _r_1 = 3, _c_2 = 1, _r_2 = 3, _c_3 = 1, _r_3 = 2 and α = 0.5. (Online version in colour.)
Figure 3.
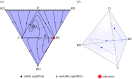
The interplay of exclusion and reward funds dependent on the public good produced. Full cooperation can be attained from any initial condition as rewarding players are able to sufficiently exclude second-order free-riders (i.e. non-rewarding individuals) from their corresponding reward fund (i.e. α > _α_T), and reward funds are raised with a fraction β of the public good produced. (a) An unstable equilibrium _Q_2 is possible between pro-social rewarders and their corresponding non-rewarding type. The whole edge D–RD is a line of fixed points because, in the absence of contributors, anti-social rewarders cannot invest in their reward fund. Random perturbations such as mutations will eventually lead the system to stable full cooperation. (b) Interior states of S4 also end up in the vertex RC. Parameters: N = 5, _c_1 = 1, _r_1 = 3, _r_2 = 3, β = 0.5 and α = 0.2. (Online version in colour.)
Similar articles
- Antisocial rewarding in structured populations.
Dos Santos M, Peña J. Dos Santos M, et al. Sci Rep. 2017 Jul 24;7(1):6212. doi: 10.1038/s41598-017-06063-9. Sci Rep. 2017. PMID: 28740243 Free PMC article. - Replicator dynamics in public goods games with reward funds.
Sasaki T, Unemi T. Sasaki T, et al. J Theor Biol. 2011 Oct 21;287:109-14. doi: 10.1016/j.jtbi.2011.07.026. Epub 2011 Aug 3. J Theor Biol. 2011. PMID: 21824483 - Antisocial pool rewarding does not deter public cooperation.
Szolnoki A, Perc M. Szolnoki A, et al. Proc Biol Sci. 2015 Oct 7;282(1816):20151975. doi: 10.1098/rspb.2015.1975. Proc Biol Sci. 2015. PMID: 26400746 Free PMC article. - On the interaction of the stick and the carrot in social dilemmas.
Milinski M, Rockenbach B. Milinski M, et al. J Theor Biol. 2012 Apr 21;299:139-43. doi: 10.1016/j.jtbi.2011.03.014. Epub 2011 Mar 31. J Theor Biol. 2012. PMID: 21458464 Review. - Review: Game theory of public goods in one-shot social dilemmas without assortment.
Archetti M, Scheuring I. Archetti M, et al. J Theor Biol. 2012 Apr 21;299:9-20. doi: 10.1016/j.jtbi.2011.06.018. Epub 2011 Jun 24. J Theor Biol. 2012. PMID: 21723299 Review.
Cited by
- Evolution of coordinated punishment to enforce cooperation from an unbiased strategy space.
García J, Traulsen A. García J, et al. J R Soc Interface. 2019 Jul 26;16(156):20190127. doi: 10.1098/rsif.2019.0127. Epub 2019 Jul 24. J R Soc Interface. 2019. PMID: 31337305 Free PMC article. - The study on the role of dedicators on promoting cooperation in public goods game.
Wu Z, Huang H, Liao Q. Wu Z, et al. PLoS One. 2021 Sep 20;16(9):e0257475. doi: 10.1371/journal.pone.0257475. eCollection 2021. PLoS One. 2021. PMID: 34543308 Free PMC article. - Reputation and punishment sustain cooperation in the optional public goods game.
Podder S, Righi S, Pancotto F. Podder S, et al. Philos Trans R Soc Lond B Biol Sci. 2021 Nov 22;376(1838):20200293. doi: 10.1098/rstb.2020.0293. Epub 2021 Oct 4. Philos Trans R Soc Lond B Biol Sci. 2021. PMID: 34601913 Free PMC article. - Benefits of asynchronous exclusion for the evolution of cooperation in stochastic evolutionary optional public goods games.
Quan J, Zheng J, Wang X, Yang X. Quan J, et al. Sci Rep. 2019 Jun 3;9(1):8208. doi: 10.1038/s41598-019-44725-y. Sci Rep. 2019. PMID: 31160674 Free PMC article. - Reputation effects drive the joint evolution of cooperation and social rewarding.
Pal S, Hilbe C. Pal S, et al. Nat Commun. 2022 Oct 7;13(1):5928. doi: 10.1038/s41467-022-33551-y. Nat Commun. 2022. PMID: 36207309 Free PMC article.
References
- West SA, El Mouden C, Gardner A. 2011. Sixteen common misconceptions about the evolution of cooperation in humans. Evol. Hum. Behav. 32, 231–262. (10.1016/j.evolhumbehav.2010.08.001) - DOI
- Oliver P. 1980. Rewards and punishments as selective incentives for collective action: theoretical investigations. Am. J. Sociol. 85, 1356–1375. (10.1086/227168) - DOI
- Ostrom E. 1990. Governing the commons: the evolution of institutions for collective action. New York, NY: Cambridge University Press.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources