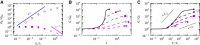Two fundamental mechanisms govern the stiffening of cross-linked networks - PubMed (original) (raw)
Two fundamental mechanisms govern the stiffening of cross-linked networks
Goran Žagar et al. Biophys J. 2015.
Abstract
Biopolymer networks, such as those constituting the cytoskeleton of a cell or biological tissue, exhibit a nonlinear strain-stiffening behavior when subjected to large deformations. Interestingly, rheological experiments on various in vitro biopolymer networks have shown similar strain-stiffening trends regardless of the differences in their microstructure or constituents, suggesting a universal stiffening mechanism. In this article, we use computer simulations of a random network comprised of cross-linked biopolymer-like fibers to substantiate the notion that this universality lies in the existence of two fundamental stiffening mechanisms. After showing that the large strain response is accompanied by the development of a stress path, i.e., a percolating path of axially stressed fibers and cross-links, we demonstrate that the strain stiffening can be caused by two distinctly different mechanisms: 1) the pulling out of stress-path undulations; and 2) reorientation of the stress path. The former mechanism is bending-dominated and can be recognized by a power-law dependence with exponent 3/2 of the shear modulus on stress, whereas the latter mechanism is stretching-dominated and characterized by a power-law exponent 1/2. We demonstrate how material properties of the constituents, as well as the network microstructure, can affect the transition between the two stiffening mechanisms and, as such, control the dominant power-law scaling behavior.
Copyright © 2015 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
Figure 1
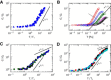
The nonlinear behavior of biopolymer networks plotted as the shear modulus, G, versus stress, T, or the shear modulus normalized by the initial shear modulus, G/_G_0, versus stress normalized by the critical stress at the onset of nonlinearity, T/Tc, for (A) F-actin/scruin networks (8); (B) F-actin/rigor-HMM networks with actin concentration 19 _μ_M, mean F-actin length 21 _μ_m, and various increasing molar HMM/actin concentration ratios, R=cHMM/ca (arrow) (13); (C) F-actin/filamin networks for lower F-actin concentrations (15); and (D) vimentin networks (39). To see this figure in color, go online.
Figure 2
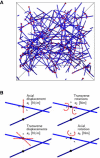
The cross-linked network model. (A) Example of a generated RVE with fibers shown in blue and cross-links in red. (B) A cross-link is a two-node element whose behavior is controlled by four independent spring constants. The cross-link is idealized by coupling the four spring constants to each other, s=s1=s3=s2/lc2=s4/lc2, where lc is the mean length of the fiber sections. The nondimensional system parameter s˜=slc3/κ used in our analysis, compares the cross-link stiffness to the fiber bending stiffness. To see this figure in color, go online.
Figure 3
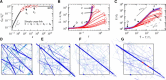
The effect of cross-link number s˜ of the networks with constant connectivity n˜X≈0.34, lc≈0.86μm. (A) The ensemble-averaged small strain response as a function of cross-link number s˜. The initial shear modulus, _G_0, is normalized by the initial network shear modulus in the rigidly cross-linked limit G0∞. The standard deviation is represented by the gray region. (B and C) The ensemble-averaged shear modulus, G˜=G/G0, as a function of strain, Γ, and normalized stress, T˜=T/Tc, respectively, for selected s˜ values, as indicated by the symbols in (A). The response of the RCL networks is shown in blue. Standard deviations (up to about twice the symbol size) are not shown. (D_–_G) View of the deformed network at stress states indicated by the letters in (B) and (C) for the RCL case at T˜≈1 (D), T˜≈20 (E), and T˜≈400 (F) and for s˜=104 at T˜≈500 (G). Filaments under tension/compression are shown in blue/light blue and cross-links in red. The thickness of a constituent is taken to be linearly proportional to its axial force normalized by the maximum axial force in the network, to help identify stress paths. To see this figure in color, go online.
Figure 4
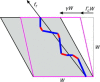
Simple shear of the box containing a percolating stress path comprised of fiber constituents (blue) and cross-links (red). The box at the critical strain, Γc, is shown in magenta. Subsequent shearing by γ is accomplished by extension of the stress path. To see this figure in color, go online.
Figure 5
The effect of connectivity, n˜X. The ensemble-averaged responses G(Γ)(A), G˜(T)(B), and G˜(T˜) (C) of networks for cross-link spring constants s→∞ (blue) and s≈4×10−5N/m (green) and connectivity n˜X≈0.12, lc≈1.2μm (circles), n˜X≈0.34, lc≈0.86μm (triangles), and n˜X≈0.72, lc≈0.34μm (squares). Standard deviations (up to about twice the symbol size) are not shown. To see this figure in color, go online.
Figure 6
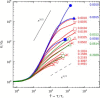
(A) Normalized initial shear modulus, G0/G0a, of the RCL network with lc=0.86μm versus characteristic ratio lb/lc, where G0a is the initial shear modulus calculated for the RCL F-actin network with μ=μa=4×10−8 N and κ=κa=6.75×10−26 N/m. The lb/lc for the RCL F-actin network is indicated by the star. Larger values of lb/lc are obtained either for μ<μa and constant κ=κa (_magenta solid symbols_) or for κ>κa and constant μ=μa (blue open symbols). The straight lines indicate the scaling laws of open-cell foams for the two extreme limits 1. (B and C) The large strain response of the RCL network for various lb/lc ratios shown in (A), where G/G0 is the network shear modulus scaled by the initial modulus, G0, and T/Tc is the stress scaled by the stress value at the onset of nonlinearity, Tc. To see this figure in color, go online.
Figure 7
View through the deformed network realization showing load-bearing supportive frames n˜X≈0.72 for the RCL limit in Fig. 5 (blue square) at T≈30Pa (A), n˜X≈0.72 for s≈4e−5N/m in Fig. 5 (green square) at T≈65Pa (B), n˜X≈0.34 for s˜=10 in Fig. 3 (red diamond) at T˜≈30 (C). The axial stress map is obtained in the same way as in Fig. 3, D_–_F. To see this figure in color, go online.
Figure 8
Compilation of all curves of G/G0 versus normalized stress, T/Tc, along with the corresponding values of l˜b/lc, for the cases in Fig. 3_C_ (where cross-link stiffness is varied at constant connectivity) and Fig. 5_C_ (at constant cross-link stiffness but varying connectivity). To see this figure in color, go online.
Similar articles
- Nonlinear Mechanics of Athermal Branched Biopolymer Networks.
Rens R, Vahabi M, Licup AJ, MacKintosh FC, Sharma A. Rens R, et al. J Phys Chem B. 2016 Jul 7;120(26):5831-41. doi: 10.1021/acs.jpcb.6b00259. Epub 2016 Mar 4. J Phys Chem B. 2016. PMID: 26901575 - Alternative explanation of stiffening in cross-linked semiflexible networks.
Onck PR, Koeman T, van Dillen T, van der Giessen E. Onck PR, et al. Phys Rev Lett. 2005 Oct 21;95(17):178102. doi: 10.1103/PhysRevLett.95.178102. Epub 2005 Oct 18. Phys Rev Lett. 2005. PMID: 16383874 - Early stiffening and softening of collagen: interplay of deformation mechanisms in biopolymer networks.
Kurniawan NA, Wong LH, Rajagopalan R. Kurniawan NA, et al. Biomacromolecules. 2012 Mar 12;13(3):691-8. doi: 10.1021/bm2015812. Epub 2012 Feb 15. Biomacromolecules. 2012. PMID: 22293015 - Continuum elastic models for force transmission in biopolymer gels.
Wang H , Xu X . Wang H , et al. Soft Matter. 2020 Dec 28;16(48):10781-10808. doi: 10.1039/d0sm01451f. Epub 2020 Dec 8. Soft Matter. 2020. PMID: 33289764 Review. - Effects of non-linearity on cell-ECM interactions.
Wen Q, Janmey PA. Wen Q, et al. Exp Cell Res. 2013 Oct 1;319(16):2481-9. doi: 10.1016/j.yexcr.2013.05.017. Epub 2013 Jun 5. Exp Cell Res. 2013. PMID: 23748051 Free PMC article. Review.
Cited by
- Effect of Fiber Crimp on the Elasticity of Random Fiber Networks With and Without Embedding Matrices.
Ban E, Barocas VH, Shephard MS, Picu CR. Ban E, et al. J Appl Mech. 2016 Apr;83(4):0410081-410087. doi: 10.1115/1.4032465. Epub 2016 Jan 27. J Appl Mech. 2016. PMID: 27222599 Free PMC article. - A structural finite element model for lamellar unit of aortic media indicates heterogeneous stress field after collagen recruitment.
Thunes JR, Pal S, Fortunato RN, Phillippi JA, Gleason TG, Vorp DA, Maiti S. Thunes JR, et al. J Biomech. 2016 Jun 14;49(9):1562-1569. doi: 10.1016/j.jbiomech.2016.03.034. Epub 2016 Apr 4. J Biomech. 2016. PMID: 27113538 Free PMC article. - The influence of physical and spatial substrate characteristics on endothelial cells.
Bjorgvinsdottir O, Ferguson SJ, Snorradottir BS, Gudjonsson T, Wuertz-Kozak K. Bjorgvinsdottir O, et al. Mater Today Bio. 2024 Apr 18;26:101060. doi: 10.1016/j.mtbio.2024.101060. eCollection 2024 Jun. Mater Today Bio. 2024. PMID: 38711934 Free PMC article. Review. - Effect of Cross-Link Homogeneity on the High-Strain Behavior of Elastic Polymer Networks.
Kong VA, Staunton TA, Laaser JE. Kong VA, et al. Macromolecules. 2024 May 8;57(10):4670-4679. doi: 10.1021/acs.macromol.3c02565. eCollection 2024 May 28. Macromolecules. 2024. PMID: 38827963 Free PMC article. - Nonlinear Actin Deformations Lead to Network Stiffening, Yielding, and Nonuniform Stress Propagation.
Gurmessa B, Ricketts S, Robertson-Anderson RM. Gurmessa B, et al. Biophys J. 2017 Oct 3;113(7):1540-1550. doi: 10.1016/j.bpj.2017.01.012. Epub 2017 Feb 16. Biophys J. 2017. PMID: 28214480 Free PMC article.
References
- Gibson L.J., Ashby M.F. 2nd ed. Cambridge University Press; Cambridge, United Kingdom: 1997. Cellular Solids.
- Picu R.C. Mechanics of random fiber networks—a review. Soft Matter. 2011;7:6768–6785.
- Bausch A.R., Kroy K. A bottom-up approach to cell mechanics. Nat. Phys. 2006;2:231–238.
- Kasza K.E., Rowat A.C., Weitz D.A. The cell as a material. Curr. Opin. Cell Biol. 2007;19:101–107. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources