Comparing the model-simulated global warming signal to observations using empirical estimates of unforced noise - PubMed (original) (raw)
Comparing the model-simulated global warming signal to observations using empirical estimates of unforced noise
Patrick T Brown et al. Sci Rep. 2015.
Abstract
The comparison of observed global mean surface air temperature (GMT) change to the mean change simulated by climate models has received much public and scientific attention. For a given global warming signal produced by a climate model ensemble, there exists an envelope of GMT values representing the range of possible unforced states of the climate system (the Envelope of Unforced Noise; EUN). Typically, the EUN is derived from climate models themselves, but climate models might not accurately simulate the correct characteristics of unforced GMT variability. Here, we simulate a new, empirical, EUN that is based on instrumental and reconstructed surface temperature records. We compare the forced GMT signal produced by climate models to observations while noting the range of GMT values provided by the empirical EUN. We find that the empirical EUN is wide enough so that the interdecadal variability in the rate of global warming over the 20(th) century does not necessarily require corresponding variability in the rate-of-increase of the forced signal. The empirical EUN also indicates that the reduced GMT warming over the past decade or so is still consistent with a middle emission scenario's forced signal, but is likely inconsistent with the steepest emission scenario's forced signal.
Figures
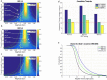
Figure 1. Steps involved in the creation of the low frequency component of the ESRUN.
(a), External radiative forcing estimates over the period of 1000–1850 broken down into components from volcanic aerosols (2 estimates), greenhouse gas concentration (1 estimate), total solar irradiance (7 estimates) and land-use albedo (2 estimates). Note that combining these forcing reconstructions yields 2×1×7×2 = 28 possible estimates of total radiative forcing over this period. (b), 15 reconstructions of surface temperature (both hemispheric and global) over the period 1000–1850 with three arbitrary reconstructions colored. (c), Estimates of the unforced component of variability over the time period (Urecon) which were obtained after Multiple Linear Regression was used to remove the forced variability from the reconstructions (see Methods). The same three arbitrary reconstructions are colored. Because there were 28 forcing estimates and 15 surface temperature estimates, there were 28×15 = 420 different Urecon estimates. (d), A sample of the low frequency component of the Urecon time series after all hemispheric estimates of unforced noise had been converted to estimates of unforced GMT noise (see Methods). The same three arbitrary reconstructions are colored. (e), The ESRUN, which combines AR(2)-simulated low frequency variability (based on the time series in panel d) with AR(2)-simulated high frequency variability based on the instrumental record (Figure S2, Methods). The grey shading in the ESRUN represents the width of the EUN at the three percentile intervals labeled in the panel. Three arbitrary realizations of GMT from the ESRUN are colored. Note that the timescale in panel e has changed because the ESRUN only needs to be 150 years long in order to study GMT change between 1900 and 2050 (Fig. 2 and Fig. 3).
Figure 2. Empirical EUN superimposed on various forced signals (black lines) over the 20th and 21st centuries.
(a), Forced signal originating from the multi-model mean of the CMIP5 ‘historical experiment' from 1900 to 2005 and RCP 6.0 from 2005 to 2013. (b), Hypothetical forced signal represented by a linear trend fit to observations during 1900 to 2013. (c), (d) and (e), Same as (a) but with forced signals corresponding to the RCP 4.5, RCP 6.0 and RCP 8.5 emissions scenarios extended to 2050. Uncertainty in the CGCM-produced forced signals is represented by ±2 standard errors calculated across all CGCM realizations (light blue shading surrounding the black line) and the EUN ranges are expanded by this uncertainty. Note that the light blue shading does not represent the uncertainty in the radiative forcings themselves but rather the uncertainty in the forced GMT signal given an assumed radiative forcing trajectory. Three arbitrary realizations of GMT from the ESRUN (superimposed on the forced signals) are shown in each panel (labeled Treali 1, Treali 2 and Treali 3). In all plots the observed GMT (as well as its 2σ uncertainty), is shown in yellow. All anomalies are defined relative to the average from 1961–1990.
Figure 3. Probabilities of observing trends of indicated lengths and magnitudes associated with the CGCM-produced forced signals incorporating the RCP 4.5, RCP 6.0 and RCP 8.5 emission scenarios.
(a), (b) and (c) show the probability of observing a linear trend of a given length and within the given magnitude bin from 1993 to 2050 as indicated by superimposing the ESRUN on the RCP 4.5, RCP 6.0 and RCP 8.5 forced signals respectively. The yellow line represents the observed trends in the GISTEMP dataset ending in 2013 and progressing backwards in time for the length of the trend (e.g., the yellow star associated with the 15-year trend length represents the linear trend from 1998 to 2013). This comparison helps indicate whether or not the observed rate of warming from 1993–2013 is consistent with the mean rate of warming from 1993–2050 expected from the 3 CGCM-produced forced signals. (d), Cancellation Timescale (see text for definition) at 0.5%, 2.5% and 5% for RCP 4.5, RCP 6.0 and RCP 8.5 (e), probability of observing at least 1 negative linear trend of the given length over the period 1993–2050 (see Methods). The red dashed line in both (d) and (e) represents the negative 11-year trend that was observed in GISTEMP from 2002 to 2013. All trends were calculated with an ordinary least squares procedure.
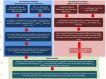
Figure 4. Flow chart illustrating the steps (labeled on the left) associated with the creation of the empirically-based Ensemble of Stochastic Realizations of Unforced Noise (ESRUN).
Steps concerning the reconstructed surface temperatures and forcings are in blue while steps concerning the surface temperatures and forcings over the instrumental era are in red. Steps dealing with combing of information from reconstructions and instrumental data are in green.
References
- Bindoff N. L., et al. Detection and Attribution of Climate Change: from Global to Regional. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. (2013).
- Hasselmann K. Stochastic climate models Part I. Theory. Tellus 28, 473–485, doi:10.1111/j.2153-3490.1976.tb00696.x (1976).
- Hawkins E. & Sutton R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bulletin of the American Meteorological Society 90, 1095–1107, 10.1175/2009BAMS2607.1 (2009). - DOI
- Brown P. T., Cordero E. C. & Mauget S. A. Reproduction of twentieth century intradecadal to multidecadal surface temperature variability in radiatively forced coupled climate models. Journal of Geophysical Research: Atmospheres 117, D11116, 10.1029/2011JD016864 (2012). - DOI
- Meehl G. A. et al. Decadal Climate Prediction: An Update from the Trenches. Bulletin of the American Meteorological Society 95, 243–267, 10.1175/BAMS-D-12-00241.1 (2013). - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous