Antisocial pool rewarding does not deter public cooperation - PubMed (original) (raw)
Antisocial pool rewarding does not deter public cooperation
Attila Szolnoki et al. Proc Biol Sci. 2015.
Abstract
Rewarding cooperation is in many ways expected behaviour from social players. However, strategies that promote antisocial behaviour are also surprisingly common, not just in human societies, but also among eusocial insects and bacteria. Examples include sanctioning of individuals who behave prosocially, or rewarding of free-riders who do not contribute to collective enterprises. We therefore study the public goods game with antisocial and prosocial pool rewarding in order to determine the potential negative consequences on the effectiveness of positive incentives to promote cooperation. Contrary to a naive expectation, we show that the ability of defectors to distribute rewards to their like does not deter public cooperation as long as cooperators are able to do the same. Even in the presence of antisocial rewarding, the spatial selection for cooperation in evolutionary social dilemmas is enhanced. Since the administration of rewards to either strategy requires a considerable degree of aggregation, cooperators can enjoy the benefits of their prosocial contributions as well as the corresponding rewards. Defectors when aggregated, on the other hand, can enjoy antisocial rewards, but due to their lack of contributions to the public good they ultimately succumb to their inherent inability to secure a sustainable future. Strategies that facilitate the aggregation of akin players, even if they seek to promote antisocial behaviour, thus always enhance the long-term benefits of cooperation.
Keywords: cooperation; evolutionary games; network reciprocity; rewarding; social dilemmas.
© 2015 The Author(s).
Figures
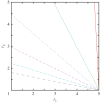
Figure 1.
In a well-mixed population, when both competing strategies are initially equally common, the extinction of rewarding cooperators is unavoidable if _r_1 < G, independently of the value of _r_2. However, if _R_C players are initially in the majority, then a new stable state emerges, where rewarding cooperators are the only players remaining in the population. In this bistable case, the border of the attractive basin depends sensitively on the initial fraction xi of _R_C players. Lines in the figure show the border of the two basins, as obtained for xi = 0.51, 0.6, 0.7, 0.8 and 0.9, from top to bottom on the _r_1−_r_2 parameter plane. The bottom-most dashed grey line shows the border in the limiting case, when there is an infinitesimally small minority of rewarding defectors initially present in the well-mixed population. (Online version in colour.)
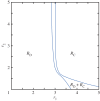
Figure 2.
Phase diagram of the studied spatial public goods game, demonstrating that the presence of antisocial rewarding does not hinder prosocial rewarding to promote cooperation. Depicted are strategies that remain on the square lattice after sufficiently long relaxation times as a function of the multiplication factor for the public goods pool _r_1 and the multiplication factor for the antisocial and prosocial rewarding pool _r_2. Solid blue lines denote continuous phase transitions. Neither cooperators (C) nor defectors (D) who abstain from participating in pool rewarding are able to survive in the stationary state. Instead, for low values of _r_1 rewarding defectors (_R_D) dominate, while for sufficiently high values of _r_1 and _r_2 rewarding cooperators (_R_C) prevail. In-between is a rather narrow two-strategy _R_D + _R_C phase, where both rewarding strategies coexist. Interestingly, for example at _r_1 = 3.5, increasing solely the value of _r_2 can lead the population from a pure _R_D to a pure _R_C phase, thus indicating clearly that rewarding, even if applied to both strategies, still promotes cooperation. (Online version in colour.)
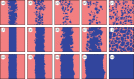
Figure 3.
Evolution of the spatial distribution of strategies over time reveals that, even in the presence of equally effective antisocial rewarding, prosocial rewarding promotes the spatial selection for cooperation in the studied public goods game. Depicted are snapshots of the square lattice over time from left to right, as obtained for (a_–_e) _r_2 = 1, (f_–_j) _r_2 = 1.3 and (k_–_o) _r_2 = 2. For clarity, we have used a prepared initial state for all cases with only a stripe of rewarding cooperators (blue) and rewarding defectors (pale red) initially present in the population, as depicted in (f). It can be observed that in the absence of rewarding (a_–_e) the interface separating the two competing strategies is broken easily, and network reciprocity alone can ultimately sustain only small cooperative clusters. However, as the effectiveness of pool rewarding increases (f_–_o), the interface is strengthened, which makes the phalanx of cooperators more effective. The latter helps to reveal the benefit of aggregated cooperators in structured populations. In all three cases, the synergy factor for the main public goods game is _r_1 = 3.8. (Online version in colour.)
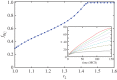
Figure 4.
Quantitative evidence in support of enhanced spatial selection for cooperation in the studied spatial public goods game with antisocial and prosocial pool rewarding. The inset shows early stages of the evolution of the width w of the mixed zone, where both strategies are present after initially starting from a prepared initial state, as depicted in figure 3_f_. From top to bottom, the curves were obtained for _r_2 = 1, 1.1, 1.2, 1.3, 1.4, 1.5 and 2, and they correspond to the average over 100 independent runs at system size L × L = 100 × 100. In all cases, the synergy factor for the main public goods game is _r_1 = 3.8. The main panel shows the corresponding increase in the fraction of rewarding cooperators  as _r_2 increases, thus indicating that the favourable outcome is indeed due to the enhanced stability of interfaces in structured populations. This enables cooperators to dominate completely even at low values of _r_1, where in well-mixed populations they would not be able to survive, and where based only on network reciprocity they would fare poorly. (Online version in colour.)
as _r_2 increases, thus indicating that the favourable outcome is indeed due to the enhanced stability of interfaces in structured populations. This enables cooperators to dominate completely even at low values of _r_1, where in well-mixed populations they would not be able to survive, and where based only on network reciprocity they would fare poorly. (Online version in colour.)
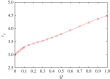
Figure 5.
Random rewiring enables defectors to enjoy the benefits of antisocial rewarding and free-riding on the cooperative efforts of others, but relatively healthy conditions for the evolution of cooperation are maintained even if the randomness of the interaction network is high. Depicted is the critical value of _r_1 = _r_c at which the population arrives to a pure _R_D phase. It can be observed that _r_c-values increase steadily as Q increases, yet stay below the survival threshold of cooperators in a well-mixed population even at Q = 1. The synergy factor for the antisocial and prosocial pool rewarding scheme is _r_2 = 2. Qualitatively identical results are obtained also for other values of _r_2. (Online version in colour.)
Similar articles
- Antisocial rewarding in structured populations.
Dos Santos M, Peña J. Dos Santos M, et al. Sci Rep. 2017 Jul 24;7(1):6212. doi: 10.1038/s41598-017-06063-9. Sci Rep. 2017. PMID: 28740243 Free PMC article. - The evolution of anti-social rewarding and its countermeasures in public goods games.
dos Santos M. dos Santos M. Proc Biol Sci. 2015 Jan 7;282(1798):20141994. doi: 10.1098/rspb.2014.1994. Proc Biol Sci. 2015. PMID: 25429015 Free PMC article. - Antisocial peer exclusion does not eliminate the effectiveness of prosocial peer exclusion in structured populations.
Li S, Du C, Li X, Shen C, Shi L. Li S, et al. J Theor Biol. 2024 Jan 7;576:111665. doi: 10.1016/j.jtbi.2023.111665. Epub 2023 Nov 10. J Theor Biol. 2024. PMID: 37951564 - Review: Game theory of public goods in one-shot social dilemmas without assortment.
Archetti M, Scheuring I. Archetti M, et al. J Theor Biol. 2012 Apr 21;299:9-20. doi: 10.1016/j.jtbi.2011.06.018. Epub 2011 Jun 24. J Theor Biol. 2012. PMID: 21723299 Review. - On the interaction of the stick and the carrot in social dilemmas.
Milinski M, Rockenbach B. Milinski M, et al. J Theor Biol. 2012 Apr 21;299:139-43. doi: 10.1016/j.jtbi.2011.03.014. Epub 2011 Mar 31. J Theor Biol. 2012. PMID: 21458464 Review.
Cited by
- Knowing the past improves cooperation in the future.
Danku Z, Perc M, Szolnoki A. Danku Z, et al. Sci Rep. 2019 Jan 22;9(1):262. doi: 10.1038/s41598-018-36486-x. Sci Rep. 2019. PMID: 30670732 Free PMC article. - Risk-aware multi-armed bandit problem with application to portfolio selection.
Huo X, Fu F. Huo X, et al. R Soc Open Sci. 2017 Nov 15;4(11):171377. doi: 10.1098/rsos.171377. eCollection 2017 Nov. R Soc Open Sci. 2017. PMID: 29291122 Free PMC article. - Self-serving reward and punishment: evidence from the laboratory.
Chen J, Lian Z, Zheng J. Chen J, et al. Sci Rep. 2023 Aug 26;13(1):13997. doi: 10.1038/s41598-023-41256-5. Sci Rep. 2023. PMID: 37634044 Free PMC article. - Cooperation enhanced by the coevolution of teaching activity in evolutionary prisoner's dilemma games with voluntary participation.
Shen C, Chu C, Geng Y, Jin J, Chen F, Shi L. Shen C, et al. PLoS One. 2018 Feb 16;13(2):e0193151. doi: 10.1371/journal.pone.0193151. eCollection 2018. PLoS One. 2018. PMID: 29451899 Free PMC article. - Combination of institutional incentives for cooperative governance of risky commons.
Sun W, Liu L, Chen X, Szolnoki A, Vasconcelos VV. Sun W, et al. iScience. 2021 Jul 12;24(8):102844. doi: 10.1016/j.isci.2021.102844. eCollection 2021 Aug 20. iScience. 2021. PMID: 34381969 Free PMC article.
References
- Ostrom E. 1990. Governing the commons: the evolution of institutions for collective action. Cambridge, UK: Cambridge University Press.
- Wu Z-X, Rong Z, Chen MZQ. 2015. Diverse roles of the reduced learning ability of players in the evolution of cooperation. EPL 110, 30002 (10.1209/0295-5075/110/30002) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources