Intuition, deliberation, and the evolution of cooperation - PubMed (original) (raw)
Intuition, deliberation, and the evolution of cooperation
Adam Bear et al. Proc Natl Acad Sci U S A. 2016.
Abstract
Humans often cooperate with strangers, despite the costs involved. A long tradition of theoretical modeling has sought ultimate evolutionary explanations for this seemingly altruistic behavior. More recently, an entirely separate body of experimental work has begun to investigate cooperation's proximate cognitive underpinnings using a dual-process framework: Is deliberative self-control necessary to reign in selfish impulses, or does self-interested deliberation restrain an intuitive desire to cooperate? Integrating these ultimate and proximate approaches, we introduce dual-process cognition into a formal game-theoretic model of the evolution of cooperation. Agents play prisoner's dilemma games, some of which are one-shot and others of which involve reciprocity. They can either respond by using a generalized intuition, which is not sensitive to whether the game is one-shot or reciprocal, or pay a (stochastically varying) cost to deliberate and tailor their strategy to the type of game they are facing. We find that, depending on the level of reciprocity and assortment, selection favors one of two strategies: intuitive defectors who never deliberate, or dual-process agents who intuitively cooperate but sometimes use deliberation to defect in one-shot games. Critically, selection never favors agents who use deliberation to override selfish impulses: Deliberation only serves to undermine cooperation with strangers. Thus, by introducing a formal theoretical framework for exploring cooperation through a dual-process lens, we provide a clear answer regarding the role of deliberation in cooperation based on evolutionary modeling, help to organize a growing body of sometimes-conflicting empirical results, and shed light on the nature of human cognition and social decision making.
Keywords: cooperation; dual process; evolutionary game theory; heuristics; prisoner's dilemma.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
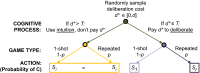
Fig. 1.
Agents play PD games that are either one-shot or involve reciprocity, and either use a generalized intuitive strategy that does not depend on game type, or engage in costly deliberation and tailor their strategy based on game type. The strategy space for the agents in our model, which consists of four variables T, _S_i, _S_1, and _S_r, is visualized here along with the sequence of events within each interaction between two agents (both agents face the same decision, so for illustrative simplicity only one agent’s decision process is shown). First, the agent’s cost of deliberation for this interaction d* is sampled uniformly from the interval [0, _d_]. The agent’s deliberation threshold T then determines which mode of cognitive processing is applied. If d* > T, it is too costly to deliberate in this interaction and she makes her cooperation decision based on her generalized intuitive response S_i; intuition cannot differentiate between game types, and so regardless of whether the game is one-shot (probability 1−_p) or repeated (probability p), she plays the cooperative strategy with probability _S_i. If d* ≤ T, however, deliberation is not too costly, so she pays the cost d* and uses deliberation to tailor her play to the type of game she is facing: If the game is one-shot, she plays the cooperative strategy with probability _S_1, and if the game is repeated, she plays the cooperative strategy with probability _S_r. For example, when deliberating, an agent could decide to defect in a one-shot game (_S_1 = 0) but cooperate in a repeated game (_S_r = 1). In contrast, when using intuition, this agent must either cooperate in both contexts (_S_i = 1) or defect in both contexts (_S_i = 0).
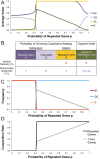
Fig. 2.
Reciprocity leads evolution to favor dual-process agents who intuitively cooperate but use deliberation to defect in one-shot games. (A) Shown are the average values of each strategy variable in the steady-state distribution of the evolutionary process, as a function of the probability of repeated games p. When most interactions are one-shot (p is small), agents intuitively defect (_S_i = 0) and rarely deliberate (_T_∼0) (as a result, the deliberative cooperation strategies for one-shot games _S_1 and repeated games _S_r are rarely used, and so their values are dominated by neutral drift and sit near 0.5). Conversely, when the probability of repeated games (i.e., the extent of reciprocity) is sufficiently high (p > 0.3 for these parameters), agents evolve to be intuitively cooperative (_S_i = 1) and to pay substantial costs to deliberate (T >> 0); and when these agents deliberate, they cooperate in repeated games (_S_r = 1) and defect in one-shot games (_S_1 = 0). As the probability of repeated games p increases beyond this point, these intuitive and deliberative responses do not change, but agents become less willing to deliberate (T decreases). Evolutionary calculations use N = 50, b = 4, c = 1, d = 1, w = 6, and a = 0; see SI Appendix, Fig. S2 for calculations using other parameter values. (B) To better understand the dynamics in A, we perform Nash equilibrium calculations. There are two possible equilibria, which are described here: (i) the ID strategy, which never deliberates (T = 0) and always intuitively defects (_S_i = 0; _S_1 and _S_r are undefined because deliberation is never used); and (ii) the DC strategy, which intuitively cooperates (S_i = 1) and is willing to pay a maximum cost of T = c(1−_p) to deliberate, in which case it cooperates in repeated games (_S_r = 1) and switches to defection in one-shot games (_S_1 = 0). (C) Evolutionary calculations using only these two strategies successfully reproduce the results of the full strategy space in A. Thus, these two strategies are sufficient to characterize the dynamics of the system: We find that the population shifts from entirely ID to entirely DC once p becomes large enough for DC to risk-dominate ID (see SI Appendix for calculation details). (D) As a result, cooperation in repeated games goes to ceiling as soon as p passes this threshold, whereas cooperation in one-shot games slowly increases with p.
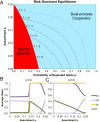
Fig. 3.
Assortment also favors the evolution of dual process cooperators. (A) Nash equilibrium calculations with assortment (a > 0) again find that ID and DC are the only possible equilibria. The risk-dominant strategy is shown as a function of the probability of repeated games p and the level of assortment a (risk-dominance indicates which strategy will be favored by selection; see SI Appendix, Fig. S1 for corresponding evolutionary calculations). DC is favored so long as either p or a are sufficiently large. Thus, regardless of whether evolution occurs in a world where reciprocity is powerful and assortment is weak, or where reciprocity is weak and assortment is strong, selection favors intuitive cooperation combined with deliberative defection in one-shot games. Also shown are isoclines for T within the region where DC is favored. Here, increasing either a or p decreases T. Thus, we find an interaction with reciprocity when considering how assortment affects cognitive style: when p is low, assortment initially increases deliberation, but when p is high, assortment monotonically decreases deliberation. This interaction is visualized by showing the average values of each strategy variable in the steady-state distribution of the evolutionary process as a function of assortment a, for p = 0.2 (B) and p = 0.6 (C). Evolutionary calculations use N = 50, b = 4, c = 1, d = 1, and w = 6.
Comment in
- Models inconsistent with altruism cannot explain the evolution of human cooperation.
Myrseth KO, Wollbrant CE. Myrseth KO, et al. Proc Natl Acad Sci U S A. 2016 May 3;113(18):E2472. doi: 10.1073/pnas.1602463113. Epub 2016 Apr 18. Proc Natl Acad Sci U S A. 2016. PMID: 27091958 Free PMC article. No abstract available. - Reply to Myrseth and Wollbrant: Our model is consistent with altruism, and helps to explain its evolution.
Bear A, Rand DG. Bear A, et al. Proc Natl Acad Sci U S A. 2016 May 3;113(18):E2473. doi: 10.1073/pnas.1603854113. Epub 2016 Apr 18. Proc Natl Acad Sci U S A. 2016. PMID: 27092010 Free PMC article. No abstract available.
Similar articles
- Population Structure Promotes the Evolution of Intuitive Cooperation and Inhibits Deliberation.
Mosleh M, Rand DG. Mosleh M, et al. Sci Rep. 2018 Apr 19;8(1):6293. doi: 10.1038/s41598-018-24473-1. Sci Rep. 2018. PMID: 29674677 Free PMC article. - Cooperation, Fast and Slow: Meta-Analytic Evidence for a Theory of Social Heuristics and Self-Interested Deliberation.
Rand DG. Rand DG. Psychol Sci. 2016 Sep;27(9):1192-206. doi: 10.1177/0956797616654455. Epub 2016 Jul 15. Psychol Sci. 2016. PMID: 27422875 - Co-evolution of cooperation and cognition: the impact of imperfect deliberation and context-sensitive intuition.
Bear A, Kagan A, Rand DG. Bear A, et al. Proc Biol Sci. 2017 Mar 29;284(1851):20162326. doi: 10.1098/rspb.2016.2326. Proc Biol Sci. 2017. PMID: 28330915 Free PMC article. - Why humans might help strangers.
Raihani NJ, Bshary R. Raihani NJ, et al. Front Behav Neurosci. 2015 Feb 20;9:39. doi: 10.3389/fnbeh.2015.00039. eCollection 2015. Front Behav Neurosci. 2015. PMID: 25750619 Free PMC article. Review. - Resolving the iterated prisoner's dilemma: theory and reality.
Raihani NJ, Bshary R. Raihani NJ, et al. J Evol Biol. 2011 Aug;24(8):1628-39. doi: 10.1111/j.1420-9101.2011.02307.x. Epub 2011 May 23. J Evol Biol. 2011. PMID: 21599777 Review.
Cited by
- Vaccinating SIS epidemics under evolving perception in heterogeneous networks.
Li XJ, Li X. Li XJ, et al. Eur Phys J B. 2020;93(10):185. doi: 10.1140/epjb/e2020-10355-3. Epub 2020 Oct 5. Eur Phys J B. 2020. PMID: 33024413 Free PMC article. - Think global, act local: Preserving the global commons.
Hauser OP, Hendriks A, Rand DG, Nowak MA. Hauser OP, et al. Sci Rep. 2016 Nov 3;6:36079. doi: 10.1038/srep36079. Sci Rep. 2016. PMID: 27808222 Free PMC article. - Adaptations to infer fitness interdependence promote the evolution of cooperation.
Colnaghi M, Santos FP, Van Lange PAM, Balliet D. Colnaghi M, et al. Proc Natl Acad Sci U S A. 2023 Dec 12;120(50):e2312242120. doi: 10.1073/pnas.2312242120. Epub 2023 Dec 6. Proc Natl Acad Sci U S A. 2023. PMID: 38055736 Free PMC article. - Coevolution between the cost of decision and the strategy contributes to the evolution of cooperation.
Ohdaira T. Ohdaira T. Sci Rep. 2019 Mar 14;9(1):4465. doi: 10.1038/s41598-019-41073-9. Sci Rep. 2019. PMID: 30872729 Free PMC article. - Electrophysiological Markers of Fairness and Selfishness Revealed by a Combination of Dictator and Ultimatum Games.
Miraghaie AM, Pouretemad H, Villa AEP, Mazaheri MA, Khosrowabadi R, Lintas A. Miraghaie AM, et al. Front Syst Neurosci. 2022 May 9;16:765720. doi: 10.3389/fnsys.2022.765720. eCollection 2022. Front Syst Neurosci. 2022. PMID: 35615426 Free PMC article.
References
- Rand DG, Nowak MA. Human cooperation. Trends Cogn Sci. 2013;17(8):413–425. - PubMed
- Bowles S, Gintis H. Prosocial emotions. In: Blume LE, Durlauf SN, editors. The Economy as an Evolving Complex System 3. Oxford Univ Press; Oxford: 2002. pp. 339–364.
- Small DA, Loewenstein G, Slovic P. Sympathy and callousness: The impact of deliberative thought on donations to identifiable and statistical victims. Organ Behav Hum Decis Process. 2007;102(2):143–153.
- Rand DG, Greene JD, Nowak MA. Spontaneous giving and calculated greed. Nature. 2012;489(7416):427–430. - PubMed
- Zaki J, Mitchell JP. Intuitive Prosociality. Curr Dir Psychol Sci. 2013;22(6):466–470.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources