FINEMAP: efficient variable selection using summary data from genome-wide association studies - PubMed (original) (raw)
FINEMAP: efficient variable selection using summary data from genome-wide association studies
Christian Benner et al. Bioinformatics. 2016.
Abstract
Motivation: The goal of fine-mapping in genomic regions associated with complex diseases and traits is to identify causal variants that point to molecular mechanisms behind the associations. Recent fine-mapping methods using summary data from genome-wide association studies rely on exhaustive search through all possible causal configurations, which is computationally expensive.
Results: We introduce FINEMAP, a software package to efficiently explore a set of the most important causal configurations of the region via a shotgun stochastic search algorithm. We show that FINEMAP produces accurate results in a fraction of processing time of existing approaches and is therefore a promising tool for analyzing growing amounts of data produced in genome-wide association studies and emerging sequencing projects.
Availability and implementation: FINEMAP v1.0 is freely available for Mac OS X and Linux at http://www.christianbenner.com
Contact: : christian.benner@helsinki.fi or matti.pirinen@helsinki.fi.
© The Author 2016. Published by Oxford University Press.
Figures
Fig. 1.
The binary indicator vector γ determines which SNPs have non-zero causal effects (
). The corresponding causal (linear) model for a quantitative trait assumes only few SNPs with a causal effect. The Maximum Likelihood Estimate (MLE) of the causal SNP effects λˆ can be computed by using only the SNP correlation matrix and single-SNP _z_-scores. However, the MLE is not ideal because it does not account for the sparsity assumption
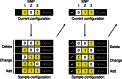
Fig. 2.
Shotgun stochastic search rapidly identifies configurations of causal SNPs with high posterior probability. In each iteration, the neighborhood of the current causal configuration is defined by configurations that result from deleting, changing or adding a causal SNP () from the current configuration. The next iteration starts by sampling a new causal configuration from the neighborhood based on the scores normalized within the neighborhood. The unnormalized posterior probabilities remain fixed throughout the algorithm and can thus be memorized (
) to avoid recomputation when already-evaluated configurations appear in another neighborhood
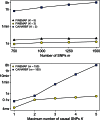
Fig. 3.
Processing time of one locus with FINEMAP and CAVIARBF on log10 scale. Top panel: Scenario A with increasing number of SNPs allowing K = 3 or K = 5 causal SNPs. Bottom panel: Scenario B with 150 SNPs considering causal configurations with different maximum numbers of SNPs. All processing times are averaged over 500 datasets using one core of a Intel Haswell E5-2690v3 processor running at 2.6 GHz
Fig. 4.
Single-SNP inclusion probabilities of all SNPs in Scenario B with absolute difference larger than 0.01 between FINEMAP and CAVIARBF
Fig. 5.
Fine-mapping accuracy of FINEMAP and CAVIARBF on data with five causal SNPs, allowing either K = 3 or K = 5 causal SNPs. The proportion of causal SNPs included is plotted against the number of top SNPs selected on the basis of ranked single-SNP inclusion probabilities. Proportions are averaged over 500 datasets with 1500 SNPs. Case K = 5 is computationally intractable for CAVIARBF
Fig. 6.
Fine-mapping of 4q22/SNCA region associated with Parkinson’s disease. Associated SNPs rs356220 and rs7687945 are highlighted by 
and their configuration by 
. Dashed lines correspond respectively to a single-SNP Bayes factor of 100 and _P_-value of 5×10−8. Squared correlations are shown with respect to rs356220
Fig. 7.
Fine-mapping of 15q21/LIPC region associated with high-density lipoprotein cholesterol. Independent association signals in conditional analysis are highlighted by . Dashed lines correspond respectively to a single-SNP Bayes factor of 100 and _P_-value of 5×10−8. Squared correlations are shown with respect to rs2043085
References
- Andrieu C. et al. (2003) An introduction to MCMC for machine learning. Mach. Learn., 50, 5–43.
- Bottolo L., Richardson S. (2010) Evolutionary stochastic search for Bayesian model exploration. Bayesian Anal., 3, 583–618.
- Borodulin K. et al. (2015) Forty-year trends in cardiovascular risk factors in Finland. Eur. J. Public Health, 25, 539–546. - PubMed
- Carbonetto P., Stephens M. (2012) Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal., 1, 73–108.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources