α-Actinin links extracellular matrix rigidity-sensing contractile units with periodic cell-edge retractions - PubMed (original) (raw)

. 2016 Nov 7;27(22):3471-3479.

doi: 10.1091/mbc.E16-02-0107. Epub 2016 Apr 27.

Haguy Wolfenson 1, Shuaimin Liu 3, Matthew R Stachowiak 2, Thomas Iskratsch 4 5, Anurag Mathur 3, Saba Ghassemi 3, Nils Gauthier 4 6, Erdem Tabdanov 7, James Lohner 4, Alexander Gondarenko 3, Ashok C Chander 4, Pere Roca-Cusachs 4 8, Ben O'Shaughnessy 2, James Hone 3, Michael P Sheetz 1 6

Affiliations

Giovanni Meacci et al. Mol Biol Cell. 2016.

Abstract

During spreading and migration, the leading edges of cells undergo periodic protrusion-retraction cycles. The functional purpose of these cycles is unclear. Here, using submicrometer polydimethylsiloxane pillars as substrates for cell spreading, we show that periodic edge retractions coincide with peak forces produced by local contractile units (CUs) that assemble and disassemble along the cell edge to test matrix rigidity. We find that, whereas actin rearward flow produces a relatively constant force inward, the peak of local contractile forces by CUs scales with rigidity. The cytoskeletal protein α-actinin is shared between these two force-producing systems. It initially localizes to the CUs and subsequently moves inward with the actin flow. Knockdown of α-actinin causes aberrant rigidity sensing, loss of CUs, loss of protrusion-retraction cycles, and, surprisingly, enables the cells to proliferate on soft matrices. We present a model based on these results in which local CUs drive rigidity sensing and adhesion formation.

© 2016 Meacci, Wolfenson, et al. This article is distributed by The American Society for Cell Biology under license from the author(s). Two months after publication it is available to the public under an Attribution–Noncommercial–Share Alike 3.0 Unported Creative Commons License (http://creativecommons.org/licenses/by-nc-sa/3.0).

PubMed Disclaimer

Figures

FIGURE 1:

FIGURE 1:

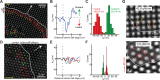
Local contractions of the matrix under the cell edge during cell spreading. (A) Typical map of pillar deflections under an isotropically spreading MEF 20 min after plating showing periodic protrusion–retractions. Local contractions involve inward deflections at the leading edge (red arrows) and outward deflections 2–3 μm behind (green arrows). Displacements are shown for pillars that were outside the cell at t = 0 s and that had displacements at least fivefold (red arrows) and twofold (green arrows) greater than the average noise (6 nm). Additionally, arrows in and around the nuclear region that were inside the cell at t = 0 s are displayed to illustrate the randomly directed displacements under the cell nucleus and the presence of a region between the leading edge and the nuclear region with no significant displacements. White arrow: direction of leading edge extension. Yellow arrow at the top corresponds to 60 nm displacement. (B) Representative trace of a single pillar deflection (stiffness = 13.9 pN/nm) in the direction of the cell motion as a function of distance behind the cell’s leading edge. Because displacements were primarily in the direction perpendicular to the cell edge, only the component of the displacement in this direction, _d_⊥, was plotted. (C) Histograms of maximum outward (green) and inward (red) displacements of pillars with respect to the direction of the cell motion. Differences between inward and outward displacements were significant (n = 68 pillars, p < 0.001, Mann-Whitney rank-sum test). (D–F) Control experiment on ultrastiff pillars (690 pN/nm): (D) map of pillar deflections under an isotropically spreading cell 20 min after plating. White arrow: direction of leading edge extension. Yellow arrow at the bottom corresponds to 60 nm displacement; (E) three representative traces of single-pillar deflection in the direction of cell motion, _d_⊥, as a function of distance behind the cell’s leading edge; (F) histograms of maximum outward (green) and inward (red) displacements of pillars with respect to the direction of the cell motion for ultrastiff pillars (n = 52 pillars from 3 cells). Maximum outward: 9 ± 4 nm; maximum inward: −17 ± 4 nm. (G) Examples of pillar-displacement vectors on stiff (43.6 pN/nm) and ultrasoft (0.8 pN/Nm) pillars.

FIGURE 2:

FIGURE 2:

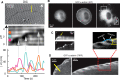
α-Actinin localization correlates with protrusion–retraction cycles of the cell edge. (A) Pillar displacement correlates with periodic leading-edge retractions. Top, DIC image of an MEF spreading on PDMS pillars coated with FN (10 μg/ml). White arrow, cell spreading direction. Middle, kymograph from the pillar row indicated in yellow in the DIC image. White horizontal streaks are the pillars; the black streak is the cell’s leading edge. Arrows indicate the pillar centers at the times the peaks reach their maximum. Bottom, displacement as a function of time for three pillars in the kymograph, indicated by dots with the same color as the corresponding displacement line. (B) Images from a video taken by epifluorescence microscopy of a GFP-α-actinin–expressing cell spreading on FN-coated glass (10 μg/ml). (C) Top, kymograph taken from box 1 in the right image in B; arrow indicates the point in time of α-actinin removal from the edge, which coincides with dissipation of the protrusion–retraction cycles. Bottom, kymograph taken from box 2 (rotated 90° to the left) in the right image in B. (D) Left, TIRF image of a GFP-α-actinin–expressing cell after 20 min spreading on FN-coated glass (10 μg/ml). Middle, kymograph obtained from the video associated with the image on the left. Right, zoom from the red square highlighted in the middle image. The distribution of α-actinin attains its largest width perpendicular to the leading edge during the onset of the retraction phase.

FIGURE 3:

FIGURE 3:

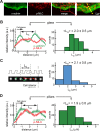
Myosin II and α-actinin form contractile units. (A) Fluorescence images of GFP-α-actinin and Alexa Fluor 555 anti p-MLC of a cell spread for 25 min. (B) Left, average profiles of α-actinin and anti p-MLC obtained from multiple positions along the edges of cells plated on FN-coated glass at regions undergoing retraction (see, e.g., the yellow dashed line in A, right); right, histogram of the α-actinin peak-to-peak distance, _L_α, as defined on the left (6 cells, n = 71 profiles). (C) Left, the contractile unit length, _L_c, was defined for each row of pillars perpendicular to the leading edge as the separation between the two pillars showing over time the largest product of the components of inward and outward deflections along the row axis. Deflections were filtered in time with a 5-point moving average. Right, histogram of the contractile unit length, _L_c (n = 47 rows of pillars, 238 pillars, 3 cells). (D) Left, average profiles of α-actinin and anti p-MLC obtained from the average of multiple positions along the edge of multiple cells plated on FN-coated pillars at regions undergoing retraction; right, histogram of the α-actinin peak-to-peak distance, _L_α, as defined on the left (n = 90 profiles).

FIGURE 4:

FIGURE 4:

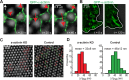
α-Actinin’s effect on CUs and rigidity sensing. (A) Time-lapse images of a live cell showing the displacement map and GFP-α-actinin localization (3B analysis). α-Actinin concentrates on the inside half of the pillar at the time of peak inward displacement. Displacements are shown only for pillars that were outside the cell at t = 0 s and above the noise. The vertical white arrow represents spreading direction. The adhesion complexes initially form around the edges of the pillars, because these are the first points of contact of the cell edge with the matrix when the former is protruding forward. (B) Images taken from Supplemental Video S7 showing initial recruitment of GFP-α-actinin around the pillars, followed by its retraction back toward the cell center, resulting in an elongated pattern. (C) Typical map of pillar deflections under a spreading MEF 20–25 min after plating. Displacements are shown only for pillars that were outside the cell at t = 0 s and that had displacements greater than 15 nm for the inward deflection (red arrows) and 20 nm for the outward deflections (green arrows). Left, cells were transfected with α-actinin short hairpin RNA (shRNA). Only inward deflections at the leading edge (red arrows) are observed. Right, cells were transfected with control shRNA. Local contractions involve inward deflections at the leading edge (red arrows) and outward deflections 2–3 μm behind (green arrows). (D) Histograms of maximum displacements, |d|max. Differences between α-actinin shRNA cells (left) and control cells (right) were significant (left: n = 51 pillars for 4 cells; right: n = 243 for 5 cells; p < 0.001, Mann-Whitney rank-sum test). Errors are given by the SD (pillar stiffness = 13.9 pN/nm).

FIGURE 5:

FIGURE 5:

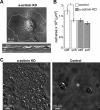
α-Actinin depletion affects rigidity sensing. (A) Top, image taken from a video of an α-actinin-KD cell spreading on FN-coated glass; bottom, kymograph from the black line in the top image showing periodic instances of cell-edge protrusions followed by complete retraction to approximately the starting positions. (B) Average area of cells transfected with control and α-actinin shRNA after 1 h of spreading on stiff and soft pillars (n > 30 in all cases). *, p < 0.01, Student’s t test. (C) DIC images of control and α-actinin KD cells after 3 d in culture on 0.2 kPa gels.

FIGURE 6:

FIGURE 6:

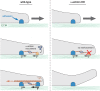
Model for α-actinin’s role in rigidity sensing. Left, rigidity sensing in the presence of α-actinin. When the cell edge protrudes forward (top), it forms new contact with the matrix (orange dome in middle panel); this triggers the formation of CUs that apply contractile forces on neighboring adhesions, which requires the recruitment of α-actinin to reinforce adhesions (typical distance between the adhesions within a CU is ∼2 μm). Subsequently the lamellipodial network (actin flow) applies pulling centripetal forces on the adhesions (bottom). Right, aberrant rigidity sensing in the absence of α-actinin. When the initial contractions occur, and no α-actinin is present to reinforce the adhesions (middle), they eventually break (bottom), resulting in ruffling of the cell edge. Ruffling also occurs in wild-type cells on soft matrices when α-actinin–mediated adhesion reinforcement does not occur and adhesions break (Wolfenson et al., 2016).

Similar articles

Cited by

References

    1. Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. - PubMed
    1. Chen L, Vicente-Manzanares M, Potvin-Trottier L, Wiseman PW, Horwitz AR. The integrin-ligand interaction regulates adhesion and migration through a molecular clutch. PLoS One. 2012;7:e40202. - PMC - PubMed
    1. Choi CK, Vicente-Manzanares M, Zareno J, Whitmore LA, Mogilner A, Horwitz AR. Actin and alpha-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat Cell Biol. 2008;10:1039–1050. - PMC - PubMed
    1. Cox S, Rosten E, Monypenny J, Jovanovic-Talisman T, Burnette DT, Lippincott-Schwartz J, Jones GE, Heintzmann R. Bayesian localization microscopy reveals nanoscale podosome dynamics. Nat Methods. 2012;9:195–200. - PMC - PubMed
    1. Dobereiner HG, Dubin-Thaler B, Giannone G, Xenias HS, Sheetz MP. Dynamic phase transitions in cell spreading. Phys Rev Lett. 2004;93:108105. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources