Evolution of cooperation by the introduction of the probabilistic peer-punishment based on the difference of payoff - PubMed (original) (raw)
Evolution of cooperation by the introduction of the probabilistic peer-punishment based on the difference of payoff
Tetsushi Ohdaira. Sci Rep. 2016.
Abstract
There are two types of costly punishment, i.e. peer-punishment and pool-punishment. While peer-punishment applies direct face to face punishment, pool-punishment is based on multi-point, collective interaction among group members. Regarding those two types of costly punishment, peer-punishment is especially considered to have the flaws that it lowers the average payoff of all players as well as pool-punishment does, and facilitates antisocial behaviour like retaliation of a defector on a cooperator. Here, this study proposes the new peer-punishment that punishment to an opponent player works at high probability when an opponent one is uncooperative, and the difference of payoff between a player and an opponent one becomes large in order to prevent such antisocial behaviour. It is natural to think that players of high payoff do not expect to punish others of lower payoff because they do not have any complaints regarding their economic wealth. The author shows that the introduction of the proposed peer-punishment increases both the number of cooperative players and the average payoff of all players in various types of topology of connections between players.
Figures
Figure 1. The sample initial state of the regular topology of connections of <_k_> = 4.
The regular topology of connections means that the number of players having connections with player i (k(i)) is the same regarding all players. The spatial structure of connections is defined as the one dimensional lattice of periodic boundary conditions, and each vertex of the lattice exhibits each player. Note that this figure has only twenty players (N = 20) in order to make clear the spatial structure of connections. The ratio of the number of defectors (red) to the number of cooperators (blue) approximately equals one to one, and defectors and cooperators are randomly distributed in every simulation run. Each type of the topology of connections in each initial state does not change during every simulation run.
Figure 2
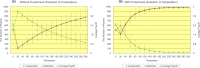
The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the regular topology of connections of <_k_> = 4 (a) without/(b) with the proposed peer-punishment. Note that error bars are SD (standard deviation).
Figure 3
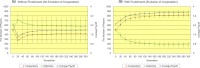
The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the random topology of connections of <_k_> = 4 (a) without/(b) with the proposed peer-punishment. Note that error bars are SD (standard deviation).
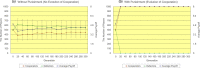
Figure 4. The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the scale-free topology of connections of <_k_> = 4.
Regarding the case without the proposed peer-punishment, the panel (a) shows the case where the number of defectors increases (14/20 simulation runs), while the panel (b) shows the case where the number of cooperators increases (6/20 simulation runs). Regarding the case with the proposed peer-punishment (c), the number of cooperators increases in all simulation runs. Note that error bars are SD (standard deviation).
Figure 5. The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the regular topology of connections of = 8.
The panel (a) shows the result of the increase in the number of defectors without the proposed peer-punishment (17/20 simulation runs), while the panel (b) shows the result of the increase in the number of cooperators with the proposed peer-punishment (all simulation runs). Note that error bars are SD (standard deviation).
Figure 6
The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the random topology of connections of <_k_> = 8 (a) without/(b) with the proposed peer-punishment. Note that error bars are SD (standard deviation).
Figure 7. The time series results of the number of defectors (left vertical axis), the number of cooperators (left vertical axis), and the average payoff of all players (right vertical axis) regarding the scale-free topology of connections of <_k_> = 8.
Regarding the case without the proposed peer-punishment, the panel (a) shows the case where the number of defectors increases (17/20 simulation runs), while the panel (b) shows the case where the number of cooperators increases (3/20 simulation runs). Regarding the case with the proposed peer-punishment (c), the number of cooperators increases in all simulation runs. Note that error bars are SD (standard deviation).
Similar articles
- The probabilistic pool punishment proportional to the difference of payoff outperforms previous pool and peer punishment.
Ohdaira T. Ohdaira T. Sci Rep. 2022 Apr 22;12(1):6604. doi: 10.1038/s41598-022-10582-5. Sci Rep. 2022. PMID: 35459880 Free PMC article. - A remarkable effect of the combination of probabilistic peer-punishment and coevolutionary mechanism on the evolution of cooperation.
Ohdaira T. Ohdaira T. Sci Rep. 2017 Sep 29;7(1):12448. doi: 10.1038/s41598-017-12742-4. Sci Rep. 2017. PMID: 28963526 Free PMC article. - Effect of the presence of empty sites on the evolution of cooperation by costly punishment in spatial games.
Sekiguchi T, Nakamaru M. Sekiguchi T, et al. J Theor Biol. 2009 Jan 21;256(2):297-304. doi: 10.1016/j.jtbi.2008.09.025. Epub 2008 Oct 10. J Theor Biol. 2009. PMID: 18952110 - On the interaction of the stick and the carrot in social dilemmas.
Milinski M, Rockenbach B. Milinski M, et al. J Theor Biol. 2012 Apr 21;299:139-43. doi: 10.1016/j.jtbi.2011.03.014. Epub 2011 Mar 31. J Theor Biol. 2012. PMID: 21458464 Review. - Punishment: one tool, many uses.
Raihani NJ, Bshary R. Raihani NJ, et al. Evol Hum Sci. 2019 Nov 12;1:e12. doi: 10.1017/ehs.2019.12. eCollection 2019. Evol Hum Sci. 2019. PMID: 37588410 Free PMC article. Review.
Cited by
- Cooperation without punishment.
Battu B, Rahwan T. Battu B, et al. Sci Rep. 2023 Jan 21;13(1):1213. doi: 10.1038/s41598-023-28372-y. Sci Rep. 2023. PMID: 36681708 Free PMC article. - The probabilistic pool punishment proportional to the difference of payoff outperforms previous pool and peer punishment.
Ohdaira T. Ohdaira T. Sci Rep. 2022 Apr 22;12(1):6604. doi: 10.1038/s41598-022-10582-5. Sci Rep. 2022. PMID: 35459880 Free PMC article. - Coevolution between the cost of decision and the strategy contributes to the evolution of cooperation.
Ohdaira T. Ohdaira T. Sci Rep. 2019 Mar 14;9(1):4465. doi: 10.1038/s41598-019-41073-9. Sci Rep. 2019. PMID: 30872729 Free PMC article. - A remarkable effect of the combination of probabilistic peer-punishment and coevolutionary mechanism on the evolution of cooperation.
Ohdaira T. Ohdaira T. Sci Rep. 2017 Sep 29;7(1):12448. doi: 10.1038/s41598-017-12742-4. Sci Rep. 2017. PMID: 28963526 Free PMC article. - Egoistic punishment outcompetes altruistic punishment in the spatial public goods game.
Li J, Liu Y, Wang Z, Xia H. Li J, et al. Sci Rep. 2021 Mar 22;11(1):6584. doi: 10.1038/s41598-021-85814-1. Sci Rep. 2021. PMID: 33753774 Free PMC article.
References
- Herrmann B., Thöni C. & Gächter S. Antisocial punishment across societies. Science 319, 1362–1367 (2008). - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources