Fully Mechanically Controlled Automated Electron Microscopic Tomography - PubMed (original) (raw)
Hongchang Li 1 3, Lei Zhang 1, Matthew Rames 1, Meng Zhang 1, Yadong Yu 1, Bo Peng 1, César Díaz Celis 4, April Xu 5, Qin Zou 6, Xu Yang 3, Xuefeng Chen 2, Gang Ren 1
Affiliations
- PMID: 27403922
- PMCID: PMC4941525
- DOI: 10.1038/srep29231
Fully Mechanically Controlled Automated Electron Microscopic Tomography
Jinxin Liu et al. Sci Rep. 2016.
Abstract
Knowledge of three-dimensional (3D) structures of each individual particles of asymmetric and flexible proteins is essential in understanding those proteins' functions; but their structures are difficult to determine. Electron tomography (ET) provides a tool for imaging a single and unique biological object from a series of tilted angles, but it is challenging to image a single protein for three-dimensional (3D) reconstruction due to the imperfect mechanical control capability of the specimen goniometer under both a medium to high magnification (approximately 50,000-160,000×) and an optimized beam coherence condition. Here, we report a fully mechanical control method for automating ET data acquisition without using beam tilt/shift processes. This method could reduce the accumulation of beam tilt/shift that used to compensate the error from the mechanical control, but downgraded the beam coherence. Our method was developed by minimizing the error of the target object center during the tilting process through a closed-loop proportional-integral (PI) control algorithm. The validations by both negative staining (NS) and cryo-electron microscopy (cryo-EM) suggest that this method has a comparable capability to other ET methods in tracking target proteins while maintaining optimized beam coherence conditions for imaging.
Conflict of interest statement
Q.Z. and A.X. are current employees for Pfizer Inc.
Figures
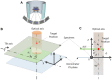
Figure 1. Schematics of the relationship between the optic axis and tilt axis within the TEM.
(A) A cartoon view of tomography, through a tilted sample stage. (B) 3D schematic view of the relationship between the optical axis and tilt axis within the TEM goniometer, specimen and imaging target diagram, where d z and d y determine the displacement from the tilt axis to the target position. (C) Side view of B, where θ = φ is the zero-tilt angle of the target position relative to the tilt axis.
Figure 2. Three major sources of mechanical errors and backlash correction.
(A) Motion control error from repeated X and Y motions with steps of 400 and 10 nm. (B) Backlash error from X and Y motion, caused by uneven gear meshing within the stage driver. (C) Trajectory error: unrepeatable tilt trajectory of X and Y resulting from non-ideal mechanical alignment. (D) Motion control error after backlash correction. Residual backlash error plot of X and Y motion after backlash elimination.
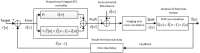
Figure 3. Overview of the Proportional-Integral (PI) control system.
Overview of the PI control system. Initially, the PI controller uses the previous errors to calculate the push  [_n_] for the next goniometer motion to correct the previous positional error. Goniometer motion incurs additional environmental error
[_n_] for the next goniometer motion to correct the previous positional error. Goniometer motion incurs additional environmental error  [_n_], which yields the shift
[_n_], which yields the shift  [_n_] through imaging and cross-correlation. The accumulated shift
[_n_] through imaging and cross-correlation. The accumulated shift  [_n_] is calculated by incorporating the historical motion
[_n_] is calculated by incorporating the historical motion  [n − _1_] and the current shift
[n − _1_] and the current shift  [_n_]. This
[_n_]. This  [_n_] is used as historical data for the next tilt loop. The difference of
[_n_] is used as historical data for the next tilt loop. The difference of  [_n_] from the target
[_n_] from the target  [_n_] is the residual error
[_n_] is the residual error  [n]. Within the proportional integral (PI) controller, the accumulated residual error
[n]. Within the proportional integral (PI) controller, the accumulated residual error  [_n_] is calculated by incorporating the historical error
[_n_] is calculated by incorporating the historical error  [n − _1_] and current residual error
[n − _1_] and current residual error  [n].
[n].
Figure 4. The procedure for measuring the XY shift of tilted images.
(A) the (n − 1)th tilted image is first stretched along the perpendicular direction to the tilting axis to compensate the effect of the tilt angle difference from the n th image, and then padded into an area twice as large before Fourier transfer. (B) The n th tilted image was directly padded into an area twice as large for Fourier transfer. (C) Based on inputted cut-off frequencies for band-pass filtering, a mask in reciprocal space was generated and applied to calculate the modified cross-correlation. (D) The revised Fourier transfer of the modified cross-correlation showed a peak to represent the defined XY shift.
Figure 5. The procedure for defining the defocus of a tilted image.
(A) The whole micrograph is divided into 8 × 8 mosaic tiles. (B) Each sub-image was used to measure the defocus after Fourier transfer. (C) Though a modified power spectrum (PS) of the sub-image, (D) the curve was compared with the theoretical contrast transfer function (CTF) curve via the calculation of the cross-correlation within a defined frequency range. (E) By screening the defocus within a searching range, the defocus which maximized the cross-correlation (CC) between the modified experimental curve and theoretical curve was used as the measured defocus for this sub-image. (F) By repeating the above procedure on each of the other sub-images, we obtained the defocus distribution against their whole micrograph. (G) The distribution can be fitted with a linear gradient distribution plane. (H) By subtracting this plane from the original 2D distribution, we could obtain a distribution of the residuals for defining the “bad” defocus measurements within the sub-images. The bad measured defocus was defined as any residual above twice the standard deviation (such as the two defocuses marked in red crosses). After the bad defocus tiles are removed, the defocus distribution was then re-fitted a linear distribution plane, and the defocus at the center was used as the defocus of the tilted micrograph.
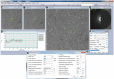
Figure 6. Graphical user interface of the tomography software.
(A) Imaging area of the current, (B,C) previous and next previous collected images. (D) Plot of the positional and defocus errors during tomography collection. (E) Fast-Fourier transformation (FFT) of the current image and fitted contrast transfer function (CTF) curve. (F) Control panel for tomographic parameters, options, and process status. (G) Control panel for position tracking, defocus tracking and fitting.
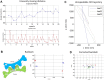
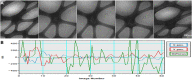
Figure 7. Automatic tomography data collection of negative-stained nucleosome-DNA complex and antibody conjugate.
(A) A negatively stained nucleosome-DNA sample collected from −60° to +60° with a 1.5° step under 160,000× magnification and an expected defocus of 400 nm. (B) This series took 1.5 h to collect, with X/Y mean absolute positional errors and a defocus error of 17.8, 17.6, and 21.6 nm, respectively, with standard deviations of 24.6, 21.1 and 26.9 nm, respectively. (C) A negatively stained antibody conjugate sample collected from −60° to +60° with a 1.5° step under 80,000× magnification and an expected defocus of 800 nm. (D) This series took 1.5 h to collect, with X/Y mean absolute positional errors and a defocus error of 13.1, 17.1, and 22.9 nm, respectively, with standard deviations of 18.3, 20.7 and 29.1 nm, respectively.
Figure 8. Automatic tomography data collection of low-density lipoprotein.
(A) A Cryo-EM LDL sample collected from −60° to +58° with a 2° step under 50,000× magnification and an expected defocus of 2,000 nm. (B) This series took 1 h and 15 min to collect, with X/Y mean absolute positional errors and a defocus error of 43.0 nm 78.4, and 221.8 nm, respectively, with standard deviations of 61.1, 108.6 and 340.2 nm, respectively.
Similar articles
- LoTToR: An Algorithm for Missing-Wedge Correction of the Low-Tilt Tomographic 3D Reconstruction of a Single-Molecule Structure.
Zhai X, Lei D, Zhang M, Liu J, Wu H, Yu Y, Zhang L, Ren G. Zhai X, et al. Sci Rep. 2020 Jun 26;10(1):10489. doi: 10.1038/s41598-020-66793-1. Sci Rep. 2020. PMID: 32591588 Free PMC article. - An Algorithm for Enhancing the Image Contrast of Electron Tomography.
Wu H, Zhai X, Lei D, Liu J, Yu Y, Bie R, Ren G. Wu H, et al. Sci Rep. 2018 Nov 12;8(1):16711. doi: 10.1038/s41598-018-34652-9. Sci Rep. 2018. PMID: 30420636 Free PMC article. - IPET and FETR: experimental approach for studying molecular structure dynamics by cryo-electron tomography of a single-molecule structure.
Zhang L, Ren G. Zhang L, et al. PLoS One. 2012;7(1):e30249. doi: 10.1371/journal.pone.0030249. Epub 2012 Jan 24. PLoS One. 2012. PMID: 22291925 Free PMC article. - Electron tomography in plant cell biology.
Otegui MS, Pennington JG. Otegui MS, et al. Microscopy (Oxf). 2019 Feb 1;68(1):69-79. doi: 10.1093/jmicro/dfy133. Microscopy (Oxf). 2019. PMID: 30452668 Review. - Cryo-electron tomography in biology and medicine.
Koning RI, Koster AJ. Koning RI, et al. Ann Anat. 2009 Nov;191(5):427-45. doi: 10.1016/j.aanat.2009.04.003. Epub 2009 Jun 9. Ann Anat. 2009. PMID: 19559584 Review.
Cited by
- IgG Antibody 3D Structures and Dynamics.
Jay JW, Bray B, Qi Y, Igbinigie E, Wu H, Li J, Ren G. Jay JW, et al. Antibodies (Basel). 2018 Apr 19;7(2):18. doi: 10.3390/antib7020018. Antibodies (Basel). 2018. PMID: 31544870 Free PMC article. Review. - Designer molecules of the synaptic organizer MDGA1 reveal 3D conformational control of biological function.
Lee H, Chofflet N, Liu J, Fan S, Lu Z, Resua Rojas M, Penndorf P, Bailey AO, Russell WK, Machius M, Ren G, Takahashi H, Rudenko G. Lee H, et al. J Biol Chem. 2023 Apr;299(4):104586. doi: 10.1016/j.jbc.2023.104586. Epub 2023 Mar 7. J Biol Chem. 2023. PMID: 36889589 Free PMC article. - Three-dimensional structural dynamics of DNA origami Bennett linkages using individual-particle electron tomography.
Lei D, Marras AE, Liu J, Huang CM, Zhou L, Castro CE, Su HJ, Ren G. Lei D, et al. Nat Commun. 2018 Feb 9;9(1):592. doi: 10.1038/s41467-018-03018-0. Nat Commun. 2018. PMID: 29426880 Free PMC article. - Facile hermetic TEM grid preparation for molecular imaging of hydrated biological samples at room temperature.
Kong L, Liu J, Zhang M, Lu Z, Xue H, Ren A, Liu J, Li J, Ling WL, Ren G. Kong L, et al. Nat Commun. 2023 Sep 13;14(1):5641. doi: 10.1038/s41467-023-41266-x. Nat Commun. 2023. PMID: 37704637 Free PMC article. - Facile hermetic TEM grid preparation for molecular imaging of hydrated biological samples at room temperature.
Kong L, Liu J, Zhang M, Lu Z, Xue H, Ren A, Liu J, Li J, Li Ling W, Ren G. Kong L, et al. Res Sq [Preprint]. 2023 Feb 14:rs.3.rs-2464569. doi: 10.21203/rs.3.rs-2464569/v1. Res Sq. 2023. PMID: 36824820 Free PMC article. Updated. Preprint.
References
- Urban E., Jacob S., Nemethova M., Resch G. P. & Small J. V. Electron tomography reveals unbranched networks of actin filaments in lamellipodia. Nat Cell Biol 12, 429–435 (2010). - PubMed
- Medalia O. et al.. Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science 298, 1209–1213 (2002). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous