Inferring interaction partners from protein sequences - PubMed (original) (raw)
Inferring interaction partners from protein sequences
Anne-Florence Bitbol et al. Proc Natl Acad Sci U S A. 2016.
Abstract
Specific protein-protein interactions are crucial in the cell, both to ensure the formation and stability of multiprotein complexes and to enable signal transduction in various pathways. Functional interactions between proteins result in coevolution between the interaction partners, causing their sequences to be correlated. Here we exploit these correlations to accurately identify, from sequence data alone, which proteins are specific interaction partners. Our general approach, which employs a pairwise maximum entropy model to infer couplings between residues, has been successfully used to predict the 3D structures of proteins from sequences. Thus inspired, we introduce an iterative algorithm to predict specific interaction partners from two protein families whose members are known to interact. We first assess the algorithm's performance on histidine kinases and response regulators from bacterial two-component signaling systems. We obtain a striking 0.93 true positive fraction on our complete dataset without any a priori knowledge of interaction partners, and we uncover the origin of this success. We then apply the algorithm to proteins from ATP-binding cassette (ABC) transporter complexes, and obtain accurate predictions in these systems as well. Finally, we present two metrics that accurately distinguish interacting protein families from noninteracting ones, using only sequence data.
Keywords: coevolution; direct coupling analysis; maximum entropy; paralogs; protein−protein interactions.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
Fig. 1.
Iterative pairing algorithm (IPA). (A) Surface representations of an HK dimer (top) and an RR (bottom), from a cocrystal structure (27); the HK−RR contacts in each molecule are highlighted in color. (B) To correctly pair HKs and RRs in each species from their sequences alone, we start from multiple sequence alignments of HKs and RRs, including 64 amino acids from the HK and 112 from the RR. (C) Schematic of the main steps of the IPA. (D and E) Example of HK−RR pair assignment and ranking by energy gap for one species. (D) Color map of the matrix of HK−RR interaction energies in E. coli K-12 MG1655 from the final iteration of the IPA performed on our standard dataset, with a training set of Nstart=100 HK−RR pairs, and an increment step of Nincrement=200 pairs. As in every IPA iteration and every species, the pair with the lowest interaction energy is selected first (here, HK 10 and RR 10, boxed in white), and this HK and RR are removed from further consideration (black hatches). Then, the next pair with the lowest energy is chosen, and the process is repeated until all HKs and RRs are paired. (E) Energy spectrum from D, showing the interaction energies with all of the HKs for each RR, with the correct HK−RR pairs shown in red. The energy gap ΔE is shown for RR 10. A confidence score based on the energy gap is used to rank all assigned HK−RR pairs, and this ranking is exploited to build the CA for the subsequent IPA iteration. See Materials and Methods for details.
Fig. 2.
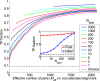
Fraction of predicted pairs that are true positives (TP fraction), for different training set sizes Nstart. The progression of the TP fraction during iterations of the IPA is shown. The TP fraction is plotted versus the effective number of HK-RR pairs (Meff; see SI Appendix, Eq. S1) in the CA, which includes Nincrement=6 additional pairs at each iteration. The IPA is performed on the standard dataset, and all results are averaged over 50 replicates that differ by the random choice of training pairs. The dashed line shows the average TP fraction obtained for random HK−RR pairings. (Inset) Initial and final TP fractions (at first and last iteration) versus Nstart.
Fig. 3.
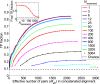
Starting from random pairings, i.e., without known pairings. Shown is the TP fraction during iterations of the IPA versus the effective number of HK−RR pairs (Meff) in the CA, which includes Nincrement additional pairs at each iteration. Different curves correspond to different Nincrement. The IPA is performed on the standard dataset, and all results are averaged over 50 replicates that differ in their initial random pairings. Note that the first point of each curve corresponds to the second iteration. The dashed line shows the average TP fraction obtained for random HK−RR pairings. (Inset) Final TP fraction versus Nincrement.
Fig. 4.
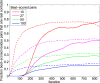
Training of the couplings during the IPA. Residue pairs comprising an HK site and an RR site were scored by the Frobenius norm (i.e., the square root of the summed squares) of the couplings involving all possible residue types at these two sites. The best-scored residue pairs were compared with the 27 HK−RR contacts found experimentally in ref. . Solid curves show the fraction of residue pairs that are real contacts (among the k best-scored pairs for four different values of k) versus the iteration number in the IPA. Dashed curves represent the ideal case, where, at each iteration, Nincrement randomly selected correct HK−RR pairs are added to the CA. The overall fraction of residue pairs that are real HK−RR contacts, yielding the chance expectation, is only 3.8×10−3. The IPA is performed on the standard dataset with Nincrement=6, and all data are averaged over 500 replicates that differ in their initial random pairings.
Fig. 5.
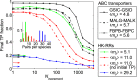
Results for ABC transporter pairs and impact of the number of pairs per species. Shown is the final TP fraction versus Nincrement for three different pairs of protein families involved in ABC transport complexes (black curves), and for three HK−RR datasets with different distributions of the number of pairs per species yielding different means 〈mp〉 (colored curves). All datasets include ∼5,000 protein pairs, and the IPA is started from random pairings, apart from the red dashed curve, where it is started from incorrect random pairings. All results are averaged over 50 replicates that differ in their initial pairings. Arrows with the same line style as each curve indicate the average TP fractions obtained for random pairings in each dataset. (Inset) Distribution of the number of pairs per species in the three different HK−RR datasets (red, standard dataset; green and blue, datasets comprising the species with, respectively, lowest or highest numbers of pairs in the full HK−RR dataset).
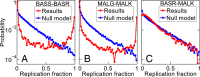
Fig. 6.
An IPA-derived signature of protein−protein interactions. For three pairs of protein families, we compute the fraction fr of IPA replicates in which each possible within-species protein pair is predicted as a pair. (A and B) Protein families with known interactions: (A) BASS−BASR homologs and (B) MALG−MALK homologs. (C) Protein families with no known interaction (BASR–MALK homologs). Red curves show the distribution of fr obtained for each alignment. Blue curves show the same distribution obtained by running the IPA on alignments where each column is scrambled (null model). Alignments include ∼5,000 pairs, with 〈mp〉≈5, and each distribution is estimated from 500 IPA replicates that differ in their initial random pairings, using Nincrement=50.
Similar articles
- Inferring interaction partners from protein sequences using mutual information.
Bitbol AF. Bitbol AF. PLoS Comput Biol. 2018 Nov 13;14(11):e1006401. doi: 10.1371/journal.pcbi.1006401. eCollection 2018 Nov. PLoS Comput Biol. 2018. PMID: 30422978 Free PMC article. - Phylogenetic correlations can suffice to infer protein partners from sequences.
Marmier G, Weigt M, Bitbol AF. Marmier G, et al. PLoS Comput Biol. 2019 Oct 14;15(10):e1007179. doi: 10.1371/journal.pcbi.1007179. eCollection 2019 Oct. PLoS Comput Biol. 2019. PMID: 31609984 Free PMC article. - Simultaneous identification of specifically interacting paralogs and interprotein contacts by direct coupling analysis.
Gueudré T, Baldassi C, Zamparo M, Weigt M, Pagnani A. Gueudré T, et al. Proc Natl Acad Sci U S A. 2016 Oct 25;113(43):12186-12191. doi: 10.1073/pnas.1607570113. Epub 2016 Oct 11. Proc Natl Acad Sci U S A. 2016. PMID: 27729520 Free PMC article. - The Type 1 secretion pathway - the hemolysin system and beyond.
Thomas S, Holland IB, Schmitt L. Thomas S, et al. Biochim Biophys Acta. 2014 Aug;1843(8):1629-41. doi: 10.1016/j.bbamcr.2013.09.017. Epub 2013 Oct 12. Biochim Biophys Acta. 2014. PMID: 24129268 Review. - Structure and mechanism of energy-coupling factor transporters.
Zhang P. Zhang P. Trends Microbiol. 2013 Dec;21(12):652-9. doi: 10.1016/j.tim.2013.09.009. Epub 2013 Oct 21. Trends Microbiol. 2013. PMID: 24156876 Review.
Cited by
- Toward Characterising the Cellular 3D-Proteome.
Elofsson A. Elofsson A. Front Bioinform. 2021 Mar 29;1:598878. doi: 10.3389/fbinf.2021.598878. eCollection 2021. Front Bioinform. 2021. PMID: 36353353 Free PMC article. No abstract available. - Predicting Protein-Protein Interaction Sites Using Sequence Descriptors and Site Propensity of Neighboring Amino Acids.
Kuo TH, Li KB. Kuo TH, et al. Int J Mol Sci. 2016 Oct 26;17(11):1788. doi: 10.3390/ijms17111788. Int J Mol Sci. 2016. PMID: 27792167 Free PMC article. - Inferring interaction partners from protein sequences using mutual information.
Bitbol AF. Bitbol AF. PLoS Comput Biol. 2018 Nov 13;14(11):e1006401. doi: 10.1371/journal.pcbi.1006401. eCollection 2018 Nov. PLoS Comput Biol. 2018. PMID: 30422978 Free PMC article. - Power law tails in phylogenetic systems.
Qin C, Colwell LJ. Qin C, et al. Proc Natl Acad Sci U S A. 2018 Jan 23;115(4):690-695. doi: 10.1073/pnas.1711913115. Epub 2018 Jan 8. Proc Natl Acad Sci U S A. 2018. PMID: 29311320 Free PMC article. - New Techniques for Ancient Proteins: Direct Coupling Analysis Applied on Proteins Involved in Iron Sulfur Cluster Biogenesis.
Fantini M, Malinverni D, De Los Rios P, Pastore A. Fantini M, et al. Front Mol Biosci. 2017 Jun 15;4:40. doi: 10.3389/fmolb.2017.00040. eCollection 2017. Front Mol Biosci. 2017. PMID: 28664160 Free PMC article.
References
- Altschuh D, Lesk AM, Bloomer AC, Klug A. Correlation of co-ordinated amino acid substitutions with function in viruses related to tobacco mosaic virus. J Mol Biol. 1987;193(4):693–707. - PubMed
- Lockless SW, Ranganathan R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science. 1999;286(5438):295–299. - PubMed
- Lapedes AS, Giraud BG, Liu L, Stormo GD. 1999. Correlated mutations in models of protein sequences: Phylogenetic and structural effects. Statistics in Molecular Biology and Genetics, Lecture Notes Monograph Series, ed Seillier-Moiseiwitsch F (Am Math Soc, Providence, RI), Vol 33, pp 236–256.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources