Removal of batch effects using distribution-matching residual networks - PubMed (original) (raw)

Removal of batch effects using distribution-matching residual networks

Uri Shaham et al. Bioinformatics. 2017.

Abstract

Motivation: Sources of variability in experimentally derived data include measurement error in addition to the physical phenomena of interest. This measurement error is a combination of systematic components, originating from the measuring instrument and random measurement errors. Several novel biological technologies, such as mass cytometry and single-cell RNA-seq (scRNA-seq), are plagued with systematic errors that may severely affect statistical analysis if the data are not properly calibrated.

Results: We propose a novel deep learning approach for removing systematic batch effects. Our method is based on a residual neural network, trained to minimize the Maximum Mean Discrepancy between the multivariate distributions of two replicates, measured in different batches. We apply our method to mass cytometry and scRNA-seq datasets, and demonstrate that it effectively attenuates batch effects.

Availability and implementation: our codes and data are publicly available at https://github.com/ushaham/BatchEffectRemoval.git.

Contact: yuval.kluger@yale.edu.

Supplementary information: Supplementary data are available at Bioinformatics online.

© The Author (2017). Published by Oxford University Press. All rights reserved. For Permissions, please email: journals.permissions@oup.com

PubMed Disclaimer

Figures

Fig. 1

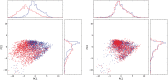
Fig. 1

Calibration of CyTOF data. Projection of the source (red) and target (blue) samples on the first two principal components of the target data. Left: before calibration. Right: after calibration

Fig. 2

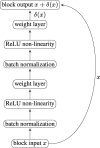
Fig. 2

A typical ResNet block

Fig. 3

Fig. 3

Quality of calibration in terms of the marginal distribution of each marker. Empirical cumulative distribution functions of the first three markers in the CyTOF calibration experiment. In each plot the full, dashed and dotted curves corresponds to the target, source and calibrated source samples, respectively. In each marker the full and dotted curves are substantially closer than the full and dashed curves

Fig. 4

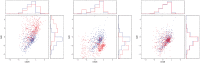
Fig. 4

Calibration of CyTOF data: CD8 + T-cells cells (red) and target (blue) samples in the (CD28, GzB) plane. Left: before calibration. Center: calibration using MLP. Right, calibration using ResNet

Fig. 5

Fig. 5

Histograms of the 25 _P_-values of Kolmogorov-Smirnov tests, comparing the distributions of the calibrated data with the target distribution of each of the 25 markers

Fig. 6

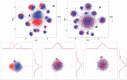
Fig. 6

Calibration of scRNA-seq. Top: _t_-SNE plots before (left) and after (right) calibration using MMD-ResNet. Bottom: Calibration of cells with high expression of Prkca. _t_-SNE plots before calibration (left), after calibration using Combat (middle) and MMD-ResNet (right)

Similar articles

Cited by

References

    1. Dziugaite G.K. et al. (2015). Training generative neural networks via maximum mean discrepancy optimization. Uncertainty in Artificial Intelligence-Proceedings of the 31st Conference. UAI 2015, 258–267.
    1. Finck R. et al. (2013) Normalization of mass cytometry data with bead standards. Cytometry Part A, 83, 483–494. - PMC - PubMed
    1. Glorot X., Bengio Y. (2010) Understanding the difficulty of training deep feedforward neural networks. In Proceedings of AISTATS, Sardinia, Italy, vol 9, pp. 249–256.
    1. Gretton A. et al. (2006) A kernel method for the two-sample-problem. Advances in Neural Information Processing Systems, 19, 513–520.
    1. Gretton A. et al. (2012) A kernel two-sample test. J. Mach. Learn. Res., 13, 723–773.

MeSH terms

LinkOut - more resources