The steady aerodynamics of aerofoils with porosity gradients - PubMed (original) (raw)
The steady aerodynamics of aerofoils with porosity gradients
Rozhin Hajian et al. Proc Math Phys Eng Sci. 2017 Sep.
Abstract
This theoretical study determines the aerodynamic loads on an aerofoil with a prescribed porosity distribution in a steady incompressible flow. A Darcy porosity condition on the aerofoil surface furnishes a Fredholm integral equation for the pressure distribution, which is solved exactly and generally as a Riemann-Hilbert problem provided that the porosity distribution is Hölder-continuous. The Hölder condition includes as a subset any continuously differentiable porosity distributions that may be of practical interest. This formal restriction on the analysis is examined by a class of differentiable porosity distributions that approach a piecewise, discontinuous function in a certain parametric limit. The Hölder-continuous solution is verified in this limit against analytical results for partially porous aerofoils in the literature. Finally, a comparison made between the new theoretical predictions and experimental measurements of SD7003 aerofoils presented in the literature. Results from this analysis may be integrated into a theoretical framework to optimize turbulence noise suppression with minimal impact to aerodynamic performance.
Keywords: Riemann–Hilbert problem; silent owl flight; trailing-edge noise.
Conflict of interest statement
We declare we have no competing interests.
Figures
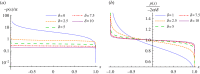
Figure 1.
Normalized pressure distribution of a uniformly porous flat aerofoil for different porosity parameters δ: (a) pressure jump normalized by angle of attack, −p(x)/α; (b) pressure jump normalized by the high porosity limit, −p(x)/(2_α_/δ). (Online version in colour.)
Figure 2.
Porosity and pressure distributions of a thin aerofoil with a prescribed differentiable porosity distribution given by (4.8) with _a_=−0.5: (a) porosity distributions for _r_=10 and r→∞; (b) pressure distributions for _r_=10 and the singular limit as r→∞ for the flat aerofoil. The dashed line indicates Iosilevskii’s result, eqn (13) in [18]. (Online version in colour.)
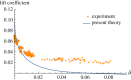
Figure 3.
Comparison of the predicted and measured lift coefficients of a porous SD7003 aerofoil at zero angle of attack for various porosity constants δ. (Online version in colour.)
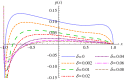
Figure 4.
Pressure distribution of a porous SD7003 aerofoil at zero angle of attack for various porosity constants δ, based on the theoretical model. (Online version in colour.)
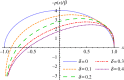
Figure 5.
Normalized pressure distribution, −p(x)/β, of a uniformly porous cambered aerofoil at zero angle of attack (_α_=0) for different porosity constants δ. (Online version in colour.)
Similar articles
- Potential flow through a cascade of aerofoils: direct and inverse problems.
Baddoo PJ, Ayton LJ. Baddoo PJ, et al. Proc Math Phys Eng Sci. 2018 Sep;474(2217):20180065. doi: 10.1098/rspa.2018.0065. Epub 2018 Sep 12. Proc Math Phys Eng Sci. 2018. PMID: 30333697 Free PMC article. - Bioinspired aerofoil adaptations: the next steps for theoretical models.
Ayton LJ. Ayton LJ. Philos Trans A Math Phys Eng Sci. 2019 Dec 2;377(2159):20190070. doi: 10.1098/rsta.2019.0070. Epub 2019 Oct 14. Philos Trans A Math Phys Eng Sci. 2019. PMID: 31607251 Free PMC article. - Effect of trailing-edge serrations on noise reduction in a coupled bionic aerofoil inspired by barn owls.
Li D, Liu X, Hu F, Wang L. Li D, et al. Bioinspir Biomim. 2019 Dec 4;15(1):016009. doi: 10.1088/1748-3190/ab529e. Bioinspir Biomim. 2019. PMID: 31665715 - The PELskin project-part V: towards the control of the flow around aerofoils at high angle of attack using a self-activated deployable flap.
Rosti ME, Kamps L, Bruecker C, Omidyeganeh M, Pinelli A. Rosti ME, et al. Meccanica. 2017;52(8):1811-1824. doi: 10.1007/s11012-016-0524-x. Epub 2016 Sep 27. Meccanica. 2017. PMID: 28529384 Free PMC article. - Unsteady aerodynamics of insect flight.
Ellington CP. Ellington CP. Symp Soc Exp Biol. 1995;49:109-29. Symp Soc Exp Biol. 1995. PMID: 8571220 Review.
Cited by
- Potential flow through a cascade of aerofoils: direct and inverse problems.
Baddoo PJ, Ayton LJ. Baddoo PJ, et al. Proc Math Phys Eng Sci. 2018 Sep;474(2217):20180065. doi: 10.1098/rspa.2018.0065. Epub 2018 Sep 12. Proc Math Phys Eng Sci. 2018. PMID: 30333697 Free PMC article.
References
- Brooks TF, Pope DS, Marcolini MA. 1989. Airfoil self-noise and prediction. NASA Technical Reports Server, vol. 1218.
- Hayden RE. 1976. Reduction of noise from airfoils and propulsive lift systems using variable impedance systems. In 3rd AIAA Aeroacoustics Conf., Palo Alto, CA, USA, Paper AIAA-1976-500. Reston, VA: AIAA.
- Ffowcs Williams JE, Hall LH. 1970. Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid. Mech. 40, 657–670. (doi:10.1017/S0022112070000368) - DOI
- Howe MS. 1993. Structural and acoustic noise produced by turbulent flow over an elastic trailing edge. Proc. R. Soc. Lond. A 442, 533–554. (doi:10.1098/rspa.1993.0120) - DOI
- Howe MS. 1998. Acoustics of fluid-structure interactions. Cambridge, UK: Cambridge University Press.
LinkOut - more resources
Full Text Sources
Other Literature Sources