The reproducibility of research and the misinterpretation of p-values - PubMed (original) (raw)
. 2017 Dec 6;4(12):171085.
doi: 10.1098/rsos.171085. eCollection 2017 Dec.
Affiliations
- PMID: 29308247
- PMCID: PMC5750014
- DOI: 10.1098/rsos.171085
The reproducibility of research and the misinterpretation of _p_-values
David Colquhoun. R Soc Open Sci. 2017.
Erratum in
- Correction to 'The reproducibility of research and the misinterpretation of _p_-values'.
Colquhoun D. Colquhoun D. R Soc Open Sci. 2018 Mar 7;5(3):180100. doi: 10.1098/rsos.180100. eCollection 2018 Mar. R Soc Open Sci. 2018. PMID: 29658963 Free PMC article.
Abstract
We wish to answer this question: If you observe a 'significant' _p_-value after doing a single unbiased experiment, what is the probability that your result is a false positive? The weak evidence provided by _p-_values between 0.01 and 0.05 is explored by exact calculations of false positive risks. When you observe p = 0.05, the odds in favour of there being a real effect (given by the likelihood ratio) are about 3 : 1. This is far weaker evidence than the odds of 19 to 1 that might, wrongly, be inferred from the _p-_value. And if you want to limit the false positive risk to 5%, you would have to assume that you were 87% sure that there was a real effect before the experiment was done. If you observe p = 0.001 in a well-powered experiment, it gives a likelihood ratio of almost 100 : 1 odds on there being a real effect. That would usually be regarded as conclusive. But the false positive risk would still be 8% if the prior probability of a real effect were only 0.1. And, in this case, if you wanted to achieve a false positive risk of 5% you would need to observe p = 0.00045. It is recommended that the terms 'significant' and 'non-significant' should never be used. Rather, _p-_values should be supplemented by specifying the prior probability that would be needed to produce a specified (e.g. 5%) false positive risk. It may also be helpful to specify the minimum false positive risk associated with the observed _p-_value. Despite decades of warnings, many areas of science still insist on labelling a result of p < 0.05 as 'statistically significant'. This practice must contribute to the lack of reproducibility in some areas of science. This is before you get to the many other well-known problems, like multiple comparisons, lack of randomization and _p-_hacking. Precise inductive inference is impossible and replication is the only way to be sure. Science is endangered by statistical misunderstanding, and by senior people who impose perverse incentives on scientists.
Keywords: false positive risk; null hypothesis tests; reproducibility; significance tests; statistics.
Conflict of interest statement
I declare I have no competing interests.
Figures
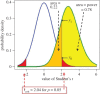
Figure 1.
Definitions for a NHST. A Student's _t-_test is used to analyse the difference between the means of two groups of n = 16 observations. The t value, therefore, has 2(n − 1) = 30 d.f. The blue line represents the distribution of Student's t under the null hypothesis (_H_0): the true difference between means is zero. The green line shows the non-central distribution of Student's t under the alternative hypothesis (_H_1): the true difference between means is 1 (1 s.d.). The critical value of t for 30 d.f. and p = 0.05 is 2.04, so, for a two-sided test, any value of t above 2.04, or below –2.04, would be deemed ‘significant’. These values are represented by the red areas. When the alternative hypothesis is true (green line), the probability that the value of t is below the critical level (2.04) is 22% (gold shaded): these represent false negative results. Consequently, the area under the green curve above t = 2.04 (shaded yellow) is the probability that a ‘significant’ result will be found when there is in fact a real effect (_H_1 is true): this is the power of the test, in this case 78%. The ordinates marked _y_0 (= 0.526) and _y_1 (= 0.290) are used to calculate likelihood ratios, as in §5.
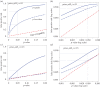
Figure 2.
Plots of false positive risk (FPR) against _p_-value, for two different ways of calculating FPR. The continuous blue line shows the p-equals interpretation and the dashed blue line shows the p-less-than interpretation. These curves are calculated for a well-powered experiment with a sample size of n = 16. This gives power = 0.78, for p = 0.05 in our example (true effect = 1 s.d.). (a,b) Prior probability of a real effect = 0.1. (c,d) Prior probability of a real effect = 0.5. The dashed red line shows a unit slope: this shows the relationship that would hold if the FPR were the same as the _p_-value. The graphs in the right-hand column are the same as those in the left-hand column, but in the form of a log–log plot. Graphs produced by _Plot-FPR-versus_-Pval.R (see the electronic supplementary material).
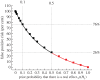
Figure 3.
The false positive risk plotted against the prior probability for a test that comes out with a _p_-value just below 0.05. The points for prior probabilities greater than 0.5 are red because it is essentially never legitimate to assume a prior bigger than 0.5. The calculations are done with a sample size of 16, giving power = 0.78 for p = 0.0475. The square symbols were found by simulation of 100 000 tests and looking only at tests that give _p_-values between 0.045 and 0.05. The fraction of these tests for which the null hypothesis is true is the false positive risk. The continuous line is the theoretical calculation of the same thing: the numbers were calculated with origin-graph.R and transferred to origin to make the plot.
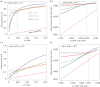
Figure 4.
The calculated false positive risk plotted against the observed _p_-value. The plots are for three different sample sizes: n = 4 (red), n = 8 (green) and n = 16 (blue). (a,b) Prior probability of a real effect = 0.1. (c,d) Prior probability of a real effect = 0.5. The dashed red line shows a unit slope: this shows the relationship that would hold if the FPR were the same as the _p_-value. The graphs in the right-hand column are the same as those in the left-hand column, but in the form of a log–log plot. Graphs produced by _Plot-FPR-versus_-Pval.R (see the electronic supplementary material).
Figure 5.
Web calculator [12] for the case where we observe a _p_-value of 0.001 and the prior probability of a real effect is 0.1 (
).
Figure 6.
Web calculator [12] calculation of the prior probability that would be needed to achieve a false positive risk of 5% when we observe p = 0.05 (
).
Similar articles
- An investigation of the false discovery rate and the misinterpretation of p-values.
Colquhoun D. Colquhoun D. R Soc Open Sci. 2014 Nov 19;1(3):140216. doi: 10.1098/rsos.140216. eCollection 2014 Nov. R Soc Open Sci. 2014. PMID: 26064558 Free PMC article. Review. - Review of null hypothesis significance testing in the ophthalmic literature: are most 'significant' P values false positives?
Sanfilippo PG, Casson RJ, Yazar S, Mackey DA, Hewitt AW. Sanfilippo PG, et al. Clin Exp Ophthalmol. 2016 Jan-Feb;44(1):52-61. doi: 10.1111/ceo.12570. Epub 2015 Jul 27. Clin Exp Ophthalmol. 2016. PMID: 26140666 Review. - Why and how we should join the shift from significance testing to estimation.
Berner D, Amrhein V. Berner D, et al. J Evol Biol. 2022 Jun;35(6):777-787. doi: 10.1111/jeb.14009. Epub 2022 May 18. J Evol Biol. 2022. PMID: 35582935 Free PMC article. - The reign of the p-value is over: what alternative analyses could we employ to fill the power vacuum?
Halsey LG. Halsey LG. Biol Lett. 2019 May 31;15(5):20190174. doi: 10.1098/rsbl.2019.0174. Biol Lett. 2019. PMID: 31113309 Free PMC article. - Bad statistical practice in pharmacology (and other basic biomedical disciplines): you probably don't know P.
Lew MJ. Lew MJ. Br J Pharmacol. 2012 Jul;166(5):1559-67. doi: 10.1111/j.1476-5381.2012.01931.x. Br J Pharmacol. 2012. PMID: 22394284 Free PMC article.
Cited by
- The Statistical Fragility of Platelet-Rich Plasma as Treatment for Plantar Fasciitis: A Systematic Review and Simulated Fragility Analysis.
Gupta A, Ortiz-Babilonia C, Xu AL, Rogers D, Vulcano E, Aiyer AA. Gupta A, et al. Foot Ankle Orthop. 2022 Dec 24;7(4):24730114221144049. doi: 10.1177/24730114221144049. eCollection 2022 Oct. Foot Ankle Orthop. 2022. PMID: 36582654 Free PMC article. - A response to critiques of 'The reproducibility of research and the misinterpretation of _p_-values'.
Colquhoun D. Colquhoun D. R Soc Open Sci. 2019 Nov 6;6(11):190819. doi: 10.1098/rsos.190819. eCollection 2019 Nov. R Soc Open Sci. 2019. PMID: 31827832 Free PMC article. No abstract available. - Reverse-Bayes methods for evidence assessment and research synthesis.
Held L, Matthews R, Ott M, Pawel S. Held L, et al. Res Synth Methods. 2022 May;13(3):295-314. doi: 10.1002/jrsm.1538. Epub 2021 Dec 30. Res Synth Methods. 2022. PMID: 34889058 Free PMC article. Review. - Giving science the finger-is the second-to-fourth digit ratio (2D:4D) a biomarker of good luck? A cross sectional study.
Smoliga JM, Fogaca LK, Siplon JS, Goldburt AA, Jakobs F. Smoliga JM, et al. BMJ. 2021 Dec 15;375:e067849. doi: 10.1136/bmj-2021-067849. BMJ. 2021. PMID: 34911738 Free PMC article. - Near-infrared hyperspectral imaging and robust statistics for in vivo non-melanoma skin cancer and actinic keratosis characterisation.
Courtenay LA, Barbero-García I, Martínez-Lastras S, Del Pozo S, Corral de la Calle M, Garrido A, Guerrero-Sevilla D, Hernandez-Lopez D, González-Aguilera D. Courtenay LA, et al. PLoS One. 2024 Apr 25;19(4):e0300400. doi: 10.1371/journal.pone.0300400. eCollection 2024. PLoS One. 2024. PMID: 38662718 Free PMC article.
References
- Bakan D. 1966. The test of significance in psychological research. Psychol. Bull. 66, 423–437. (doi:10.1037/h0020412) - DOI - PubMed
- Colquhoun D. 2014. An investigation of the false discovery rate and the misinterpretation of p-values. R. Soc. open sci. 1, 140216 (doi:10.1098/rsos.140216) - DOI - PMC - PubMed
- Berger JO, Sellke T. 1987. Testing a point null hypothesis—the irreconcilability of p-values and evidence. J. Am. Stat. Assoc. 82, 112–122. (doi:10.2307/2289131) - DOI
- Berger JO, Delampady M. 1987. Testing precise hypotheses. Stat. Sci. 2, 317–352. (doi:10.1214/ss/1177013238) - DOI
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafo MR. 2013. Power failure: why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 14, 365–376. (doi: 10.1038/nrn3475) - DOI - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources