Ewald sphere correction using a single side-band image processing algorithm - PubMed (original) (raw)
Ewald sphere correction using a single side-band image processing algorithm
Christopher J Russo et al. Ultramicroscopy. 2018 Apr.
Abstract
Curvature of the Ewald sphere limits the resolution at which Fourier components in an image can be approximated as corresponding to a projection of the object. Since the radius of the Ewald sphere is inversely proportional to the wavelength of the imaging electrons, this normally imposes a limit on the thickness of specimen for which images can be easily interpreted to a particular resolution. Here we present a computational method for precisely correcting for the curvature of the Ewald sphere using defocused images that delocalise the high-resolution Fourier components from the primary image. By correcting for each approximately Friedel-symmetry-related sideband separately using two distinct complex transforms that effectively move the displaced Fourier components back to where they belong in the structure, we can determine the amplitude and phase of each of the Fourier components separately. This precisely accounts for the effect of Ewald sphere curvature over a bandwidth defined by the defocus and the size of the particle being imaged. We demonstrate this processing algorithm using: 1. simulated images of a particle with only a single, high-resolution Fourier component, and 2. experimental images of gold nanoparticles embedded in ice. Processing micrographs with this algorithm will allow higher resolution imaging of thicker specimens at lower energies without any image degradation or blurring due to errors made by the assumption of a flat Ewald sphere. Although the procedure will work best on images recorded with higher defocus settings than used normally, it should still improve 3D single-particle structure determination using images recorded at any defocus and any electron energy. Finally, since the Ewald sphere curvature is in a known direction in the third dimension which is parallel to the direction of view, this algorithm automatically determines the absolute hand of the specimen without the need for pairs of images with a known tilt angle difference.
Keywords: CTF; Depth of field; Ewald sphere; Single-particle reconstruction; Structure determination; cryoEM.
Copyright © 2018 MRC Laboratory of Molecular Biology. Published by Elsevier B.V. All rights reserved.
Figures
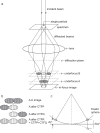
Fig. 1
(a) Diagram showing how underfocused images keep two approximately Friedel-related diffraction patterns completely separate so that they do not overlap in the image. Since they do not overlap physically in the image, their amplitude and phase can be recovered by an appropriate image processing procedure. At underfocus B, the two diffracted beams are fully resolved from the low-resolution shadow of the particle, whereas underfocus A is the minimum underfocus needed to avoid any overlap of the high-resolution information. (b) The result of applying the two CTFP and CTFQ procedures is shown in comparison with the result of applying conventional CTF correction. The conventional CTF correction, termed CTFR, is equivalent to the application of CTFP+CTFQ. (c) Diagram of the Ewald sphere construction, and how the deviation from the central section, _Δz_⋆, is calculated. The two diffracted beams are shown intersecting the Ewald sphere on the right and left sides of the diagram. The intersection to the left is also shown as its Friedel-related partner, dashed, on the right. The 2_Δz_⋆ distance is the separation of the two Fourier components in reciprocal space.
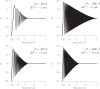
Fig. 2
Simulation of a single-sideband image of an 80 Å particle at - 1.1 µm defocus with only one 3.8 Å Fourier component. The four top panels show four Fourier components in different directions relative to the xy axes, with a uniformly dark region to indicate the shadow of the particle at low frequency. The four middle panels show the result of applying the appropriate CTFP/CTFQ correction. The four bottom panels show the result of applying the conventional CTFR. The bottom panels also show how the fringes are moved in both the correct and incorrect directions, as indicated by the arrowheads. This figure shows a simplistic simulation to demonstrate the effect of the algorithm for single side-band correction. The application of CTFP/CTFQ was carried out using only one sector, rotated by 22° anticlockwise, so that all four 3.8 Å Fourier components would be treated correctly. This creates the diagonal low frequency halo seen in the four middle panels.
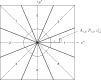
Fig. 3
Proposed multi-sector procedure to allow precise extraction of the Fourier components so that they can be inserted into the 3D transform in their correct position, taking the Ewald sphere curvature into account.
Fig. 4
Application of procedure to an image of a gold nanoparticle in ice. Panels show the raw image of one gold particle with its two approximately Friedel-related diffraction spots, and the image after application of CTFR, CTFP and CTFQ. Application of CTFP/CTFQ was carried out using a single unrotated sector, which creates the low-resolution fringing seen in the bottom two panels. This image (no. 234638) was recorded with 300 keV electrons at 148600 × magnification, and - 1.105 µm defocus on a Falcon 3 detector in integrating movie mode. Arrowheads indicate the location of the 2.35 Å lattice fringes in each image and scale bar is 100 Å.The RMS amplitude at 2.35 Å in Fourier transforms of the regions marked by arrowheads was 257 and 255 in the raw image as well as in CTFP and CTFQ, whereas in CTFR the central RMS amplitude was 246 and the two ghost regions were 125 and 129 (in arbitrary units of intensity, all scaled the same).
Fig. 5
Plot of the weighting function W that takes into account the overlap of the two pseudo-Friedel-related components at lower resolution. There is no overlap for Fourier spacings where ΔF > Dd/2_λ_, so W=1.0 beyond that. At very low resolution, where the two components are largely overlapped, the value of W is equivalent to that of a conventional CTF. The defocus ΔF and the particle size D control the bandwidth of the transition at a given energy, here 300 keV (λ=0.02 Å).
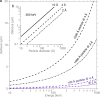
Fig. 6
Plots of the relationship between particle size, defocus and electron energy. Plots show the defocus required (ΔF > Dd/2_λ_) to ensure that all Fourier components from a particle of diameter D, beyond the indicated resolution, d, are completely separated in the image. Panel (a) plots this relationship vs electron energy and (b) shows the dependence on the size of the particle.
Similar articles
- Correction of high-resolution data for curvature of the Ewald sphere.
DeRosier DJ. DeRosier DJ. Ultramicroscopy. 2000 Mar;81(2):83-98. doi: 10.1016/s0304-3991(99)00120-5. Ultramicroscopy. 2000. PMID: 10998793 - A Method for High-Resolution Three-Dimensional Reconstruction with Ewald Sphere Curvature Correction from Transmission Electron Images.
Gureyev TE, Paganin DM, Brown HG, Quiney HM, Allen LJ. Gureyev TE, et al. Microsc Microanal. 2022 Apr 29:1-17. doi: 10.1017/S1431927622000630. Online ahead of print. Microsc Microanal. 2022. PMID: 35485646 - CryoEM single particle reconstruction with a complex-valued particle stack.
Bromberg R, Guo Y, Borek D, Otwinowski Z. Bromberg R, et al. J Struct Biol. 2023 Jun;215(2):107945. doi: 10.1016/j.jsb.2023.107945. Epub 2023 Mar 6. J Struct Biol. 2023. PMID: 36889560 Free PMC article. - A new solution to the curved Ewald sphere problem for 3D image reconstruction in electron microscopy.
Chen JPJ, Schmidt KE, Spence JCH, Kirian RA. Chen JPJ, et al. Ultramicroscopy. 2021 May;224:113234. doi: 10.1016/j.ultramic.2021.113234. Epub 2021 Feb 21. Ultramicroscopy. 2021. PMID: 33652237 - Cryo-EM Structure Determination Using Segmented Helical Image Reconstruction.
Fromm SA, Sachse C. Fromm SA, et al. Methods Enzymol. 2016;579:307-28. doi: 10.1016/bs.mie.2016.05.034. Epub 2016 Jun 28. Methods Enzymol. 2016. PMID: 27572732 Review.
Cited by
- High-resolution reconstruction of a Jumbo-bacteriophage infecting capsulated bacteria using hyperbranched tail fibers.
Ouyang R, Costa AR, Cassidy CK, Otwinowska A, Williams VCJ, Latka A, Stansfeld PJ, Drulis-Kawa Z, Briers Y, Pelt DM, Brouns SJJ, Briegel A. Ouyang R, et al. Nat Commun. 2022 Nov 24;13(1):7241. doi: 10.1038/s41467-022-34972-5. Nat Commun. 2022. PMID: 36433970 Free PMC article. - Interpretation of medium resolution cryoEM maps of multi-protein complexes.
Casañal A, Shakeel S, Passmore LA. Casañal A, et al. Curr Opin Struct Biol. 2019 Oct;58:166-174. doi: 10.1016/j.sbi.2019.06.009. Epub 2019 Jul 27. Curr Opin Struct Biol. 2019. PMID: 31362190 Free PMC article. Review. - Polyelectrolyte coating of cryo-EM grids improves lateral distribution and prevents aggregation of macromolecules.
Hrebík D, Gondová M, Valentová L, Füzik T, Přidal A, Nováček J, Plevka P. Hrebík D, et al. Acta Crystallogr D Struct Biol. 2022 Nov 1;78(Pt 11):1337-1346. doi: 10.1107/S2059798322009299. Epub 2022 Oct 20. Acta Crystallogr D Struct Biol. 2022. PMID: 36322417 Free PMC article. - Near-atomic-scale observation of grain boundaries in a layer-stacked two-dimensional polymer.
Qi H, Sahabudeen H, Liang B, Položij M, Addicoat MA, Gorelik TE, Hambsch M, Mundszinger M, Park S, Lotsch BV, Mannsfeld SCB, Zheng Z, Dong R, Heine T, Feng X, Kaiser U. Qi H, et al. Sci Adv. 2020 Aug 14;6(33):eabb5976. doi: 10.1126/sciadv.abb5976. eCollection 2020 Aug. Sci Adv. 2020. PMID: 32851180 Free PMC article. - Structure of Aquifex aeolicus lumazine synthase by cryo-electron microscopy to 1.42 Å resolution.
Savva CG, Sobhy MA, De Biasio A, Hamdan SM. Savva CG, et al. IUCrJ. 2024 Sep 1;11(Pt 5):723-729. doi: 10.1107/S2052252524005530. IUCrJ. 2024. PMID: 38965901 Free PMC article.
References
- Erickson H.P., Klug A. Measurement and compensation of defocusing and aberrations by Fourier processing of electron micrographs. Phil. Trans. Roy. Soc. Lond. B. 1971;261:105–118.
- Wade R. A brief look at imaging and contrast transfer. Ultramicroscopy. 1992;46:145–156.
- Wolf M., DeRosier D.J., Grigorieff N. Ewald sphere correction for single-particle electron microscopy. Ultramicroscopy. 2006;106:376–382. - PubMed
- Toyoshima C., Unwin P.N.T. Contrast transfer for frozen-hydrated specimens: determination from pairs of defocused images. Ultramicroscopy. 1988;25:279–291. - PubMed
Publication types
Grants and funding
- MC_U105184322/MRC_/Medical Research Council/United Kingdom
- MC_UP_1201/17/MRC_/Medical Research Council/United Kingdom
- U105184322/MRC_/Medical Research Council/United Kingdom
- U105192715/MRC_/Medical Research Council/United Kingdom
LinkOut - more resources
Full Text Sources
Other Literature Sources