Population Structure Promotes the Evolution of Intuitive Cooperation and Inhibits Deliberation - PubMed (original) (raw)
Population Structure Promotes the Evolution of Intuitive Cooperation and Inhibits Deliberation
Mohsen Mosleh et al. Sci Rep. 2018.
Abstract
Spatial structure is one of the most studied mechanisms in evolutionary game theory. Here, we explore the consequences of spatial structure for a question which has received considerable empirical and theoretical attention in recent years, but has not yet been studied from a network perspective: whether cooperation relies on intuitive predispositions or deliberative self-control. We examine this question using a model which integrates the "dual-process" framework from cognitive science with evolutionary game theory, and considers the evolution of agents who are embedded within a social network and only interact with their neighbors. In line with past work in well-mixed populations, we find that selection favors either the intuitive defector strategy which never deliberates, or the dual-process cooperator strategy which intuitively cooperates but uses deliberation to switch to defection when doing so is payoff-maximizing. We find that sparser networks (i.e., smaller average degree) facilitate the success of dual-process cooperators over intuitive defectors, while also reducing the level of deliberation that dual-process cooperators engage in; and that these results generalize across different kinds of networks. These observations demonstrate the important role that spatial structure can have not just on the evolution of cooperation, but on the co-evolution of cooperation and cognition.
Conflict of interest statement
The authors declare no competing interests.
Figures
Figure 1
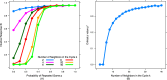
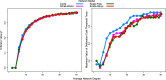
Network structure promotes the evolution of intuitive cooperation: As the density of network connections decreases, it becomes easier for selection to favor intuitive cooperators. Shown is the average intuitive response (S i, probability of playing TFT) across different values of p (probability of repeated games) for cycles with different number of neighbors (k) for each node. (A) S i for six representative values of k across the full range of p. (B) Critical value of p at which S i = 0.5 across the full range of k. As k decreases, the transition from S i = 0 to S i = 1 occurs at lower values of p.
Figure 2
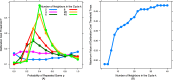
Network structure reduces the amount of deliberation: As the density of network connections decreases, the maximum cost agents are willing to pay to deliberation decreases. (A) Cost threshold of deliberation (T) for six representative values of k across the full range of probabilities of repeated game (p), (B) maximum value of cost threshold of deliberation over all p values (T max) as a function of number of neighbors in the cycle (k). As k decreases, dual process cooperators engage in less deliberation (T max decreases).
Figure 3
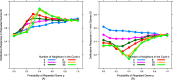
Network structure has little qualitative impact on deliberative responses in repeated games, but promotes deliberative cooperation in one-shot games. (A) Deliberative response in repeated games (S r) and (B) Deliberative response in 1-shot games (S 1) across different values of probability of repeated game (p) for different number of neighbors in the cycle (k).
Figure 4
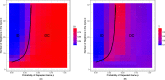
Dual-process cooperators evolve when it is sufficiently likely that games are repeated and/or the network is sufficiently sparse. (A) Probability of intuitive cooperation (S i) and (B) cost threshold of deliberation (T) as a function of number of neighbors in the cycle (k) and probability of repeated game (p). The black lines in both panels represent the value of k and p at which the dominant strategy transitions from ID to DC. There are only two dominant strategies: for high values of k and low values of p the intuitive defectors (ID) who never deliberate are dominant, while for low values of k and high values of p the dual-process cooperator (DC) strategy dominates. Lower value of k makes it easier for the DC strategy to succeed, and reduces the amount of deliberation DC agents are willing to engage in.
Figure 5
Similar evolutionary dynamics are observed across varying network structures. (A) Critical value of probability of repeated game p at which S i = 0.5 and, (B) Maximum value of cost threshold of deliberation T over all values of p, across average network degree k for Cycle, Watts-Strogatz Small-World, Barabási-Albert Scale-Free, and Erdős-Rényi random networks. Results obtained for cycles are robust to networks with heterogeneous degree suggesting that the effect of structure on the coevolution of cooperation and cognition is mainly driven by the sparsity of connections within the network.
Similar articles
- Intuition, deliberation, and the evolution of cooperation.
Bear A, Rand DG. Bear A, et al. Proc Natl Acad Sci U S A. 2016 Jan 26;113(4):936-41. doi: 10.1073/pnas.1517780113. Epub 2016 Jan 11. Proc Natl Acad Sci U S A. 2016. PMID: 26755603 Free PMC article. - Co-evolution of cooperation and cognition: the impact of imperfect deliberation and context-sensitive intuition.
Bear A, Kagan A, Rand DG. Bear A, et al. Proc Biol Sci. 2017 Mar 29;284(1851):20162326. doi: 10.1098/rspb.2016.2326. Proc Biol Sci. 2017. PMID: 28330915 Free PMC article. - Transforming the dilemma.
Taylor C, Nowak MA. Taylor C, et al. Evolution. 2007 Oct;61(10):2281-92. doi: 10.1111/j.1558-5646.2007.00196.x. Epub 2007 Aug 17. Evolution. 2007. PMID: 17711471 Free PMC article. - Cooperation in a generalized age-structured spatial game.
Souza PVS, Silva R, Bauch C, Girardi D. Souza PVS, et al. J Theor Biol. 2020 Jan 7;484:109995. doi: 10.1016/j.jtbi.2019.109995. Epub 2019 Sep 3. J Theor Biol. 2020. PMID: 31491496 Review. - The dual-process approach to human sociality: Meta-analytic evidence for a theory of internalized heuristics for self-preservation.
Capraro V. Capraro V. J Pers Soc Psychol. 2024 May;126(5):719-757. doi: 10.1037/pspa0000375. Epub 2024 Jan 15. J Pers Soc Psychol. 2024. PMID: 38227465 Review.
Cited by
- Globalization and the rise and fall of cognitive control.
Mosleh M, Kyker K, Cohen JD, Rand DG. Mosleh M, et al. Nat Commun. 2020 Jun 18;11(1):3099. doi: 10.1038/s41467-020-16850-0. Nat Commun. 2020. PMID: 32555322 Free PMC article. - Cooperation without punishment.
Battu B, Rahwan T. Battu B, et al. Sci Rep. 2023 Jan 21;13(1):1213. doi: 10.1038/s41598-023-28372-y. Sci Rep. 2023. PMID: 36681708 Free PMC article. - Cognitive reflection correlates with behavior on Twitter.
Mosleh M, Pennycook G, Arechar AA, Rand DG. Mosleh M, et al. Nat Commun. 2021 Feb 10;12(1):921. doi: 10.1038/s41467-020-20043-0. Nat Commun. 2021. PMID: 33568667 Free PMC article. - Coevolution between the cost of decision and the strategy contributes to the evolution of cooperation.
Ohdaira T. Ohdaira T. Sci Rep. 2019 Mar 14;9(1):4465. doi: 10.1038/s41598-019-41073-9. Sci Rep. 2019. PMID: 30872729 Free PMC article.
References
- Jagau, S. & van Veelen, M. A general evolutionary framework for the role of intuition and deliberation in cooperation. 1, 0152 (2017).
- Bear A, Rand DG. The value of information. Nature Human Behavior. 2017;1:1–2.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous