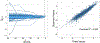Algorithms for Fitting the Constrained Lasso - PubMed (original) (raw)
Algorithms for Fitting the Constrained Lasso
Brian R Gaines et al. J Comput Graph Stat. 2018.
Abstract
We compare alternative computing strategies for solving the constrained lasso problem. As its name suggests, the constrained lasso extends the widely-used lasso to handle linear constraints, which allow the user to incorporate prior information into the model. In addition to quadratic programming, we employ the alternating direction method of multipliers (ADMM) and also derive an efficient solution path algorithm. Through both simulations and benchmark data examples, we compare the different algorithms and provide practical recommendations in terms of efficiency and accuracy for various sizes of data. We also show that, for an arbitrary penalty matrix, the generalized lasso can be transformed to a constrained lasso, while the converse is not true. Thus, our methods can also be used for estimating a generalized lasso, which has wide-ranging applications. Code for implementing the algorithms is freely available in both the Matlab toolbox SparseReg and the Julia package ConstrainedLasso. Supplementary materials for this article are available online.
Keywords: Alternating direction method of multipliers; Convex optimization; Generalized lasso; Linear constraints; Penalized regression; Regularization path.
Figures
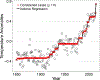
Figure 1:
Isotonic regression fit shows a monotone trend in temperature abnormalities. The constrained lasso solution at ρ = 0 is identical to isotonic regression.
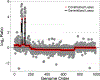
Figure 2:
Different simulation settings show consistently comparable or superior performance of the path algorithm whereas performances of ADMM and QP vary depending on the size and complexity of the problem. The runtimes for the solution path algorithm are averaged across the number of kinks in the path to make the runtimes more comparable to the other algorithms estimated at one value of the tuning parameter, ρ = _ρ_scale · _ρ_max.
Figure 3:
Generalized lasso and constrained lasso produce identical sparse fused lasso estimates on the brain tumor data
Figure 4:
Path algorithm yields the constrained lasso solution path for the Ames housing data with 48 factors. The dashed line marks the model with the lowest BIC (left panel) as well as the identity line (right panel). Here the response is the log-transformed sale price that is standardized to have mean 0 and standard deviation 1.
Similar articles
- A fast solution to the lasso problem with equality constraints.
Tran L, Li G, Luo L, Jiang H. Tran L, et al. J Comput Graph Stat. 2024;33(3):804-813. doi: 10.1080/10618600.2023.2277877. Epub 2023 Dec 26. J Comput Graph Stat. 2024. PMID: 39465000 Free PMC article. - A Path Algorithm for Constrained Estimation.
Zhou H, Lange K. Zhou H, et al. J Comput Graph Stat. 2013;22(2):261-283. doi: 10.1080/10618600.2012.681248. J Comput Graph Stat. 2013. PMID: 24039382 Free PMC article. - A New Algorithm and Theory for Penalized Regression-based Clustering.
Wu C, Kwon S, Shen X, Pan W. Wu C, et al. J Mach Learn Res. 2016;17:188. J Mach Learn Res. 2016. PMID: 31662706 Free PMC article. - [Generalized interaction LASSO based on alternating direction method of multipliers for liver disease classification].
Li J, Tong X, Wang J. Li J, et al. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2017 Jun 1;34(3):350-356. doi: 10.7507/1001-5515.201508026. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2017. PMID: 29745499 Free PMC article. Chinese. - Constrained Pulse Radar Waveform Design Based on Optimization Theory.
Wu J, Zhang J, Chen Y. Wu J, et al. Sensors (Basel). 2025 Feb 16;25(4):1203. doi: 10.3390/s25041203. Sensors (Basel). 2025. PMID: 40006434 Free PMC article. Review.
Cited by
- A PET/CT radiomics model for predicting distant metastasis in early-stage non-small cell lung cancer patients treated with stereotactic body radiotherapy: a multicentric study.
Yu L, Zhang Z, Yi H, Wang J, Li J, Wang X, Bai H, Ge H, Zheng X, Ni J, Qi H, Guan Y, Xu W, Zhu Z, Xing L, Dekker A, Wee L, Traverso A, Ye Z, Yuan Z. Yu L, et al. Radiat Oncol. 2024 Jan 22;19(1):10. doi: 10.1186/s13014-024-02402-z. Radiat Oncol. 2024. PMID: 38254106 Free PMC article. - Interactions Between Donor Age and 12-Month Estimated Glomerular Filtration Rate on Allograft and Patient Outcomes After Kidney Transplantation.
Lim WH, Ooi E, Pilmore HL, Johnson DW, McDonald SP, Clayton P, Hawley C, Mulley WR, Francis R, Collins MG, Jaques B, Larkins NG, Davies CE, Wyburn K, Chadban SJ, Wong G. Lim WH, et al. Transpl Int. 2022 Feb 7;35:10199. doi: 10.3389/ti.2022.10199. eCollection 2022. Transpl Int. 2022. PMID: 35185379 Free PMC article. - Application of a neural interface for restoration of leg movements: Intra-spinal stimulation using the brain electrical activity in spinally injured rabbits.
Heravi MAY, Maghooli K, Nowshiravan Rahatabad F, Rezaee R. Heravi MAY, et al. J Appl Biomed. 2020 Aug;18(2-3):33-40. doi: 10.32725/jab.2020.009. Epub 2020 Jun 26. J Appl Biomed. 2020. PMID: 34907723 - A fast solution to the lasso problem with equality constraints.
Tran L, Li G, Luo L, Jiang H. Tran L, et al. J Comput Graph Stat. 2024;33(3):804-813. doi: 10.1080/10618600.2023.2277877. Epub 2023 Dec 26. J Comput Graph Stat. 2024. PMID: 39465000 Free PMC article. - Penalized and constrained LAD estimation in fixed and high dimension.
Wu X, Liang R, Yang H. Wu X, et al. Stat Pap (Berl). 2022;63(1):53-95. doi: 10.1007/s00362-021-01229-0. Epub 2021 Mar 31. Stat Pap (Berl). 2022. PMID: 33814727 Free PMC article.
References
- Altenbuchinger M, Rehberg T, Zacharias H, Stämmler F, Dettmer K, Weber D, Hiergeist A, Gessner A, Holler E, Oefner PJ, et al. (2017), “Reference point insensitive molecular data analysis,” Bioinformatics, 33, 219–226. - PubMed
- Arnold TB and Tibshirani RJ (2014), genlasso: Path Algorithm for Generalized Lasso Problems, R package version 1.3.
- Arnold TB (2016), “Efficient Implementations of the Generalized Lasso Dual Path Algorithm,” Journal of Computational and Graphical Statistics, 25, 1–27.
- Boyd S, Parikh N, Chu E, Peleato B, and Eckstein J (2011), “Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers,” Foundations and Trends in Machine Learning, 3, 1–122.
- Bredel M, Bredel C, Juric D, Harsh GR, Vogel H, Recht LD, and Sikic BI (2005), “High-Resolution Genome-Wide Mapping of Genetic Alterations in Human Glial Brain Tumors,” Cancer Research, 65, 4088–4096. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials