Coevolution between the cost of decision and the strategy contributes to the evolution of cooperation - PubMed (original) (raw)
Coevolution between the cost of decision and the strategy contributes to the evolution of cooperation
Tetsushi Ohdaira. Sci Rep. 2019.
Abstract
Cooperation is still an important issue for both evolutionary and social scientists. There are some remarkable methods for sustaining cooperation. On the other hand, various studies discuss whether human deliberative behaviour promotes or inhibits cooperation. As those studies of human behaviour develop, in the study of evolutionary game theory, models considering deliberative behaviour of game players are increasing. Based on that trend, the author considers that decision of a person requires certain time and imposes a psychological burden on him/her and defines such burden as the cost of decision. This study utilizes the model of evolutionary game theory that each player plays the spatial prisoner's dilemma game with opponent players connected to him/her and introduces the cost of decision. The main result of this study is that the introduction of the cost of decision contributes to the evolution of cooperation, although there are some differences in the extent of its contribution regarding the three types of sparse topology of connections. Regarding the distribution of the cost of decision, especially in the case of the scale-free topology of connections, players with high cost of decision, which seem to be disadvantageous at first glance, sometimes become mainstream at the last.
Conflict of interest statement
The author declares no competing interests.
Figures
Figure 1
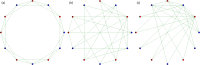
This figure is Fig. 1 of the previous study. Three panels (a), (b), and (c) show the (a) regular, (b) random, and (c) scale free topology of connections in the case of <_k_> = 4. Each topology is defined as one dimensional lattices of periodic boundary conditions, and a vertex represents a player. Cooperators are shown in blue, and defectors are shown in red. Although the model of this study has N = 1000 players, this figure has only 12 players to make each topology easy to understand.
Figure 2
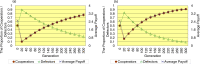
This figure shows the time series results of the proportion of cooperators (left vertical axis), the proportion of defectors (left vertical axis), and the average payoff of all players (right vertical axis) regarding the regular topology of connections (a) without/(b) with the cost of decision (error bars: SE, standard errors).
Figure 3
This figure shows the time series results of the proportion of cooperators (left vertical axis), the proportion of defectors (left vertical axis), and the average payoff of all players (right vertical axis) regarding the random topology of connections (a) without/(b) with the cost of decision (error bars: SE, standard errors).
Figure 4
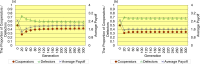
This figure shows the time series results of the proportion of cooperators (left vertical axis), the proportion of defectors (left vertical axis), and the average payoff of all players (right vertical axis) regarding the scale-free topology of connections (a,c) without/(b,d) with the cost of decision (error bars: SE, standard errors). The upper row indicates the results that defectors become dominant, while the lower row depicts the results that cooperators become dominant.
Figure 5
This figure shows how many players have the cost of decision (D(i)) of each range when the topology of connections is regular (a,b), random (c,d), and scale-free (e,f). Panels of the left column (a,c,e) indicate the results of Simulations from 1 to 10, and those of the right column (b,d,f) depict the results of Simulations from 11 to 20. When the topology of connections is scale-free (e,f), defectors-dominant simulation runs in the last 300 generation are Simulations 1, 2, 4, 5, 9, 10, 13, 14, 18, and 20, while cooperators-dominant simulation runs in the last 300 generation are Simulations 3, 6, 7, 8, 11, 12, 15, 16, 17, and 19.
Figure 6
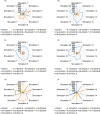
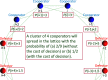
This figure explains the probability that a cluster of 4 cooperators will spread regarding both cases (a) without/(b) with the cost of decision.
Similar articles
- Evolutionary prisoner's dilemma on evolving random networks.
Xu Z, Le Y, Zhang L. Xu Z, et al. Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Apr;89(4):042142. doi: 10.1103/PhysRevE.89.042142. Epub 2014 Apr 28. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 24827227 - Difference of reciprocity effect in two coevolutionary models of presumed two-player and multiplayer games.
Tanimoto J. Tanimoto J. Phys Rev E Stat Nonlin Soft Matter Phys. 2013 Jun;87(6):062136. doi: 10.1103/PhysRevE.87.062136. Epub 2013 Jun 25. Phys Rev E Stat Nonlin Soft Matter Phys. 2013. PMID: 23848656 - Evolution of extortion in structured populations.
Szolnoki A, Perc M. Szolnoki A, et al. Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Feb;89(2):022804. doi: 10.1103/PhysRevE.89.022804. Epub 2014 Feb 14. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25353531 - Cooperation in a generalized age-structured spatial game.
Souza PVS, Silva R, Bauch C, Girardi D. Souza PVS, et al. J Theor Biol. 2020 Jan 7;484:109995. doi: 10.1016/j.jtbi.2019.109995. Epub 2019 Sep 3. J Theor Biol. 2020. PMID: 31491496 Review. - The role of evolutionary game theory in spatial and non-spatial models of the survival of cooperation in cancer: a review.
Coggan H, Page KM. Coggan H, et al. J R Soc Interface. 2022 Aug;19(193):20220346. doi: 10.1098/rsif.2022.0346. Epub 2022 Aug 17. J R Soc Interface. 2022. PMID: 35975562 Free PMC article. Review.
Cited by
- A moderated-mediation analysis of performance appraisal politics perception and counterproductive work behavior.
Wang HY, Chen ZX. Wang HY, et al. Front Psychol. 2022 Oct 25;13:928923. doi: 10.3389/fpsyg.2022.928923. eCollection 2022. Front Psychol. 2022. PMID: 36389510 Free PMC article. - Cooperation without punishment.
Battu B, Rahwan T. Battu B, et al. Sci Rep. 2023 Jan 21;13(1):1213. doi: 10.1038/s41598-023-28372-y. Sci Rep. 2023. PMID: 36681708 Free PMC article.
References
- Chen X, Szolnoki A, Perc M. Probabilistic sharing solves the problem of costly punishment. New J. Phys. 2014;16:083016. doi: 10.1088/1367-2630/16/8/083016. - DOI
- Wang Q, He N, Chen X. Replicator dynamics for public goods game with resource allocation in large populations. Appl. Math. Comput. 2018;328:162–170. doi: 10.1016/j.amc.2018.01.045. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials