Upgraded Giant Metrewave Radio Telescope timing of NGC 1851A: a possible millisecond pulsar - neutron star system - PubMed (original) (raw)
Upgraded Giant Metrewave Radio Telescope timing of NGC 1851A: a possible millisecond pulsar - neutron star system
A Ridolfi et al. Mon Not R Astron Soc. 2019 Dec.
Abstract
In this work, we present the results of 1 yr of upgraded Giant Metrewave Radio Telescope timing measurements of PSR J0514-4002A, a 4.99-ms pulsar in a 18.8-d eccentric ([Formula: see text]) orbit with a massive companion located in the globular cluster NGC 1851. Combining these data with earlier Green Bank Telescope data, we greatly improve the precision of the rate of advance of periastron, [Formula: see text] which, assuming the validity of general relativity, results in a much refined measurement of the total mass of the binary, [Formula: see text]. Additionally, we measure the Einstein delay parameter, γ, something that has never been done for any binary system with an orbital period larger than [Formula: see text]10 h. The measured value, [Formula: see text], is by far the largest for any binary pulsar. Furthermore, we measure the proper motion of the system ([Formula: see text] and [Formula: see text]), which is not only important for analysing its motion in the cluster, but is also essential for a proper interpretation of γ, given the latter parameter's correlation with the variation of the projected semimajor axis. The measurements of γ and the proper motion enable a separation of the system component masses: we obtain a pulsar mass of [Formula: see text] and a companion mass of [Formula: see text]. This raises the possibility that the companion is also a neutron star. Searches for radio pulsations from the companion have thus far been unsuccessful; hence, we cannot confirm the latter hypothesis. The low mass of this millisecond pulsar - one of the lowest ever measured for such objects - clearly indicates that the recycling process can be achieved with a relatively small amount of mass transfer.
Keywords: (Galaxy:) globular clusters: individual (NGC 1851); (stars:) binaries: general; (stars:) pulsars: general; (stars:) pulsars: individual: PSR J0514−4002A; stars: neutron.
© 2019 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society.
Figures
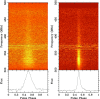
Figure 1.
Observation of NGC 1851A as taken with the 250–500 MHz (Band 3) receiver of the uGMRT on 2017 November 14 simultaneously in PA mode (left) and CDP mode (right). Top panels: Intensity as a function of pulse phase (_x_-axis) and observing radio frequency (_y_-axis). Bottom panels: Corresponding integrated pulse profile. Thanks to the CDP available in CDP mode, the pulse profile of NGC 1851A is much narrower than in PA mode, resulting in far more precise timing. Radio frequency interference from the Mobile User Objective System (MUOS) satellite system is visible in the 360–380 MHz band.
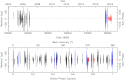
Figure 2.
Timing residuals for NGC 1851A, obtained with the DDFWHE timing solution listed in Table 2. Top: ToA residuals as a function of the epoch, with the 10-yr gap in observations evident. Bottom: ToA residuals as a function of the orbital phase, with phase 0 denoting periastron. The residual 1σ uncertainties are indicated by vertical error bars. Black indicates the earlier GBT timing, blue the uGMRT data taken in PA mode, and red the uGMRT data in CDP mode. Note the marked improvement of the CDP data compared to the PA mode.
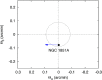
Figure 3.
Position of NGC 1851A with respect to the nominal centre of the cluster, located at α = and δ =
(Gaia Collaboration et al. 2018). The dashed circle shows the core radius of NGC 1851, which is 0.09 arcmin, according to Harris (, 2010 edition). The blue arrow indicates the direction of the projected motion of the pulsar relative to the cluster.
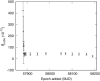
Figure 4.
Orbital period derivative () of NGC 1851A measured using the DDFWHE binary model as a function of epoch added from uGMRT data set (the GBT data set is also always included in the fit). The last point, which is the one derived using the whole GBT+uGMRT data set, is the value reported in Table 2.
Figure 5.
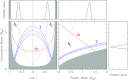
Mass constraints for PSR J0514−4002A. In the main square plots, the lines indicate the regions that are (according to general relativity) consistent with the nominal and measurements of
(solid red), γ (solid blue), and _h_3 (grey) obtained from the DDFWHE model (see Table 2). For the _h_3 estimate, we assumed the value of ς marked by the dotted grey lines (Section 3.10); only the nominal (near
) and
lines are visible; the latter excludes orbital inclinations near
. In the left plot, we display cos i (for randomly inclined orbits this would have equal probability) versus the companion mass (_M_c); the grey region is excluded by the mass function of the system – the pulsar mass (_M_p) must be larger than 0. In the right plot, we display _M_p versus _M_c; the grey region is excluded by the constraint
. The side panels display the 1d pdfs for cos i (top left), _M_p (top right) and _M_c (right), normalized to the maximum (for details, see Section 4). The distribution for _M_c is derived from the distribution for _M_c using
.
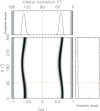
Figure 6.
Central panel: The full cos _i_–Ω space for binary pulsars. For PSR J0514−4002A, the grey regions are excluded by the requirement that the pulsar mass must be larger than 0. The dotted orange line indicates the position angle of the proper motion of the system. The grey-scale indicates the probability density, with zero indicated by white and maximum probability density indicated by black. As we can see, the best orbital inclination varies significantly with Ω. Top panel: Probability density function for cos i, normalized to the maximum. Right-hand panel: Probability density function for Ω. This is almost uniform; that is, this variable is not constrained for this system.
Similar articles
- A binary pulsar in a 53-minute orbit.
Pan Z, Lu JG, Jiang P, Han JL, Chen HL, Han ZW, Liu K, Qian L, Xu RX, Zhang B, Luo JT, Yan Z, Yang ZL, Zhou DJ, Wang PF, Wang C, Li MH, Zhu M. Pan Z, et al. Nature. 2023 Aug;620(7976):961-964. doi: 10.1038/s41586-023-06308-w. Epub 2023 Jun 20. Nature. 2023. PMID: 37339734 Free PMC article. - A pulsar in a binary with a compact object in the mass gap between neutron stars and black holes.
Barr ED, Dutta A, Freire PCC, Cadelano M, Gautam T, Kramer M, Pallanca C, Ransom SM, Ridolfi A, Stappers BW, Tauris TM, Venkatraman Krishnan V, Wex N, Bailes M, Behrend J, Buchner S, Burgay M, Chen W, Champion DJ, Chen CR, Corongiu A, Geyer M, Men YP, Padmanabh PV, Possenti A. Barr ED, et al. Science. 2024 Jan 19;383(6680):275-279. doi: 10.1126/science.adg3005. Epub 2024 Jan 18. Science. 2024. PMID: 38236981 - A test of general relativity from the three-dimensional orbital geometry of a binary pulsar.
van Straten W, Bailes M, Britton M, Kulkarni SR, Anderson SB, Manchester RN, Sarkissian J. van Straten W, et al. Nature. 2001 Jul 12;412(6843):158-60. doi: 10.1038/35084015. Nature. 2001. PMID: 11449265 - Binary and Millisecond Pulsars.
Lorimer DR. Lorimer DR. Living Rev Relativ. 2008;11(1):8. doi: 10.12942/lrr-2008-8. Epub 2008 Nov 4. Living Rev Relativ. 2008. PMID: 28179824 Free PMC article. Review. - The prospects of pulsar timing with new-generation radio telescopes and the Square Kilometre Array.
Stappers BW, Keane EF, Kramer M, Possenti A, Stairs IH. Stappers BW, et al. Philos Trans A Math Phys Eng Sci. 2018 May 28;376(2120):20170293. doi: 10.1098/rsta.2017.0293. Philos Trans A Math Phys Eng Sci. 2018. PMID: 29661980 Review.
References
- Antoniadis J., van Kerkwijk M. H., Koester D., Freire P. C. C., Wex N., Tauris T. M., Kramer M., Bassa C. G., 2012, MNRAS, 423, 3316.10.1111/j.1365-2966.2012.21124.x - DOI
- Arzoumanian Z. et al. ., 2018, ApJS, 235, 37.10.3847/1538-4365/aab5b0 - DOI
- Barker B. M., O’Connell R. F., 1975, Phys. Rev. D, 12, 329.10.1103/PhysRevD.12.329 - DOI
- Baumgardt H., Hilker M., 2018, MNRAS, 478, 1520.10.1093/mnras/sty1057 - DOI
- Blandford R., Teukolsky S. A., 1976, ApJ, 205, 580.10.1086/154315 - DOI
LinkOut - more resources
Full Text Sources