Uncomputability and complexity of quantum control - PubMed (original) (raw)
Uncomputability and complexity of quantum control
Denys I Bondar et al. Sci Rep. 2020.
Abstract
In laboratory and numerical experiments, physical quantities are known with a finite precision and described by rational numbers. Based on this, we deduce that quantum control problems both for open and closed systems are in general not algorithmically solvable, i.e., there is no algorithm that can decide whether dynamics of an arbitrary quantum system can be manipulated by accessible external interactions (coherent or dissipative) such that a chosen target reaches a desired value. This conclusion holds even for the relaxed requirement of the target only approximately attaining the desired value. These findings do not preclude an algorithmic solvability for a particular class of quantum control problems. Moreover, any quantum control problem can be made algorithmically solvable if the set of accessible interactions (i.e., controls) is rich enough. To arrive at these results, we develop a technique based on establishing the equivalence between quantum control problems and Diophantine equations, which are polynomial equations with integer coefficients and integer unknowns. In addition to proving uncomputability, this technique allows to construct quantum control problems belonging to different complexity classes. In particular, an example of the control problem involving a two-mode coherent field is shown to be NP-hard, contradicting a widely held believe that two-body problems are easy.
Conflict of interest statement
The authors declare no competing interests.
Figures
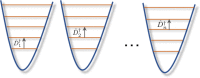
Figure 1
A physical system for simulating Diophantine equations with n variables. The system is either n trapped ions or an _n_–mode coherent field. The controls Dˆ1†, …, Dˆn† independently address each subsystem. For ions, the controls excite transitions between nearest levels, and transfer population of the highest excited state down to the ground state. For coherent states, the control for the _i_-th mode is the displacement Dˆi by the magnitude one. The Diophantine polynomial is embedded in the observable Oˆ whose expectation value has to be optimized as the control goal. A highly non-trivial example corresponds already to the simple case of a two-mode coherent field (n = 2) with Oˆ=−(αaˆ1†aˆ1†+βaˆ2†−γ)(αaˆ1aˆ1+βaˆ2−γ), where α, β, and γ are positive integers. The observable is non-linear but physical; its leading term is of the Kerr-type nonlinearity. Maximizing the expectation of this observable is NP-hard, i.e., it is at least as hard as the famous Traveling Salesman Problem. Note that an n = 9 system is sufficient to solve any Diophantine equation.
Similar articles
- P/NP, and the quantum field computer.
Freedman MH. Freedman MH. Proc Natl Acad Sci U S A. 1998 Jan 6;95(1):98-101. doi: 10.1073/pnas.95.1.98. Proc Natl Acad Sci U S A. 1998. PMID: 9419335 Free PMC article. - Optimization of the multivariate polynomial public key for quantum safe digital signature.
Kuang R, Perepechaenko M. Kuang R, et al. Sci Rep. 2023 Apr 19;13(1):6363. doi: 10.1038/s41598-023-32461-3. Sci Rep. 2023. PMID: 37076506 Free PMC article. - Computational complexity and fundamental limitations to fermionic quantum Monte Carlo simulations.
Troyer M, Wiese UJ. Troyer M, et al. Phys Rev Lett. 2005 May 6;94(17):170201. doi: 10.1103/PhysRevLett.94.170201. Epub 2005 May 4. Phys Rev Lett. 2005. PMID: 15904269 - Factoring semi-primes with (quantum) SAT-solvers.
Mosca M, Verschoor SR. Mosca M, et al. Sci Rep. 2022 May 14;12(1):7982. doi: 10.1038/s41598-022-11687-7. Sci Rep. 2022. PMID: 35568707 Free PMC article. - Hybrid schemes based on quantum mechanics/molecular mechanics simulations goals to success, problems, and perspectives.
Ferrer S, Ruiz-Pernía J, Martí S, Moliner V, Tuñón I, Bertrán J, Andrés J. Ferrer S, et al. Adv Protein Chem Struct Biol. 2011;85:81-142. doi: 10.1016/B978-0-12-386485-7.00003-X. Adv Protein Chem Struct Biol. 2011. PMID: 21920322 Review.
References
- Glaser, S. J. et al. Training Schrödinger’s cat: quantum optimal control. Eur. Phys. J. D 69, 279, ISSN 1434-6079, 10.1140/epjd/e2015-60464-1 (2015).
- Butkovskiy, A. G. & Samoilenko, Y. I. Control of Quantum-Mechanical Processes and Systems (Kluwer Academic, Dordrecht, 1990).
- Shapiro, M. & Brumer, P. Principles of the quantum control of molecular processes (Wiley-VCH, 2003).
- Tannor, D. J. Introduction to quantum mechanics: a time-dependent perspective (University Science Books, 2007).
- Fradkov, A. Cybernetical Physics: From Control of Chaos to Quantum Control (Springer, New York, 2007).
LinkOut - more resources
Full Text Sources
Miscellaneous