From Local Explanations to Global Understanding with Explainable AI for Trees - PubMed (original) (raw)
From Local Explanations to Global Understanding with Explainable AI for Trees
Scott M Lundberg et al. Nat Mach Intell. 2020 Jan.
Abstract
Tree-based machine learning models such as random forests, decision trees, and gradient boosted trees are popular non-linear predictive models, yet comparatively little attention has been paid to explaining their predictions. Here, we improve the interpretability of tree-based models through three main contributions: 1) The first polynomial time algorithm to compute optimal explanations based on game theory. 2) A new type of explanation that directly measures local feature interaction effects. 3) A new set of tools for understanding global model structure based on combining many local explanations of each prediction. We apply these tools to three medical machine learning problems and show how combining many high-quality local explanations allows us to represent global structure while retaining local faithfulness to the original model. These tools enable us to i) identify high magnitude but low frequency non-linear mortality risk factors in the US population, ii) highlight distinct population sub-groups with shared risk characteristics, iii) identify non-linear interaction effects among risk factors for chronic kidney disease, and iv) monitor a machine learning model deployed in a hospital by identifying which features are degrading the model's performance over time. Given the popularity of tree-based machine learning models, these improvements to their interpretability have implications across a broad set of domains.
Figures
Figure 1:. Local explanations based on TreeExplainer enable a wide variety of new ways to understand global model structure.
(a) A local explanation based on assigning a numeric measure of credit to each input feature. (b) By combining many local explanations, we can represent global structure while retaining local faithfulness to the original model. We demonstrate this by using three medical datasets to train gradient boosted decision trees and then compute local explanations based on SHapley Additive exPlanation (SHAP) values [3]. Computing local explanations across all samples in a dataset enables development of many tools for understanding global model structure.
Figure 2:. Gradient boosted tree models can be more accurate than neural networks and more interpretable than linear models.
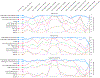
(a) Gradient boosted tree models outperform both linear models and neural networks on all our medical datasets, where (**) represents a bootstrap retrain P-value < 0.01, and (*) represents a P-value of 0.03. (b–d) Linear models exhibit explanation and accuracy error in the presence of non-linearity. (b) The data generating models we used for the simulation ranged from linear to quadratic along the body mass index (BMI) dimension. (c) Linear logistic regression (red) outperformed gradient boosting (blue) up to a specific amount of non-linearity. Not surprisingly, the linear model’s bias is higher than the gradient boosting model’s, as shown by the steeper slope as we increase non-linearity. (d) As the true function becomes more non-linear, the linear model assigns more credit (coefficient weight) to features that were not used by the data generating model. The weight placed on these irrelevant features is driven by complex cancellation effects and so is not readily interpretable (Supplementary Figure 1). Furthermore, adding L1 regularization to the linear model does not solve the problem (Supplementary Figures 2 and 3).
Figure 3:. Explanation method performance across 15 different evaluation metrics and three classification models in the chronic kidney disease dataset.
Each column represents an evaluation metric, and each row represents an explanation method. The scores for each metric are scaled between the minimum and maximum value, and methods are sorted by their average score. TreeExplainer outperforms previous approaches not only by having theoretical guarantees about consistency, but also by exhibiting improved performance across a large set of quantitative metrics that measure explanation quality (Methods). When these experiments were repeated for two synthetic datasets, TreeExplainer remained the top-performing method (Supplementary Figures 6 and 7). Note that, as predicted, Saabas better approximates the Shapley values (and so becomes a better attribution method) as the number of trees increases (Methods). *Since MAPLE models the local gradient of a function, and not the impact of hiding a feature, it tends to perform poorly on these feature importance metrics [35].
Figure 4:. By combining many local explanations, we can provide rich summaries of both an entire model and individual features.
Explanations are based on a gradient boosted decision tree model trained on the mortality dataset. (a) (left) bar-chart of the average SHAP value magnitude, and (right) a set of beeswarm plots, where each dot corresponds to an individual person in the study. The dot’s position on the x-axis shows the impact that feature has on the model’s prediction for that person. When multiple dots land at the same x position, they pile up to show density. (b) SHAP dependence plot of systolic blood pressure vs. its SHAP value in the mortality model. A clear interaction effect with age is visible, which increases the impact of early onset high blood pressure. (c) Using SHAP interaction values to remove the interaction effect of age from the model. (d) Plot of just the interaction effect of systolic blood pressure with age; shows how the effect of systolic blood pressure on mortality risk varies with age. Adding the y-values of C and D produces B. (e) A dependence plot of systolic blood pressure vs. its SHAP value in the kidney model; shows an increase in kidney disease risk at a systolic blood pressure of 125 (which parallels the increase in mortality risk). (f) Plot of the SHAP interaction value of ‘white blood cells’ with ‘blood urea nitrogen’; shows that high white blood cell counts increase the negative risk conferred by high blood urea nitrogen. (g) Plot of the SHAP interaction value of sex vs. age in the mortality model; shows how the differential risk for men and women changes over a lifetime.
Figure 5:. Monitoring plots reveal problems that would otherwise be invisible in a retrospective hospital machine learning model deployment.
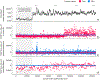
(a) The squared error of a hospital duration model averaged over the nearest 1,000 samples. The increase in error after training occurs because the test error is (as expected) higher than the training error. (b) The SHAP value of the model loss for the feature that indicates whether the procedure happens in room 6. A significant change occurs when we intentionally swap the labels of rooms 6 and 13, which is invisible in the overall model loss. (c) The SHAP value of the model loss for the general anesthesia feature; the spike one-third of the way into the data results from previously unrecognized transient data corruption at a hospital. (d) The SHAP value of the model loss for the atrial fibrillation feature. The plot’s upward trend shows feature drift over time (P-value 5.4 × 10−19).
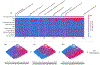
Figure 6:. Local explanation embeddings support both supervised clustering and interpretable dimensionality reduction.
(A) A clustering of mortality study individuals by their local explanation embedding. Columns are patients, and rows are features’ normalized SHAP values. Sorting by a hierarchical clustering reveals population subgroups that have distinct mortality risk factors. (B–D) A local explanation embedding of kidney study visits projected onto two principal components. Local feature attribution values can be viewed as an embedding of the samples into a space where each dimension corresponds to a feature and all axes have the units of the model’s output. The embedding colored by: (B) the predicted log odds of a participant developing end-stage renal disease within 4 years of that visit, (C) the SHAP value of blood creatinine, and (D) the SHAP value of the urine protein/creatinine ratio. Many other features also align with these top two principal components (Supplementary Figure 13), and an equivalent unsupervised PCA embedding is far less interpretable (Supplementary Figure 14)
Similar articles
- Interpretable machine learning with tree-based shapley additive explanations: Application to metabolomics datasets for binary classification.
Bifarin OO. Bifarin OO. PLoS One. 2023 May 4;18(5):e0284315. doi: 10.1371/journal.pone.0284315. eCollection 2023. PLoS One. 2023. PMID: 37141218 Free PMC article. - Why did AI get this one wrong? - Tree-based explanations of machine learning model predictions.
Parimbelli E, Buonocore TM, Nicora G, Michalowski W, Wilk S, Bellazzi R. Parimbelli E, et al. Artif Intell Med. 2023 Jan;135:102471. doi: 10.1016/j.artmed.2022.102471. Epub 2022 Dec 1. Artif Intell Med. 2023. PMID: 36628785 - Explainable machine learning models based on multimodal time-series data for the early detection of Parkinson's disease.
Junaid M, Ali S, Eid F, El-Sappagh S, Abuhmed T. Junaid M, et al. Comput Methods Programs Biomed. 2023 Jun;234:107495. doi: 10.1016/j.cmpb.2023.107495. Epub 2023 Mar 23. Comput Methods Programs Biomed. 2023. PMID: 37003039 - The Price of Explainability in Machine Learning Models for 100-Day Readmission Prediction in Heart Failure: Retrospective, Comparative, Machine Learning Study.
Soliman A, Agvall B, Etminani K, Hamed O, Lingman M. Soliman A, et al. J Med Internet Res. 2023 Oct 27;25:e46934. doi: 10.2196/46934. J Med Internet Res. 2023. PMID: 37889530 Free PMC article. - Opening the Black Box: The Promise and Limitations of Explainable Machine Learning in Cardiology.
Petch J, Di S, Nelson W. Petch J, et al. Can J Cardiol. 2022 Feb;38(2):204-213. doi: 10.1016/j.cjca.2021.09.004. Epub 2021 Sep 14. Can J Cardiol. 2022. PMID: 34534619 Review.
Cited by
- A Multimodality Machine Learning Approach to Differentiate Severe and Nonsevere COVID-19: Model Development and Validation.
Chen Y, Ouyang L, Bao FS, Li Q, Han L, Zhang H, Zhu B, Ge Y, Robinson P, Xu M, Liu J, Chen S. Chen Y, et al. J Med Internet Res. 2021 Apr 7;23(4):e23948. doi: 10.2196/23948. J Med Internet Res. 2021. PMID: 33714935 Free PMC article. - Mental health and natural land cover: a global analysis based on random forest with geographical consideration.
Li C, Managi S. Li C, et al. Sci Rep. 2024 Feb 5;14(1):2894. doi: 10.1038/s41598-024-53279-7. Sci Rep. 2024. PMID: 38316893 Free PMC article. - Beyond diagnosis: Leveraging routine blood and urine biomarkers to predict severity and functional outcome in acute ischemic stroke.
Bamodu OA, Chan L, Wu CH, Yu SF, Chung CC. Bamodu OA, et al. Heliyon. 2024 Feb 10;10(4):e26199. doi: 10.1016/j.heliyon.2024.e26199. eCollection 2024 Feb 29. Heliyon. 2024. PMID: 38380044 Free PMC article. - Personalized Prediction of Long-Term Renal Function Prognosis Following Nephrectomy Using Interpretable Machine Learning Algorithms: Case-Control Study.
Xu L, Li C, Gao S, Zhao L, Guan C, Shen X, Zhu Z, Guo C, Zhang L, Yang C, Bu Q, Zhou B, Xu Y. Xu L, et al. JMIR Med Inform. 2024 Sep 20;12:e52837. doi: 10.2196/52837. JMIR Med Inform. 2024. PMID: 39303280 Free PMC article. - Explainable Machine Learning Approach as a Tool to Understand Factors Used to Select the Refractive Surgery Technique on the Expert Level.
Yoo TK, Ryu IH, Choi H, Kim JK, Lee IS, Kim JS, Lee G, Rim TH. Yoo TK, et al. Transl Vis Sci Technol. 2020 Feb 12;9(2):8. doi: 10.1167/tvst.9.2.8. Transl Vis Sci Technol. 2020. PMID: 32704414 Free PMC article.
References
- Kaggle. The State of ML and Data Science 2017 2017. https://www.kaggle.com/surveys/2017.
- Friedman J, Hastie T & Tibshirani R The elements of statistical learning (Springer series in statistics Springer, Berlin, 2001).
- Lundberg SM & Lee S-I in Advances in Neural Information Processing Systems 30 4768–4777 (2017). http://papers.nips.cc/paper/7062-a-unified-approach-to-interpreting-mode....
- Saabas A. treeinterpreter Python package. https://github.com/andosa/treeinterpreter.
- Ribeiro MT, Singh S & Guestrin C Why should i trust you?: Explaining the predictions of any classifier in Proceedings of the 22nd ACM SIGKDD (2016), 1135–1144.
LinkOut - more resources
Full Text Sources
Other Literature Sources