Evolution of altruistic punishments among heterogeneous conditional cooperators - PubMed (original) (raw)
Evolution of altruistic punishments among heterogeneous conditional cooperators
Balaraju Battu. Sci Rep. 2021.
Abstract
It has been known that altruistic punishments solve the free rider problem in public goods games. Considering spatial structure and considering pure strategies significant advances have been made in understanding the evolution of altruistic punishments. However, these models have not considered key behavior regularities observed in experimental and field settings, where the individuals behave like conditional cooperators who are more willing to donate and are also more willing to punish free riders. Considering these behavioral regularities, without imposing a spatial structure on the population, I propose an evolutionary agent-based model in which agents behave like conditional cooperators, each agent's donation conditional on the difference between the number of donations in the past and the threshold value and the propensity value of the agent. Altruistic punishment depends on the difference between the threshold value of the focal agent and the randomly matched another agent. The simulations show that, for certain inflicted costs of punishments, generous altruistic punishments evolve and stabilize cooperation. The results show that, unlike previous models, it is not necessary to punish all free riders equally; it is necessary to do so in the case of the selfish free riders but not in the case of negative reciprocators.
Conflict of interest statement
The author declares no competing interests.
Figures
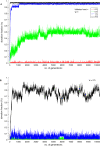
Figure 1
Donation rates for (A) (w) = 1 and for (B) (w) = 0.5 for various cost values for the first 10,000 generations.
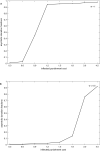
Figure 2
Asymptotic donations, fractions of population with various punishment costs. (A) (w) = 1 and (B) (w) = 0.5.
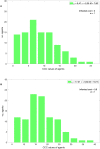
Figure 3
The distribution of CCC values in the 20,000th generation with a bin size of 10. With w = 1 (A) (cost) = 3 and with (B) (cost) = 0.9.
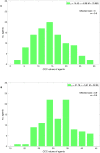
Figure 4
The distribution of CCC values in the 20,000th generation with a bin size of 10. With w = 0.5 (A) (cost) = 3 and with (B) (cost) = 0.9.
Figure 5
Population average β values for various costs in the 20,000th generation. (A) (w) = 1 and (B) (w) = 0.5.
Similar articles
- Cooperation without punishment.
Battu B, Rahwan T. Battu B, et al. Sci Rep. 2023 Jan 21;13(1):1213. doi: 10.1038/s41598-023-28372-y. Sci Rep. 2023. PMID: 36681708 Free PMC article. - Evolution of conditional cooperation in public good games.
Battu B, Srinivasan N. Battu B, et al. R Soc Open Sci. 2020 May 13;7(5):191567. doi: 10.1098/rsos.191567. eCollection 2020 May. R Soc Open Sci. 2020. PMID: 32537191 Free PMC article. - Stable polymorphism of cooperators and punishers in a public goods game.
Oya G, Ohtsuki H. Oya G, et al. J Theor Biol. 2017 Apr 21;419:243-253. doi: 10.1016/j.jtbi.2016.11.012. Epub 2016 Nov 21. J Theor Biol. 2017. PMID: 27880875 - The evolution of strong reciprocity: cooperation in heterogeneous populations.
Bowles S, Gintis H. Bowles S, et al. Theor Popul Biol. 2004 Feb;65(1):17-28. doi: 10.1016/j.tpb.2003.07.001. Theor Popul Biol. 2004. PMID: 14642341 - Evolution of Cooperation with Heterogeneous Conditional Cooperators.
Battu B, Pammi VSC, Srinivasan N. Battu B, et al. Sci Rep. 2018 Mar 14;8(1):4524. doi: 10.1038/s41598-018-22593-2. Sci Rep. 2018. PMID: 29540725 Free PMC article.
Cited by
- Co-evolution of conditional cooperation and social norm.
Battu B. Battu B. Sci Rep. 2023 Oct 3;13(1):16625. doi: 10.1038/s41598-023-43918-w. Sci Rep. 2023. PMID: 37789098 Free PMC article. - Cooperation without punishment.
Battu B, Rahwan T. Battu B, et al. Sci Rep. 2023 Jan 21;13(1):1213. doi: 10.1038/s41598-023-28372-y. Sci Rep. 2023. PMID: 36681708 Free PMC article.
References
- Szolnoki A, Szabó G. Cooperation enhanced by inhomogeneous activity of teaching for evolutionary Prisoner’s Dilemma games. EPL Europhys. Lett. 2007;77:30004. doi: 10.1209/0295-5075/77/30004. - DOI
- Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. doi: 10.1038/359826a0. - DOI
- Szabó G, Fath G. Evolutionary games on graphs. Phys. Rep. 2007;446:97–216. doi: 10.1016/j.physrep.2007.04.004. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous