The load dependence of kinesin's mechanical cycle - PubMed (original) (raw)

The load dependence of kinesin's mechanical cycle

C M Coppin et al. Proc Natl Acad Sci U S A. 1997.

Abstract

Kinesin is a dimeric motor protein that transports organelles in a stepwise manner toward the plus-end of microtubules by converting the energy of ATP hydrolysis into mechanical work. External forces can influence the behavior of kinesin, and force-velocity curves have shown that the motor will slow down and eventually stall under opposing loads of approximately 5 pN. Using an in vitro motility assay in conjunction with a high-resolution optical trapping microscope, we have examined the behavior of individual kinesin molecules under two previously unexplored loading regimes: super-stall loads (>5 pN) and forward (plus-end directed) loads. Whereas some theories of kinesin function predict a reversal of directionality under high loads, we found that kinesin does not walk backwards under loads of up to 13 pN, probably because of an irreversible transition in the mechanical cycle. We also found that this cycle can be significantly accelerated by forward loads under a wide range of ATP concentrations. Finally, we noted an increase in kinesin's rate of dissociation from the microtubule with increasing load, which is consistent with a load dependent partitioning between two recently described kinetic pathways: a coordinated-head pathway (which leads to stepping) and an independent-head pathway (which is static).

PubMed Disclaimer

Figures

Figure 3

Figure 3

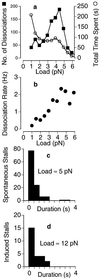
Load dependence of kinesin’s dissociation rate in 40 μM ATP. Kinesin was allowed to take numerous runs (n = 1,050) along the microtubule like the ones shown in Fig. 1. (a) The load at the end point of each run was included in an overall distribution of dissociation loads (▪). The amount of time (number of points) spent under each load was also measured (○). (b) The ratio of these two distributions yields the dissociation rate, which is seen to increase with load up to ≈2/s at ≈5 pN. (c and d) The distribution of stall durations is approximately exponential, with a load-independent mean of 0.57 s (c, ≈5 pN; d, ≈12 pN) corresponding to a dissociation rate of 1.8/s. (Trap stiffness = 0.06 pN/nm.)

Figure 1

Figure 1

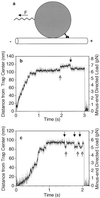
Schematic of the in vitro motility bead assay (not to scale) and examples of displacement data. (a) A single two-headed kinesin molecule adsorbed on the surface of a 1-μm carboxylated latex bead walks toward the plus-end of the microtubule under the opposing (backward) load of an optical trap (F) that acts as a spring. The tether (kinesin tail) between the motor heads and the bead also acts as a spring. The external load can also be directed toward the plus-end of the microtubule to test the behavior of kinesin under a forward load (see Fig. 4). (b and c) Examples of raw data for the bead moving away from the center of the trap against an increasing load. Gray, unfiltered; black, processed with a nonlinear digital moving-average filter (18). Some discrete movements are clearly visible before and during the stall. Balanced back-and-forth movements occur during the stall (arrows), but multiple consecutive backward movements are not seen. When kinesin dissociates the bead falls back into the center of the trap. (Trap stiffness = 0.06 pN/nm; [ATP] = 40 μM.)

Figure 2

Figure 2

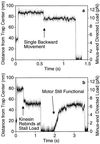
Behavior of kinesin under super-stall loads. While kinesin was moving away from the trap center, the microscope’s piezo stage was abruptly moved by ≈70 nm (at the 50-ms time point in a and b) in the same direction to raise the load to 10–12 pN. (The axoneme and the motor move the same distance as the stage, but the bead only moves ≈60 nm because of the compliance of the motor-bead linkage.) The motor stalls immediately and never walks backwards to the normal stall load of ≈5 pN, although a single backward movement prior to dissociation is common (a). As the bead falls back toward the center of the trap, kinesin can occasionally rebind to the microtubule but only at positions where the load is smaller or equal to the stall load (b). (Trap stiffness = 0.13 pN/nm; [ATP] = 40 μM.)

Figure 4

Figure 4

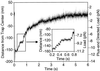
Kinesin-driven movement under forward (plus-end directed) loads. At the 50-ms time point, the piezo stage was abruptly moved ≈200 nm in the direction opposite to that of kinesin movement to place the trap center in front of the motor. The Inset illustrates the observable stepwise character of the movement. The apparent deceleration as the bead approaches the center of the trap, and subsequent apparent long pause, is due to the bead reaching this position in advance of the motor (because of the geometry shown in Fig. 1_a_) and then rotating in place as the motor walks along the microtubule underneath it.

Figure 5

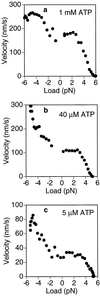
Figure 5

F_–_V curves for kinesin under ATP concentrations of 1 mM (a), 40 μM (b), and 5 μM (c) in a 0.06 pN/nm trap. The right side of each plot (positive loads) pertains to backward loads opposing the movement of the motor. The left side (negative loads) pertains to the forward loading regime derived from experiments like the one shown in Fig. 4. Under a forward load of 5 pN, the motor moves ≈3 times faster than under 0 pN when ATP is rate limiting (b and c), but only about 50% faster under saturating ATP concentrations (1 mM) (a). The F_–_V curve is approximately linear in the 2- to 5-pN range. Approximately 100 runs were used for each curve. The F_–_V curve was obtained for each run individually by running a sliding 300-point linear regression. To control for the effects of biased sampling in calculating the mean at high loads, the runs that did not make it out to high loads were assumed to have zero velocity at those loads (see Materials and Methods). Therefore, the right side of the plots represents a lower bound on the estimate for the true F_–_V curve. Without this correction, the curves would contain slightly more scatter due to runs abruptly dropping out and lie ≈1 pN farther to the right (not shown).

Figure 6

Figure 6

A chemomechanical model of kinesin movement under minus-end directed loads. A simplified cartoon (Upper) depicts an example of an alternating head cycle that is consistent with the proposed kinetic scheme (Lower). In the drawing three adjacent microtubule binding sites are shown. Kinesin moves from left to right toward the plus-end of the microtubule, with its tail tensioned to the left by the laser trap. Black circle, strong binding head; white circle, weak binding head (which may be dissociated or interacting with the binding site); T, ATP; D, ADP; P, phosphate. Some arrows bundle several transitions to simplify the illustration of kinetic partitioning and processivity. The proposed load-dependent transition is represented as a double arrow (⇒), which commits the motor to a net forward movement by allowing the anterior head to adopt a strong binding state (upper pathway). Under high load, this transition is inhibited and the partner head continues its kinetic cycle independently, without achieving a forward step (bent arrow leading to lower pathway). States in which both heads are weakly bound are susceptible to complete dissociation. The rate constants shown in the bottom scheme, where W is weak and S is strong, are those recently reported by Ma and Taylor (10). Several variations on this theme are possible because the chemical intermediates that correspond to the strong and weak states and that are involved in the commitment step (⇒) have not yet been fully defined.

Similar articles

Cited by

References

    1. Vale R D. In: Kinesin. Kreis T, Vale R, editors. Oxford: Oxford Univ. Press; 1993. pp. 199–201.
    1. Svoboda K, Schmidt C F, Schnapp B J, Block S M. Nature (London) 1993;365:721–727. - PubMed
    1. Finer J T, Simmons R M, Spudich J A. Nature (London) 1994;368:113–118. - PubMed
    1. Ishijima A, Harada Y, Kojima H, Funatsu T, Higuchi H, Yanagida T. Biochem Biophys Res Commun. 1994;199:1057–1063. - PubMed
    1. Meyhöfer E, Howard J. Proc Natl Acad Sci USA. 1995;92:574–578. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources