Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na+ channels - PubMed (original) (raw)

Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na+ channels

A Toib et al. J Neurosci. 1998.

Abstract

NaII and NaIIA channels are the most abundant voltage-gated channels in neonatal and adult cortex, respectively. The relationships between activity and availability for activation of these channels were examined using the Xenopus expression system. The main point of this work is that the time constant (tau) of recovery from the unavailable (inactivated) pool is related to the duration (t) of previous activation by a power law: tau(t) = p . tD, with a scaling power D congruent to 0.8 and 0.5 for NaII and NaIIA, respectively, and p as a constant kinetic setpoint. These relationships extend from tens of milliseconds to several minutes and are intrinsic to the channel protein. Coexpression of beta1 auxiliary subunit, together with the alpha subunit of the NaIIA channel, modulates the constant kinetic setpoint but not the scaling power of the latter. The power law scaling between activity and availability is not a universal property of ion channels; unlike that of voltage-gated sodium channels, the rate of recovery from slow inactivation of the ShakerB channel is virtually insensitive to the duration of previous stimuli. It is suggested that the power law scaling described here can act as a molecular memory mechanism that preserves traces of previous activity, over a wide range of time scales, in the form of modulated reaction rates. This mechanism should be considered when theorizing about the dynamics of threshold and firing patterns of neurons.

PubMed Disclaimer

Figures

Fig. 1.

Fig. 1.

Inactivation of voltage-gated sodium channels.A, Time scales of rapid inactivation rates, for both NaII (top) and NaIIA (bottom) channels, are demonstrated using a double-pulse protocol. The membrane is pulsed to −10 mV from a holding potential of −90 mV (pulse duration is 10 msec). The membrane potential of the interval between the first and the second pulses is −90 mV, and its duration is logarithmically increased (note the time axes). The time constants of recovery from rapid inactivation at −90 and −120 mV are summarized in Table 1.B, Representative families of current traces showing the level of slow inactivation are presented. Oocytes are pulsed from a holding potential of −90 to −10 mV for a duration t. After this conditioning depolarization, the oocyte membrane potential is stepped to −120 mV, allowing for recovery from the rapid inactivation process (6 or 100 msec for NaII and NaIIA, respectively; see Materials and Methods, Table 1). The availability of the channels for activation is then tested by an application of a short depolarizing test pulse to −10 mV. The resulting test pulse_current traces_ are shown for both channel subtypes (top, NaII; bottom, NaIIA); note the different time-scale bars (top and_bottom_). The durations (t values) of the conditioning pulses are depicted accordingly. C, Kinetics of entry into the slow inactivation state is shown for NaII (open triangles; n = 6; ±SD) and NaIIA (open diamonds; n = 5; ±SD), together with double exponential functions depicted by_continuous lines_ (NaII, τ1 = 0.6; fraction = 0.33; τ2 = 16.3; fraction = 0.67;R > 0.99; NaIIA, τ1 = 0.6; fraction = 0.31; τ2 = 21.9; fraction = 0.69;R > 0.99). The time course of slow inactivation of NaIIA channels, in response to physiologically realistic stimulation patterns, is depicted by broken lines. In these experiments, during the conditioning phase, the membrane is held at −60 mV and pulsed to 0 mV for 2 msec at various frequencies (filled diamonds, 16 Hz; filled triangles, 45 Hz; filled inverted triangles, 125 Hz; filled circles, 250 Hz). Note that although the main effect of a pulse train is completed within the first 30 sec (i.e., 480 pulses at 16 Hz to 7500 pulses at 250 Hz), accumulation of inactivation continues throughout the examined range (i.e., 1600 pulses at 16 Hz to 25000 pulses at 250 Hz).

Fig. 2.

Fig. 2.

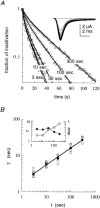
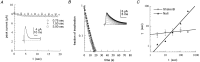
Scaling relationship between the duration of activation and the recovery rate from slow inactivation in voltage-gated sodium channels. A, Time course of recovery from slow inactivation induced by 3-, 10-, 30-, 100-, and 300-sec-long (t) conditioning depolarizations (top, NaII; bottom, NaIIA). The recovery interval, at −90 mV, from the end of the conditioning pulse to the beginning of the series of test pulses lasted 1 sec. The fraction of inactivation was normalized and plotted as described in Materials and Methods. Solid lines are double exponential fits to the data. Insets, Recovery from a 100-sec-long conditioning depolarization from −90 to −10 mV. Recovery from slow inactivation is seen as a gradual increase in peak current responses to test pulses of 15 msec duration from −90 to −10 mV, delivered at a frequency of 0.5 Hz (top) or 0.33 Hz (bottom).B, The value of the slower time constant for recovery from slow inactivation (τ) shown increasing systematically as a function of the duration t of the conditioning depolarization in NaII (n > 6; ±SD) and NaIIA (n = 5; ±SD) channel subtypes. Time constants were extracted from the time course of recovery as shown in_A_, with a test pulse frequency of 0.5 Hz. Solid lines are power law functions of the form τ(t) = p · tD_that were fit to the data (NaII, p = 0.3;D = 0.84; R = 0.99; NaIIA,p = 2.6; D = 0.46;R > 0.99). Inset, The value of the shorter time constant as a function of conditioning depolarization in NaII (open triangles; n > 5; ±SD) and NaIIA (filled diamonds; n > 3; ±SD) channel subtypes. The relative amplitudes of this recovery component (in the absence of the β1 subunit) are within the range of 0.29–0.53 and 0.09–0.33 for NaII and NaIIA, respectively, and do not change systematically as the conditioning-pulse duration is increased.C, Time course of recovery from slow inactivation of NaII channels recorded in detached-macropatch configuration (i.e., the channels are not in contact with intracellular factors). Inactivation was induced by 3-, 10-, 30-, 100-, and 300-sec-long conditioning depolarizations. The recovery interval, at −90 mV, from the end of the conditioning pulse to the beginning of the series of test pulses lasted 1 sec. Solid lines are double exponential fits to the data. Inset, Recovery from a 30 sec conditioning depolarization from −90 to −10 mV. Recovery from slow inactivation is seen as a gradual increase in peak current responses to test pulses of 10 msec duration from −90 to −10 mV, delivered at a frequency of 1 Hz. D, The value of the slower time constant (τ) increasing systematically as a function of t. Mean values (filled circles) are fitted with a power law of the form: τ(t) = p ·_tD (p = 0.7; D = 0.75; R = 0.97).

Fig. 3.

Fig. 3.

Effect of the β1 subunit on the entry of NaIIA to slow inactivation. A, Typical responses of NaIIA(α) and NaIIA(α + β1) channels to a depolarization pulse from −90 to −10 mV. These traces were recorded from different oocytes (of the same batch) 3 d after injection with cRNA of the α subunit alone (dashed line) or together with cRNA of the β1 subunit (continuous line) in a ≅1:1 molar ratio. The presence of β1 subunit results in a faster activation and inactivation kinetics. No systematic effect on current amplitude was observed. B, A representative family of current responses to test pulses from −120 to −10 mV, delivered 100 msec after the end of a t long conditioning depolarization to −10 mV, showing the level of slow inactivation of NaIIA(α + β1) channels. C, Kinetics of entry into the slow inactivation state for NaIIA(α + β1) channels (open symbols). For comparison, two types of exponential functions are fitted to the mean values (filled symbols), a single exponent (τ = 4.8 sec; R = 0.92) and a double exponent (τ1 = 2.12; fraction = 0.55; τ2 = 24.3; fraction = 0.45; R > 0.99).

Fig. 4.

Fig. 4.

Scaling relationship between the duration of activation and recovery rate from slow inactivation in NaIIA channels that are coexpressed with the β1 subunit. A, Time course of recovery from slow inactivation in NaIIA(α + β1) channels induced by 3-, 10-, 30-, 100-, and 300-sec-long (t) conditioning depolarizations. The recovery interval, at −90 mV, from the end of the conditioning pulse to the beginning of the series of test pulses lasted 1 sec. The fraction of inactivation was normalized and plotted as described in Materials and Methods. Solid lines are double exponential fits to the data.Inset, Recovery from a 100 sec conditioning depolarization. Recovery from slow inactivation is seen as a gradual increase in peak current responses to test pulses from −90 to −10 mV, delivered at a frequency of 0.5 Hz. B, The value of the slower time constant (τ) increasing systematically as a function of_t_. Time constants were extracted from the time course of recovery as shown in A, with a test pulse frequency of 0.5 Hz. Filled circles are the mean values at each t. The solid line is a power law function of the form τ(t) = p · tD that was fit to the mean values (p = 1.88; D = 0.45;R > 0.99). Inset, The relative amplitude (filled diamonds, right_y_-axis) and time constant (open circles, left _y_-axis) of the faster component of recovery from slow inactivation, for the cell shown in A, as a function of conditioning-pulse duration.

Fig. 5.

Fig. 5.

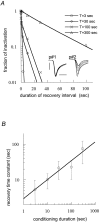
Scaling relationship between the conditioning duration and recovery time course in long double-pulse protocols with NaIIA(α + β1) channels. A, Exemplar recovery time courses that were extracted from double-pulse protocols as follows: A short test pulse was applied 1 sec before each conditioning pulse. This short test pulse (p#1 in the_inset_) served as a control level for the calculation of inactivation fraction (see Materials and Methods) and as a measure for full recovery between pairs of pulses. Each T_-sec-long conditioning pulse was followed by a recovery interval at −90 mV and a single test pulse to −10 mV (p#2 in the_inset). This procedure was repeated for various recovery intervals and conditioning durations. Insets, Control and recovery pulse pairs for 300 sec conditioning duration. Calibration: 4 msec, 4 μA. B, Relationship between conditioning duration and recovery time constant fitted to a power law function of the form: τ(t) = p · tD (p = 2.9;D = 0.52; R = 0.96). Means and SDs of recovery time constants are from three oocytes.

Fig. 6.

Fig. 6.

Scaling relationship between the conditioning duration and recovery time course that persists over a range of recovery voltages. A, Exemplar recovery time courses at three recovery voltages (−60, −90, and −120 mV) are shown. The membrane is stepped to a −10 mV conditioning voltage for a duration_t_ (10, 100, or 300 sec). Recovery was measured by applying a series of test pulses to −10 mV and was normalized and plotted as described in Materials and Methods. Note that at all three recovery voltages, the time course of recovery becomes slower as the duration of the conditioning pulse is increased. At −60 mV compared with the other two voltages, the recovery time course seems to be more sensitive to the duration of the conditioning pulse. B, This becomes evident in this figure, where the value of the slower time constant (τ) is plotted as a function of the conditioning duration_t_. The slower time constants were extracted from the time course of recovery as shown in A. Filled circles are the mean values at −120 mV; open circles are the mean values at −60 mV. The scaling powers are 0.6 (R > 0.97) and 0.4 (R > 0.99) for −60 and −120 mV, respectively.

Fig. 7.

Fig. 7.

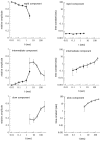
The relationships between different components of recovery from inactivation. The relative amplitudes and time constants of the rapid (top), intermediate (middle), and slow (bottom) recovery components are shown. Filled circles depict results of a double-pulse procedure; open circles depict results of a pulse-series procedure (see Pulse protocols and analysis of slow recovery in voltage-gated sodium channels in Materials and Methods). During long conditioning pulses (>3 sec), the oocytes were kept under continuous perfusion at a rate of ∼2–4 ml/min, a critical factor when a kinetic analysis of the intermediate component of recovery is sought (see Electrophysiological measurements in Materials and Methods). Note the dynamics of the relative amplitudes as the conditioning duration t is increased. Also note that unlike that of the intermediate and slow components, the time constant of the rapid component is insensitive to the duration of the conditioning pulse.

Fig. 8.

Fig. 8.

ShakerB channels recover from slow inactivation in a uniquely defined time scale. A, Evaluation of the duration of interpulse interval (at −90 mV) that is required for avoidance of accumulation of inactivation because of 50-msec-long depolarizing test pulses to +40 mV is shown. These pulse parameters (amplitude and duration) allow for a completion of the N-type inactivation process. Slight accumulation of inactivation (saturating at ≅5%) appears when pulses are delivered once every 750 msec (open circles). Intervals of 1.5 sec (open diamonds) and 3 sec (open squares) allow for complete recovery between test pulses. Inset, Fourteen superposed current responses to identical 50-msec-long depolarizing voltage pulses from −90 to +40 mV separated by 1.5 sec intervals at −90 mV are shown. B, ShakerB channels demonstrate a uniquely defined time scale for recovery from slow (C-type) inactivation. Slow inactivation was induced by conditioning depolarizations to 0 mV from a holding potential of −90 mV. The recovery interval, at −90 mV, from the end of the conditioning pulse to the beginning of the series of test pulses lasted 1 sec. The fraction of inactivation was normalized and plotted as described in Materials and Methods, taking into account the positive sign of the currents. This time scale (≅5 sec) is independent of the duration_t_ of the conditioning depolarization (open circles, t = 3 sec; open squares, t = 10 sec; open diamonds, t = 30 sec; X,t = 100 sec; and plus signs,t = 300 sec). Inset, Recovery from a 100 sec conditioning depolarization to 0 mV is shown. Recovery from slow inactivation is seen as a gradual increase in peak current responses to 20-msec-long test pulses from −90 to 0 mV, which were delivered once per second. C, Comparison of the relationship between the duration of depolarization and the rate of recovery from slow inactivation of NaII (filled triangles, mean values from Fig. 2_B_) and ShakerB (open circles, n > 3; ±SD) is shown. Solid lines are power law functions of the form τ(t) = p · tD that were fit to the mean values (NaII,p = 0.3; D = 0.84;R = 0.99; ShakerB, p = 3.7;D = 0.09; R > 0.99).

Fig. 9.

Fig. 9.

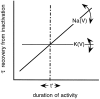
The nature of interaction between slow inactivation of voltage-gated sodium [Na(V)] and potassium [K(V)] channels: an inference. A scheme of behavior for voltage-gated sodium and potassium channels. The position of the point of intersection (dashed line) and the relative_slopes_ of the functions are variables that reflect the composition of ion channels that is unique to a neuron at a given point of time. It is suggested that these variables are dynamic (_two_-headed arrows) and influenced by the developmental stage and by activity.

Similar articles

Cited by

References

    1. Adelman WJ, Palti Y. The effects of external potassium and long duration voltage conditioning on the amplitude of sodium currents in the giant axon of the squid, Loligo peali. J Gen Physiol. 1969;54:589–606. - PMC - PubMed
    1. Almers W, Stanfield PR, Stühmer W. Slow changes in currents through sodium channels in frog muscle membrane. J Physiol (Lond) 1983;339:253–271. - PMC - PubMed
    1. Auld VJ, Goldin AL, Krafte DS, Marshall J, Dunn JM, Catterall WA, Lester HA, Davidson N, Dunn RJ. A rat brain Na+ channel alpha subunit with novel gating properties. Neuron. 1988;1:449–461. - PubMed
    1. Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal physiology. Oxford UP; New York: 1994.
    1. Brismar T. Slow mechanism for sodium permeability inactivation in myelinated nerve fibre of Xenopus laevis. J Physiol (Lond) 1977;270:283–297. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources