Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses - PubMed (original) (raw)

Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses

R A Silver et al. J Physiol. 1998.

Abstract

1. EPSCs were recorded under whole-cell voltage clamp at room temperature from Purkinje cells in slices of cerebellum from 12- to 14-day-old rats. EPSCs from individual climbing fibre (CF) inputs were identified on the basis of their large size, paired-pulse depression and all-or-none appearance in response to a graded stimulus. 2. Synaptic transmission was investigated over a wide range of experimentally imposed release probabilities by analysing fluctuations in the peak of the EPSC. Release probability was manipulated by altering the extracellular [Ca2+] and [Mg2+]. Quantal parameters were estimated from plots of coefficient of variation (CV) or variance against mean conductance by fitting a multinomial model that incorporated both spatial variation in quantal size and non-uniform release probability. This 'multiple-probability fluctuation' (MPF) analysis gave an estimate of 510 +/- 50 for the number of functional release sites (N) and a quantal size (q) of 0.5 +/- 0.03 nS (n = 6). 3. Control experiments, and simulations examining the effects of non-uniform release probability, indicate that MPF analysis provides a reliable estimate of quantal parameters. Direct measurement of quantal amplitudes in the presence of 5 mM Sr2+, which gave asynchronous release, yielded distributions with a mean quantal size of 0.55 +/- 0.01 nS and a CV of 0.37 +/- 0.01 (n = 4). Similar estimates of q were obtained in 2 mM Ca2+ when release probability was lowered with the calcium channel blocker Cd2+. The non-NMDA receptor antagonist 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; 1 microM) reduced both the evoked current and the quantal size (estimated with MPF analysis) to a similar degree, but did not affect the estimate of N. 4. We used MPF analysis to identify those quantal parameters that change during frequency-dependent depression at climbing fibre-Purkinje cell synaptic connections. At low stimulation frequencies, the mean release probability (pr) was unusually high (0.90 +/- 0.03 at 0.033 Hz, n = 5), but as the frequency of stimulation was increased, pr fell dramatically (0.02 +/- 0.01 at 10 Hz, n = 4) with no apparent change in either q or N. This indicates that the observed 50-fold depression in EPSC amplitude is presynaptic in origin. 5. Presynaptic frequency-dependent depression was investigated with double-pulse and multiple-pulse protocols. EPSC recovery, following simultaneous release at practically all sites, was slow, being well fitted by the sum of two exponential functions (time constants of 0.35 +/- 0.09 and 3.2 +/- 0.4 s, n = 5). EPSC recovery following sustained stimulation was even slower. We propose that presynaptic depression at CF synapses reflects a slow recovery of release probability following release of each quantum of transmitter. 6. The large number of functional release sites, relatively large quantal size, and unusual dynamics of transmitter release at the CF synapse appear specialized to ensure highly reliable olivocerebellar transmission at low frequencies but to limit transmission at higher frequencies.

PubMed Disclaimer

Figures

Figure 1

Figure 1. Identification and optimization of CF EPSC recordings

A, CF EPSCs identified on the basis of paired-pulse depression. Part of the stimulus artifact was omitted for clarity. B, EPSC and failure evoked at just above and just below the stimulation threshold and recorded at high gain to check that no parallel fibre responses were present. C, stimulus-response relationship for climbing fibre EPSCs recorded at 0.2 Hz (excluding failures). The slight relaxation just above threshold is due to the effect of failures around the stimulation threshold and frequency-dependent depression of the synaptic current. Error bars were smaller than symbol size and therefore omitted. D, leak-subtracted voltage-activated currents in a Purkinje cell held at -30 and -60 mV. Depolarizations indicated at the top were incremented by 5 mV. E, simultaneous current and voltage recording at the Purkinje cell soma during CF activation. F, correction of EPSC for escape voltage across the electrode. Correction 1 was done using recorded voltage from E, and correction 2 was done using the voltage escape calculated from compensated electrode resistance. Dashed lines in E and F show baseline level before CF activation.

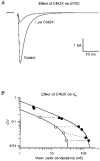
Figure 6

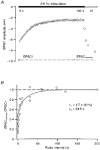
Figure 6. Testing the MPF analysis method

A, averaged EPSCs recorded in control solution (2 m

m

Ca2+, 1 m

m

Mg2+ at 0.2 Hz) and in the presence of 1 μ

m

CNQX. Stimulus artifact omitted for clarity. B, relationship between CV and synaptic conductance measured from EPSCs recorded at different frequencies (0.033-10 Hz) in control solution (•) and in the presence of 1 μ

m

CNQX (^). The dotted lines indicate measurements made at the same frequency. In the presence of CNQX the synaptic conductance was reduced but the CV remained similar. The continuous lines show the compound multinomial fit to the two data sets. The quantal size, estimated from the fit, was substantially reduced in CNQX, but the number of release sites was similar to control.

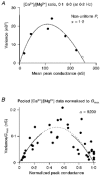
Figure 5

Figure 5. Individual and pooled variance-conductance plots

A, measured variance-mean synaptic conductance plot from a CF input that showed non-uniformity in _P_r. •, recorded at 0.2 Hz; ^, recorded at 0.033 Hz. The continuous line shows the fit to the compound multinomial model (eqn (9)) with _q_m = 0.40 and _N_m = 639. If the underlying _P_r distribution approximates a family of beta distributions, CV _P_r can be calculated from α using eqn (5) (see Methods). B, pooled variance-conductance relationship normalized by peak conductance. •, pooled data from six cells where data from each cell were normalized by the maximal conductance (_G_max), so the abscissa is approximately equal to _P_¯r. The dotted line shows the fit using eqn (10) (_q_m = 0.47). The continuous lines show a fit for the simple multinomial model over the low _P_¯r range (_P_¯r = 0-0.3, _q_m = 0.46) and the high _P_¯r range (_P_¯r = 0.7-1.0, _q_m = 0.44). The similarity in the quantal estimates from the different _P_¯r regions, and the high α value obtained with the compound multinomial fit, indicates that there was no systematic distortion of the variance-conductance relationship by non-uniform _P_r at the CF synaptic connection.

Figure 2

Figure 2. Estimating quantal parameters with MPF analysis

A, superimposed EPSCs (6 shown) recorded at 0.2 Hz stimulation in different [Ca2+]/[Mg2+] solutions. Holding voltage, -30 mV. B, relationship between CV and mean synaptic conductance at the peak of the EPSC for the cell in A. •, measurements made at different release probabilities, set by the [Ca2+]/[Mg2+] ratio at 0.2 Hz. ^, measurement recorded at 0.033 Hz. The continuous line is a simple binomial fit to the data (eqn (1)). C, relationship between variance and mean synaptic conductance at the peak of the EPSC (same cell as A and B). Continuous line shows the fit with a binomial relationship (eqn (2)), which gave _N_b = 285 and _q_b = 0.61 nS for this cell.

Figure 3

Figure 3. Variation in quantal size

A, evoked EPSCs recorded at 0.2 Hz in 5 m

m

Sr2+, 1 m

m

Mg2+ at -70 mV. The peak of the EPSC was cropped to illustrate asynchronous quantal events in the tail. Inset shows later EPSCs with initial part of current omitted. Bar indicates analysis window. B, amplitude histogram of 401 asynchronous quantal events from the cell shown in A, yielding a mean quantal size, q, of 0.56 nS and a CV of 0.39. ▪, background noise.

Figure 4

Figure 4. Effect of non-uniform release probability on MPF analysis

A, examples of beta distributions used to model the distribution of _P_r. Continuous lines show three representative examples of distributions with α = 1 and _P_¯r as specified on the graph (in parentheses). Dashed line shows a single example of a beta distribution from the set generated with α = 5. B, relationship between the coefficient of variation of _P_r (CV _P_r) and _P_¯r for sets of beta distributions with α = 0.1, α = 1 and α = 5. Each curve was generated by calculating CV _P_r (eqn (5)) for 100 beta distributions where α was constant and _P_¯r = α/(α+β). •, values for the three α = 1 distributions and one α = 5 distribution shown as examples in A. C, relationship between predicted EPSC variance and _P_¯r, for uniform and non-uniform _P_r cases. All plots were calculated assuming N = 600 and q = 0.44 nS using eqn (6). Dotted line indicates the case for uniform _P_r (where CV _P_r = 0). Continuous lines show the non-uniform _P_r cases where CV _P_r was calculated as a function of _P_¯r using eqn (6) with α = 0.1, α = 1 and α = 5 (as shown in B). D, simulated negative correlations between quantal size and release probability at each site. Examples of relationships between _P_r and q for a simulated synapse with 100 release sites at four different mean release probabilities values (shown in parentheses). The _P_r was calculated from cumulative beta distributions (α = 1) and q was derived from measured quantal amplitudes recorded in Sr2+ (see Methods). The mean and CV of q were 0.653 nS and 0.426, respectively. The negative correlation was generated by positively ranking _P_r and negatively ranking q with site number. E, normalized variance-mean release probability relationships for simulated synapses with correlations between _P_r and q. ^, negative correlation between _P_r and q for the same simulation as D. •, corresponding positive correlation between _P_r and q. Continuous line shows theoretical relationship for the same case when _P_r and q are not correlated. Dotted line shows the theoretical relationship for the same non-uniform q when _P_r is uniform. Results of fits of the compound multinomial model to correlated data are shown in Table 1.

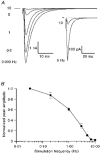
Figure 7

Figure 7. Frequency-dependent depression of the CF EPSC

A, averaged EPSCs from the same input recorded at different simulation frequencies. Inset shows the same 5 and 10 Hz data at a higher gain. Mean currents were collected once EPSC amplitude had reached steady state. Part of the stimulus artifact was omitted for clarity. B, frequency dependence of EPSC peak amplitude. EPSC amplitude was normalized to the peak amplitude at 0.033 Hz. For all points, n = 5 (except 10 Hz, n = 4).

Figure 8

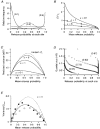
Figure 8. Quantal parameters during frequency-dependent depression

A, mean EPSC waveforms recorded at 0.2 and 3 Hz in 2 m

m

Ca2+, 1 m

m

Mg2+ at -30 mV. B, relationship between CV and mean synaptic conductance for 3 Hz stimulation. C, relationship between variance and mean synaptic conductance for 3 Hz stimulation. Data in A, B and C are from the same cell as shown in Fig. 2. In B and C, each data point shows a measurement made at a different release probability set with a particular [Ca2+]/[Mg2+] solution, and the continuous lines are the binomial relationships derived from data in Fig. 2 (a compound multinomial fit to these data gave a relationship with a similar shape, α = 10.7). The fact that the 3 Hz data fall on the same binomial relationship indicates that the EPSC depression was caused by a reduction in release probability rather than a change in N or q.

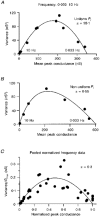
Figure 9

Figure 9. Variance-conductance plots generated by changing stimulation frequency

A, relationship between variance and synaptic conductance at the peak of the EPSC recorded at different frequencies in 2 m

m

Ca2+, 1 m

m

Mg2+. Continuous line shows the compound multinomial fit. The large α value indicates that _P_r is relatively uniform at this synapse. B, a variance-conductance plot from a cell that showed significant dispersion in _P_r. Note the skewed shape of the plot and the low α value of the fitted compound multinomial function (eqn (9)). C, pooled normalized variance-conductance relationship obtained at different stimulation frequencies. Symbols show data from five CF inputs where data from each cell were normalized by the maximal conductance (_G_max), so the abscissa is approximately equal to _P_¯r. The continuous line shows the compound multinomial fit using eqn (10) (_q_m = 0.71). The α value of the fit to this pooled data indicates a relatively small systematic distortion by non-uniform _P_r.

Figure 10

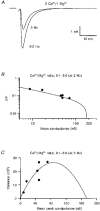
Figure 10. Recovery of _P_¯r following transmitter release

A, relationship between release probability and stimulation frequency calculated from the relationship in Fig. 7_B_. B, seven superimposed trials from a paired-pulse experiment with stimulus artifacts removed for clarity. The intertrial period was 30 s, so the first EPSC of the pair (EPSC1) had a high release probability (_P_¯r, ∼0.90). The dashed line indicates the full recovery amplitude. C, EPSC recovery plot for the same cell as shown in B. This was constructed by plotting the ratio of the paired EPSC amplitudes against the paired-pulse interval. Each data point indicates the results from an individual paired-pulse trial, except the 30 s point, which was normalized to one. The continuous line shows the fit to the sum of two exponentials. Since the depression is presynaptic, this represents the time course of recovery of _P_¯r following release at almost all sites.

Figure 11

Figure 11. Onset of and recovery from depression of _P_¯r with sustained transmitter release

A, onset and recovery of EPSC amplitude with sustained stimulation. Filled bar indicates duration of stimulation at 2.8 Hz; open bar indicates variable interpulse interval. Small open circles indicate onset time course of depression after first EPSC (mean of 4 trials); large open circles show EPSC1 and last EPSC (each point a single trial; EPSCrecovery). Each trial was separated by an interval of 200 s to ensure full recovery of _P_¯r. Dashed line shows amplitude of EPSC1 and thus the full recovery amplitude. B, recovery time course data for five cells. Time course was constructed by plotting the ratio of EPSCrecovery and EPSC1 against the interval between the last EPSC in the 2.8 Hz train and EPSCrecovery. The continuous line shows the fit to the sum of two exponential functions. Since the depression is presynaptic at this frequency, the time course represents the recovery of _P_¯r following sustained release.

Similar articles

Cited by

References

    1. Abdul-Ghani MA, Valiante TA, Pennefather PS. Sr2+ and quantal events at excitatory synapses between mouse hippocampal neurons in culture. Journal of Physiology. 1996;495:113–125. - PMC - PubMed
    1. Altman J. Postnatal development of the cerebellar cortex in the rat. II. Phases in the maturation of Purkinje cells and of the molecular layer. Journal of Comparative Neurology. 1972;145:399–463. - PubMed
    1. Armstrong DM, Rawson JA. Activity patterns of cerebellar cortical neurones and climbing fibre afferents in the awake cat. Journal of Physiology. 1979;289:425–448. - PMC - PubMed
    1. Barbour B, Häusser M. Intersynaptic diffusion of neurotransmitter. Trends in Neurosciences. 1997;20:377–384. <10.1016/S0166-2236%2896%2920050-5>. - DOI - PubMed
    1. Barnes-Davies M, Forsythe ID. Pre- and postsynaptic glutamate receptors at a giant excitatory synapse in rat auditory brainstem slices. Journal of Physiology. 1995;488:387–406. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources