Conformation gating as a mechanism for enzyme specificity - PubMed (original) (raw)
Conformation gating as a mechanism for enzyme specificity
H X Zhou et al. Proc Natl Acad Sci U S A. 1998.
Abstract
Acetylcholinesterase, with an active site located at the bottom of a narrow and deep gorge, provides a striking example of enzymes with buried active sites. Recent molecular dynamics simulations showed that reorientation of five aromatic rings leads to rapid opening and closing of the gate to the active site. In the present study the molecular dynamics trajectory is used to quantitatively analyze the effect of the gate on the substrate binding rate constant. For a 2. 4-A probe modeling acetylcholine, the gate is open only 2.4% of the time, but the quantitative analysis reveals that the substrate binding rate is slowed by merely a factor of 2. We rationalize this result by noting that the substrate, by virtue of Brownian motion, will make repeated attempts to enter the gate each time it is near the gate. If the gate is rapidly switching between the open and closed states, one of these attempts will coincide with an open state, and then the substrate succeeds in entering the gate. However, there is a limit on the extent to which rapid gating dynamics can compensate for the small equilibrium probability of the open state. Thus the gate is effective in reducing the binding rate for a ligand 0.4 A bulkier by three orders of magnitude. This relationship suggests a mechanism for achieving enzyme specificity without sacrificing efficiency.
Figures
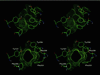
Figure 1
Opening and closing of the gate to the active site of AChE. The five aromatic residues serving as the gate are shown such that the viewer is looking down the active-site gorge and into the active site. The surface accessible to a 1.4-Å probe is shown as dots. (Upper) Configuration at 12 ps along a 750-ps MD trajectory. The gate is closed to the 1.4-Å probe (but is open to a 1.2-Å probe). (Lower) Configuration at 68 ps along the MD trajectory. The gate is open even to a 2.6-Å probe (but is closed for a 2.8-Å probe).
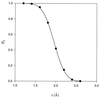
Figure 2
Equilibrium probability _p_o that the gate opens wide enough to admit a substrate with size s. Each circle represents the fraction of time the half-width x of the gate is larger than a particular value of s, calculated from the 750-ps MD trajectory. The curve is a fit assuming that x has a Gaussian distribution.
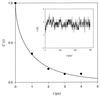
Figure 3
Number correlation function for the transition of the gate half-width x between x < _s_ = 2.4 Å and _x_ > s. Circles are calculated from the 750-ps MD trajectory as 〈{_H_[x(t) − _s_] − _p_o]}{_H_[x(0) − _s_] − _p_o]}〉/〈{_H_[x(0) − _s_] − _p_o]}2〉 (ref. 15), where H(x) is the step function. The curve is a fit to Eq. 4, which is calculated for diffusion in a harmonic potential. (Inset) Fluctuations of the gate half-width along the 750-ps MD trajectory.
References
- Nolte H-J, Rosenberry T L, Neumann E. Biochemistry. 1980;19:3705–3711. - PubMed
- Pryor A N, Selwood T, Leu L-S, Andracki M A, Lee B H, Rao M, Rosenberry R, Doctor B P, Silman I, Quinn D M. J Am Chem Soc. 1992;114:3896–3900.
- Radic Z, Gibney G, Kawamoto S, MacPhee-Quigley K, Bongiorno C, Taylor P. Biochemistry. 1992;31:9760–9767. - PubMed
- Fersht A. Enzyme Structure and Mechanism. 2nd Ed. New York: Freeman; 1985. pp. 150–154.
- Sussman J L, Harel M, Frolow F, Oefner C, Goldman A, Toker L, Silman I. Science. 1991;253:872–879. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources