LayerNorm — PyTorch 2.7 documentation (original) (raw)

class torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, bias=True, device=None, dtype=None)[source][source]¶

Applies Layer Normalization over a mini-batch of inputs.

This layer implements the operation as described in the paper Layer Normalization

y=x−E[x]Var[x]+ϵ∗γ+βy = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta

The mean and standard-deviation are calculated over the last D dimensions, where Dis the dimension of normalized_shape. For example, if normalized_shapeis (3, 5) (a 2-dimensional shape), the mean and standard-deviation are computed over the last 2 dimensions of the input (i.e. input.mean((-2, -1))).γ\gamma and β\beta are learnable affine transform parameters ofnormalized_shape if elementwise_affine is True. The variance is calculated via the biased estimator, equivalent totorch.var(input, unbiased=False).

Note

Unlike Batch Normalization and Instance Normalization, which applies scalar scale and bias for each entire channel/plane with theaffine option, Layer Normalization applies per-element scale and bias with elementwise_affine.

This layer uses statistics computed from input data in both training and evaluation modes.

Parameters

• normalized_shape (int or list or torch.Size) –
  input shape from an expected input of size
  [∗×normalized_shape[0]×normalized_shape[1]×…×normalized_shape[−1]][* \times \text{normalized\_shape}[0] \times \text{normalized\_shape}[1] \times \ldots \times \text{normalized\_shape}[-1]]
  If a single integer is used, it is treated as a singleton list, and this module will normalize over the last dimension which is expected to be of that specific size.
• eps (float) – a value added to the denominator for numerical stability. Default: 1e-5
• elementwise_affine (bool) – a boolean value that when set to True, this module has learnable per-element affine parameters initialized to ones (for weights) and zeros (for biases). Default: True.
• bias (bool) – If set to False, the layer will not learn an additive bias (only relevant ifelementwise_affine is True). Default: True.

Variables

• weight – the learnable weights of the module of shapenormalized_shape\text{normalized\_shape} when elementwise_affine is set to True. The values are initialized to 1.
• bias – the learnable bias of the module of shapenormalized_shape\text{normalized\_shape} when elementwise_affine is set to True. The values are initialized to 0.

Shape:

• Input: (N,∗)(N, *)
• Output: (N,∗)(N, *) (same shape as input)

Examples:

NLP Example

batch, sentence_length, embedding_dim = 20, 5, 10 embedding = torch.randn(batch, sentence_length, embedding_dim) layer_norm = nn.LayerNorm(embedding_dim)

Activate module

layer_norm(embedding)

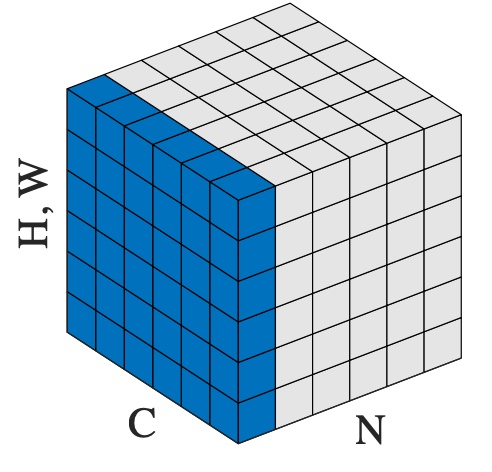
Image Example

N, C, H, W = 20, 5, 10, 10 input = torch.randn(N, C, H, W)

Normalize over the last three dimensions (i.e. the channel and spatial dimensions)

as shown in the image below

layer_norm = nn.LayerNorm([C, H, W]) output = layer_norm(input)