HeavisidePi—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • HeavisideTheta
  • DiracDelta
  • HeavisideLambda
  • UnitBox
• Related Guides
  • Generalized Functions
  • Integral Transforms

HeavisidePi

HeavisidePi[x]

represents the box distribution 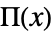, equal to 1 for 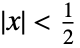and 0 for .

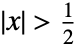HeavisidePi[x1,x2,…]

represents the multidimensional box distribution 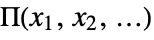which is 1 if all .

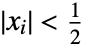Examples

open allclose all

Basic Examples (4)

Evaluate numerically:

Plot in one dimension:

Plot in two dimensions:

The derivative generates DiracDelta distributions:

Scope (38)

Numerical Evaluation (6)

Evaluate numerically:

HeavisidePi always returns an exact result:

Evaluate efficiently at high precision:

HeavisidePi threads over lists:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix HeavisidePi function using MatrixFunction:

Specific Values (4)

Value at zero:

As a distribution, HeavisidePi does not have specific values at :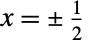

Evaluate symbolically:

Find a value of x for which the HeavisidePi[x]=1:

Visualization (4)

Function Properties (12)

Differentiation (4)

Differentiate the univariate HeavisidePi:

Differentiate the multivariate HeavisidePi:

Higher derivatives with respect to z:

Differentiate a composition involving HeavisidePi:

Integration (4)

Integrate over finite domains:

Integrate over infinite domains:

Numerical integration:

Integrate expressions containing symbolic derivatives of HeavisidePi:

Integral Transforms (4)

Applications (2)

Integrate a function involving HeavisidePi symbolically and numerically:

Solve an initial value problem for the heat equation:

Specify an initial value:

Solve the initial value problem using :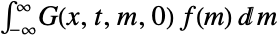

Compare with the solution given by DSolveValue:

Properties & Relations (2)

Wolfram Research (2008), HeavisidePi, Wolfram Language function, https://reference.wolfram.com/language/ref/HeavisidePi.html.

Text

Wolfram Research (2008), HeavisidePi, Wolfram Language function, https://reference.wolfram.com/language/ref/HeavisidePi.html.

CMS

Wolfram Language. 2008. "HeavisidePi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeavisidePi.html.

APA

Wolfram Language. (2008). HeavisidePi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeavisidePi.html

BibTeX

@misc{reference.wolfram_2025_heavisidepi, author="Wolfram Research", title="{HeavisidePi}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/HeavisidePi.html}", note=[Accessed: 10-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_heavisidepi, organization={Wolfram Research}, title={HeavisidePi}, year={2008}, url={https://reference.wolfram.com/language/ref/HeavisidePi.html}, note=[Accessed: 10-June-2025 ]}