tallsystem – Store norske leksikon (original) (raw)
Tallsystem er et system for å skrive tall og for å telle. Det finnes mange ulike systemer for telling og tallrepresentasjon som har vært brukt gjennom historien.
Vårt vanlige tallsystem kalles titallsystemet, og er et posisjonssystem med 10 som grunntall. To-tallsystemet er et annet posisjonssystem, mens romertall er et addisjonssystem.
To-tallsystemet brukes i datamaskiner.
Addisjonssystemer

Den aller enkleste måten å angi tall ved symboler er å representere tallet 1 med ett merke (for eksempel en strek), tallet 2 med to merker og så videre. Tallene får raskt en lengde som er vanskelig å få oversikt over, men man kan da skrive merkene i grupper på en fast størrelse – vanligvis fem eller ti – for å lette opptellingen. Dette gjør mange ofte fortsatt når man ved opptelling setter hver femte strek på skrå over de fire foregående. Det neste skrittet i utviklingen er å skrive et eget symbol for 5, og overgangen til egne symboler for 10, 20 og så videre er da enkel.
Felles for disse systemene er at det tallet som skal representeres fremkommer ved at man legger sammen (adderer) verdien til alle symbolene som brukes, uavhengig av rekkefølgen. Slike systemer kalles derfor addisjonssystemer.
En variant får man ved å innføre regelen om at et mindre tall til høyre for et større skal legges til, mens et mindre tall til venstre for et større skal trekkes fra. Dette systemet ble brukt av romerne (se romertall), slik at VI betyr 6, mens IV betyr 4. I dette tilfellet er ikke rekkefølgen vilkårlig.
En videreutvikling av addisjonssystemet er å innføre ekstra tegn som angir at et talltegn skal ganges (multipliseres) med en bestemt faktor, vanligvis 10. Addisjonssystemer som bruker dette multiplikasjonsprinsippet kalles hybride systemer.
Posisjonssystemer
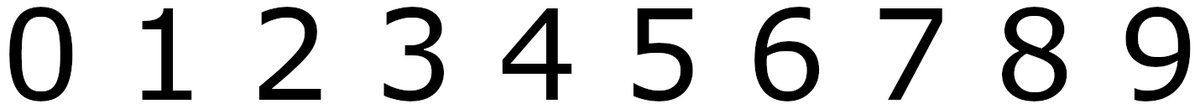
Talltegnene fra 0 til 9, som vi bruker i titallssystemet, kalles arabiske tall
I et posisjonssystem representerer hvert talltegn et multiplum av et bestemt tall (grunntallet), avhengig av hvor det står. Det mest utbredte posisjonssystemet er vårt titallsystem (det dekadiske tallsystemet). Tallene vi bruker er symboler for tallene 0 til 9, og hvert symbol representerer et multiplum av en potens av 10 avhengig av posisjon eller plassering. Tallet 10 er altså grunntallet.
Tallet som skrives 7452 i titallsystemet står for eksempel for
\[7 \times 10^3 + 4 \times 10^2 + 5 \times 10^1 + 2 \times 10^0\]
altså 7000 + 400 + 50 + 2.
I tall med desimaler representerer det første tallet etter komma tideler, det andre hundredeler og så videre. Tallet 0,382 står derfor for
\[3 \times 10^{-1} + 8 \times 10^{-2} + 2 \times 10^{-3}\]
Posisjonssystemet har en rekke fordeler når det gjelder kompakthet og mulighet til å fremstille komplisert matematikk, og det har ingen begrensning når det gjelder hvor store tall som kan uttrykkes.
Oppfinnelsen av et tegn for null, som er nødvendig i et posisjonssystem, regnes som en av de største matematiske oppfinnelser noensinne. Null ble innført i babylonsk matematikk omkring 300-tallet fvt., og vi regner vanligvis med at babylonerne fikk ideen fra India.
Andre grunntall som har vært i bruk er 5, 10, 12, 20 og 60. Rester av det babylonske sekstitallsystemet finner vi fortsatt i inndelingen av timer, minutter og vinkler i 60. I tolvtallsystemet vil tallet 7452 bety 7 × 123 + 4 × 122 + 5 × 121 + 2 × 120, som tilsvarer 12 734 i titallsystemet.