Home Page - Metamath (original) (raw)

Mirror Site Selection	Metamath Home Page	This page:FAQ Downloads Download help Reviews

Metamath is a simple and flexible computer-processable language that supports rigorously verifying, archiving, and presenting mathematical proofs. See the FAQ for more information.

Metamath Proof Explorer - Constructs mathematics from scratch, starting from ZFC set theory axioms. Over 40,000 proofs. Theorem list Recent proofs (this mirror)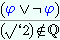

Intuitionistic Logic Explorer - Derives mathematics from a constructive point of view, starting from axioms of intuitionistic logic.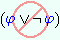

New Foundations Explorer - Constructs mathematics from scratch, starting from Quine's NF set theory axioms.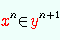

Higher-Order Logic Explorer - Starts with HOL (also called simple type theory) and derives equivalents to ZFC axioms, connecting the two approaches.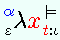

Other Metamath-Related Topics - user-contributed proof verifiers, Metamath 100 list, open problems, other downloads, and miscellany. Filip Cernatescu's Milpgame and practice problems, and also his XPuzzleAndroid app.

Mini FAQ

Q: What is Metamath?
**A:**Metamath is a simple and flexible computer-processable language that supports rigorously verifying, archiving, and presenting mathematical proofs. Metamath has a small specification that enables you to state a collection of axioms (assumptions), theorems, and proofs (aka a "database"). We have databases for several axiomatic systems. Metamath provides precision, certainty, and the elimination of human error. Through Metamath you can see mathematics developed in complete detail from first principles, with absolute rigor, in a way unlike any other system. Hopefully it will amuse you, amaze you, and possibly enlighten you in its own special way.

Q: What is distinctive about Metamath?
Metamath is probably unlike anything you have encountered. Here are some distinctive traits of Metamath:

1. The Metamath language is extremely simple, with an almost total absence of hard-wired syntax. We believe that it provides about the simplest possible framework that allows essentially all of mathematics to be expressed with absolute rigor.
2. Metamath is not tied to any particular set of axioms, instead, axioms are defined in a database.
3. Metamath proofs include every step, no exceptions, where each step is only an application of an axiom or a previously-proved statement. This is different from almost all other computer-verifiable proof systems, which allow statements (like "simp", "auto", or "blast") that don't show the proof steps but instead ask a computer to try to rediscover the proof steps. Metamath's unique approach speeds verification, improves archiving, and enables_anyone_ to follow every proof step.
4. Many tools support Metamath, instead of requiring a "canonical" tool.
5. Metamath verifiers have been independently implemented by different people in different programming languages, reducing the risk of accepting an invalid proof.
6. Metamath's fundamental operation (substitution) is easy to understand, even by those who aren't professional mathematicians.
7. Proofs stay proven. In many systems changes to a system's syntax or tactics cause older proofs to stop being verifiable. Metamath's approach, which cleanly separates proof verification from discovery, provides better support for long-term archives.
8. Metamath is one of the top systems in theFormalizing 100 Theorems challenge. The Metamath Proof Explorer (MPE) database alone has over 23,000 proven theorems.

Of course, other systems may have advantages over Metamath that are more compelling to you. Some users of Metamath also use or develop other systems; we're always delighted to cooperate with other systems' users when we can.

Q: How can I ask questions or discuss Metamath-related topics?
A: The Metamath Google Group mailing list is a great place to discuss Metamath. If you have questions, that is a good place to ask them.

Q: Where do I start?
A: Read Sections 1, 2, and 3 of the Metamath Proof Explorer. Then look at a few proofs in Section 4 to make sure you understand how they work.
Knowledge of mathematics can be helpful, although it isn't strictly necessary to be able to mechanically follow the proofs on this site. If you want to start acquiring a higher-level understanding, a nice independent introduction to logic is Hirst and Hirst's A Primer for Logic and Proof ; compare its axioms to ours. Wikipedia has an overview of set theory.The video series"Introduction to Higher Mathematics" by Bill Shillito may also be helpful.

Q: What kinds of tools support Metamath?
Many tools support Metamath. There are three categories of Metamath tools, though some tools belong to more than one category:

1. Proof assistants help you interactively create proofs.
2. _Verifiers_verify that a database is correct - in particular, that the proofs in a database are correct. There are over a dozen verifiers available. Metamath verifiers do not make logical inferences; they just verify that the proof as stated is correct.
3. _Support and other tools_perform other Metamath-related tasks. Some of these tools are also proof assistants and/or verifiers. For example, the originalmetamath-exe tool is a proof assistant, a verifier, and also provides various support functions such as generating HTML pages.Metamath-knifeis a fast verifier in Rust that also has other capabilities. For more information, see thelist of other tools for Metamath.

Q: What proof assistants support Metamath?
To create new Metamath proofs, you'll want to use a proof assistant. The main Metamath proof assistants are:

1. mmj2 - mmj2 is currently the most commonly-used tool. It's written in Java. David A. Wheeler produced an introductory video, "Introduction to Metamath & mmj2".
2. metamath-lamp -metamath-lamp(Lite Assistant for Metamath Proofs) is a new Metamath proof assistant by Igor Ieskov written in JavaScript. You don't need to install anything to use it, just use your web browser (including your smartphone web browser) to view theMetamath-lamp application page. You can learn to use metamath-lamp from the extensiveMetamath-lamp Guideor theIntroduction to Metamath-lamp videosby David A. Wheeler. Software developers may want to see theMetamath-lamp source code repository.
3. metamath-exe - themetamath-exe program is an ASCII-based ANSI C program with a command-line interface. This is the original program for processing Metamath; today it's it's often called "metamath-exe" to distinguish it from other Metamath tools.
4. yamma - Yamma is a Metamath proof assistant for Visual Studio Code (VS Code). It's implemented as a VS Code extension for Metamath. See the Yamma source repository for more information.

In addition,mmpp is an experimental proof editing environment for the Metamath language by Giovanni Mascellani. See themmpp GitHub project pagefor how to build it under Linux, MacOS, and Windows. See also its Google group announcement.

Q: Will Metamath help me learn abstract mathematics?
**A:**Yes, but probably not by itself. Metamath uses a single, simple substitution rule that allows you to follow any proof mechanically. You can actually jump in anywhere and be convinced that the symbol string you see in a proof step is a consequence of the symbol strings in the earlier steps that it references, even if you don't understand what the symbols mean. But this is different from understanding the meaning of the math that results. Metamath by itself probably will not give you an intuitive feel for abstract math, in the same way it can be hard to grasp a large computer program just by reading its source code, even though you may understand each individual instruction. However, Metamath combined with other materials can be powerful for learning. The Bibliographic Cross-Reference lets you compare informal proofs in math textbooks and see all the implicit missing details "left to the reader."

Q: Who is the intended audience for Metamath?
A: Metamath is not for everyone, of course. A person with no interest in math may find it boring or, optimistically, might find a spark of inspiration. Professional mathematicians may view it as a curiosity more than a tool - they need to do things at a high level to work efficiently. On the other hand, Metamath can appeal to those who enjoy picking things apart to see how they work. Others may like the absolute rigor that Metamath offers. Someone new to logic and set theory, who is still developing the mathematical maturity needed to follow informal textbook proofs, may find some reassurance in Metamath's step-by-step breakdown. And anyone who appreciates the austere elegance of formal mathematics for its own sake might enjoy just casually browsing through the proofs for their aesthetic appeal.

Q: I already have an abstract mathematics background. How can I grasp the key ideas in a Metamath proof more quickly?
A: On the web page with the proof, look at the little colored numbers in the Ref column. The steps with the largest numbers are usually the ones you want to look at first. The steps with smaller numbers are typically logic "glue" to tie them together. The colors follow roughly the rainbow colors as the statement number increases, so that the largest numbers tend to stand out from the others.With a little practice, this feature, together with the gray indentation levels showing the tree structure, should help you figure out the "important" steps so that you could write down an informal version of the proof if you wanted to.By the way, it's best not to use the colored numbers to refer to theorems in an archived discussion, since they change when new theorems are inserted at an earlier point in the database. Instead, just use their names.

Q: What does the Metamath language look like?
A: The precise technical specification of the language is given in Section 4.1 (p. 112) of the Metamath bookand is about 4 pages long. A simple example is given in Section 2.2.2 (p. 40). Compare this source screenshot with the generated web page. As an indication of the language's simplicity, Raph Levien independently wrote the remarkably small mmverify proof verifier in Python. He writes, "I find the whole thing a bit magical. Those 300 lines of code, plus a couple dozen axioms, effectively give you the building blocks for all of mathematics." Bob Solovay wrote a nicely commented presentation of Peano arithmetic in the Metamath language, peano.mm, that is worth reading as a stand-alone file.

However, _you don't have to know or even look at the language_if you just want to follow the proofs (you can just read pages on this website) or create new proofs (you would typically use aproof assistant).

Q: What other programs have been written for the Metamath language?
A: Over a dozen proof verifiers for the Metamath language have been written and are listed atKnown Metamath proof verifiers. Also, several proof languages have been based on Metamath, and the software and other documentation for these can be found underMetamath-related programs.

Q: How confident can I be in the proofs?
A: You can be extremely confident that the proofs follow from their axioms. All reasoning is done directly in the proof itself rather than by algorithms embedded in the verification program. Computer verification programs never get tired and rigorously check every step. There is the risk that a verifier has a programming bug, but this is countered by the Metamath language's small size (this simplicity reduces the likelihood of such bugs) and by using multiple independently-implemented verifiers (since it is unlikely that all verifiers will have the same kind of bug). For example, theMetamath Proof Exploreris routinely checked by 5 independently-created verifiers in 5 different programming languages:metamath (a C verifier by Norm Megill),mmj2 (a Java verifier by Mel O'Cat and Mario Carneiro),smetamath-rs (a high-speed Rust verifier by Stefan O'Rear),checkmm (a C++ verifier by Eric Schmidt).mmverify.pya Python verifier by Raph Levien). In addition, the databases are public and can easily be inspected; the hypertext links in generated proofs make it especially easy to move from one theorem to the next. Metamath enables an extremely rigorous form of peer review.

Q: Why is it called "Metamath"?
A: It means "metavariable math." See A Note on the Axioms. Metamath shouldn't be confused with metamathematics (occasionally abbreviated metamath, metamaths, or meta math), which is a specialized branch of mathematics that studies mathematics itself, leading to results such as Gödel's incompleteness theorem. An expert in the latter is called a metamathematician, so to avoid confusion one might use "metamathician" for someone knowledgeable about Metamath.

Q: Are there other sites that formalize math from its foundations?
A: Another project that aims to rigorously formalize and verify math is Mizar. It is intended to appeal to professional mathematicians and requires a certain mathematical maturity to be able to follow its proofs. It tries to mimic mathematical proofs they way they are normally published, whereas Metamath shows you every detail.
Some other well-known interactive theorem provers areLean,HOL Light, Isabelle,and Coq. Freek Wiedijk wrote an interesting collection of notes comparing several mathematical proof languages. His book, The Seventeen Provers of the World,compares the proofs that the square root of 2 is irrational in 17 proof languages, including Metamath (theorem sqrt2irr). TheMetamath 100 page shows metamath's progress inFormalizing 100 Theorems(a challenge set of theorems for math formalization systems). For comparisons, seewhat is distinctive about Metamath.

Q: How can I contribute to Metamath?
**A:**We'd be delighted if you decide to contribute! The Metamath community has several inter-related projects, so you first need to determine which specific project you want to contribute to. Here are some common cases:

1. If you're contributing to "set.mm" (the set of proofs which starts from ZFC set theory axioms and shown in the "Metamath Proof Explorer"), the recommended approach is to use its GitHub repository at https://github.com/metamath/set.mm(at least as a starting point). For detailed instructions on using GitHub for this project, readGetting started with contributing andCONTRIBUTING.md. In practice you'll probably want to chat on theMetamath mailing list.
2. If you want to modify the mmj2 program (the editor/GUI proof assistant written in Java by Mel O'Cat and enhanced by Mario Carneiro), go to itsmmj2 GitHub repository.
3. If you want to modify the metamath-exe program (the original tool implementation written in C), go to themetamath-exe GitHub repository.
4. If you want to modify a webpage, you'll need to determine its source. Changes to top-level web pages go to themetamath-website-seed GitHub repository. Changes to a specific database go to that database's repository, often the set.mm GitHub repository. The Metamath website is generated by running scripts that combine the current metamath-website-seed and database data. In rare cases you may want to propose changes to those scripts, in which case you can propose them to themetamath-website-scripts GitHub repository.

When in doubt, ask or post your proposal to the metamath mailing list. We would be delighted to help you. If you must contact someone privately, please emailMario Carneiro orDavid A. Wheeler(after removing the NOSPAM markers from the email addresses).

Q: Who was Norman ("Norm") Megill?
**A:**Norman "Norm" Dwight Megill, Ph.D. (1950-2021) was the original creator of Metamath. He created the Metamath language, developed the first tool to support it (now called metamath-exe), and first developed axioms and proofs in this language. For over 30 years he cultivated an international community of people with the shared dream of digitizing and verifying mathematics. His ideas and design have been influential in formal mathematics. He had an interest in the properties of Quantum logic and Hilbert spaces, and used Metamath to formalize his investigations. Norman received his undergraduate degree in Electrical Engineering and Computer Science from MIT in 1972 and his Ph.D. from the University of Zagreb, Croatia in 2010. He died suddenly of natural causes on December 9, 2021, at the age of 71. He issorely missed by all who knew him(obituary). The Metamath system he created lives on and is a fitting memorial to his extensive contributions.

Metamath book

The book**Metamath: A Computer Language for Mathematical Proofs** (248 pp.), written by Norman Megill with extensive revisions by David A. Wheeler, provides an in-depth understanding of the Metamath language, the metamath-exe program, and an introduction to the set.mm database. It is also called the Metamath book. The first part of the book includes an easy-to-read informal discussion of abstract mathematics and computers, with references to other proof verifiers and automated theorem provers.

The Metamath book is available in many forms:

• Metamath book in PDF format (free).
• German translation of the Metamath book in PDF format (free).
• Metamath book narrow width in PDF format (free). This narrow width form is better when reading on small displays such as smartphones,
• Hardcover version of the Metamath book (ISBN 978-0-3597-02237). If you want a physical copy, it's easy to get one! This book was released in 2019 and is labeled second edition. It's available in many other places too, for example, you can getthe Metamath book on Amazon. However, we recommendgetting the Metamath book from Lulu if it doesn't matter to you (it tends to be cheaper and faster to get).
• metamath.texis the LaTeX source file for the book. The comment at the beginning explains the steps for how to compile it.

You can also view the Metamath book errata. The book source is maintained on GitHub athttps://github.com/metamath/metamath-book, which also provides an archive of older editions.

The following BibTeX citation is suggested for the printed version.

@Book{metamath,
author = {Norman D. Megill},
author = {David A. Wheeler},
title = {Metamath: A Computer Language for Mathematical Proofs},
year = {2019},
publisher = {Lulu Press},
address = {Morrisville, North Carolina},
note = {{\tt http://us.metamath.org/downloads/metamath.pdf}},
}

Downloads

• metamath.tar.bz2 (14 MB) ormetamath.tar.gz (17 MB) ormetamath.zip (17 MB)
  • Description: Themetamath-exe (aka "metamath program") is an ASCII-based ANSI C program with a command-line interface. This is the original program for processing Metamath, but since there are many other tools it's typically called "metamath-exe" to distinguish it from other tools.
  • Instructions: 1. Extract all files, which will be contained in a directory called "metamath". 2. For Windows, double-click on "metamath.exe" and type "read set.mm". For Linux/MacOSX/Unix, compile with the command "gcc *.c -o metamath" inside the "metamath" directory, then type "./metamath set.mm" to run.3. For all systems, once in the program, use the "help" command to guide you. Consult the Metamath book (above) for an in-depth understanding.
  • To uninstall: Just delete the "metamath" directory. Nothing else on your system was touched by the installation.
• mmj2.zip(7.2 MB) (latest version, 2.4.1 26-Jan-2016, maintained by Mario Carneiro)
  mmj2-orig.zip(Mel O'Cat's last official version, 11-Oct-2011)
  https://github.com/digama0/mmj2(development repository)
  • Description: Mel O'Cat and Mario Carneiro'smmj2 GUI Proof Assistant for the Metamath language. Includes thorough file validation and proof verification, syntactic parsing of Metamath formulas and many other features.
  • Instructions: Download mmj2jar.zip, unzip and read the enclosed documentation. David A. Wheeler produced two introductory videos "Introduction to Metamath & mmj2" [retrieved 1-Aug-2016] and "Creating Functions in Metamath" [retrieved 1-Aug-2016]. Some documentation is also available at the (now archived) Asteroid Meta wikimmj2 [retrieved 24-May-2016].
  • Quick startup for Windows:
    1. Download mmj2.zip and unzip it (wherever)
    2. Copy the mmj2\mmj2jar directory to C:
    3. Edit C:\mmj2jar\RunParms.txt (with e.g. Notepad).
    3a. The first line will read "LoadFile,set.mm"; change it if necessary to point to your set.mm file.
    3b. Add the following 2 lines immediately above the last line that reads "RunProofAsstGUI" (to improve automation in the proof assistant):
    ProofAsstDeriveAutocomplete, yes
    ProofAsstUseAutotransformations, yes,no,yes
    3c. Add the following 2 lines to the end of the file (to ensure set.mm definitions are sound):
    RunMacro,definitionCheck,ax-*,df-bi,df-clab,df-cleq,df-clel
    *done
    4. Edit C:\mmj2jar\mmj2.bat. Change "-Xmx256M" to "-Xmx512M" (to increase heap space for current set.mm size). Change "C:\metamath" to a directory that exists (to store .mmp worksheets).
    5. Start -> All Programs -> Accessories -> Command Prompt
    6. Type: java then ENTER. If the response is "'java' is not recognized...", you need to install the Java runtime system fromjava.com[retrieved 11-May-2016], then exit and reenter the Command Prompt.
    7. Type:
    CD C:\mmj2jar
    mmj2.bat
  • Notes:
    * The eimm export-import program links the mmj2 and Metamath proof assistants without exiting from either program, giving you the features of both during proof development.
    * The mmj2 directory listing also has the source code, older releases, and MD5 checksums.
• mpeuni.tar.bz2 (70 MB) ormpeuni.tar.gz (140 MB) ormpeuni.zip (180 MB)
  • Description: The complete set ofMetamath Proof Explorer web pages. Includes the Hilbert Space Explorer and the Metamath Music Page. (Does not include the GIF version of the pages.)
  • Instructions: Extract all files (around 35,000) into a directory called "mpeuni". The home page is the file "mmset.html". You will need about 3.5 GB of free space.
• qleuni.tar.bz2 (1 MB) orqleuni.tar.gz (2 MB) orqleuni.zip (4 MB)
  • Description: The complete set of Quantum Logic Explorer web pages.
  • Instructions: Extract all files (around 1,000) into a directory called "qleuni". The home page is the file "mmql.html".
• mmsolitaire.tar.bz2 (0.2 MB) ormmsolitaire.tar.gz (0.2 MB) ormmsolitaire.zip (0.3 MB)
  • Description: The Metamath Solitaire web page, compiled Java applet, and applet source code.
  • Instructions: Extract all files into a directory called "mmsolitaire". Use the page "mms.html" to run the applet.
• symbols.tar.bz2 (0.2 MB) orsymbols.tar.gz (0.3 MB) orsymbols.zip (0.8 MB)
  • Description: A collection of over 1,000 mathematical symbols in the form of transparent GIFs that you can use on your own web pages.
  • Instructions: Extract all files into a directory called "symbols". The home page is the file "symbols.html".
• mmverify.py (version of 27-Jan-2013) (previous version)
  • Description: Raph Levien's independently-written Pythonproof verifier for the Metamath language.
  • Instructions: See the comments at the top of the program listing.
• eimm.zip (0.1 MB)
  • Description: An experimentalproof export-import program (version 0.08 23-Mar-2021) that translates incomplete proofs in progress between the Metamath program's CLI Proof Assistant and Mel O'Cat's mmj2GUI Proof Assistant, without exiting from either proof assistant, giving you the features of both assistants during proof development.
  • Instructions: Extract all files into a directory called "eimm". See the readme.txt file for detailed instructions. A pre-compiled Windows binary is provided; gcc is required to compile for Linux/MacOSX/Unix. Metamath program's Proof Assistant (MM-PA> prompt)
    | ^
    | |
    submit eimmexp.cmd /s submit eimmimp.cmd /s
    | |
    v |
    [*.mmp proof worksheet file]
    | ^
    | |
    File/Open File/Save
    | |
    v |
    mmj2 GUI Proof Assistant
  • Status: There are no known bugs. The development of this prototype is believed to be complete. The only change in the future might be to incorporate the import-export algorithms natively as Metamath program commands, for convenience. Suggestions for other possible features are, of course, welcome.
• finiteaxiom.pdf (0.2 MB)
  • Description: Preprint of thearticle "A Finitely Axiomatized Formalization of Predicate Calculus with Equality," which provides the theoretical basis for Metamath and is referenced on the Metamath Proof Explorer pages. [This PDF file was generated from the LaTeX source file finiteaxiom.tex (0.1 MB).] The correspondence between the axioms in this paper and the ones in the set.mm database is described inAppendix 8 of the Metamath Proof Explorer Home Page. See technical note 1 for some additional notes.
• weakd.pdf (0.2 MB)
  • Description: The article "Weaker D-Complete Logics," which is referenced in the Metamath Solitaire applet.
• Quantum logic papers
  • Description: Several papers on quantum logic, orthomodular lattices, and Hilbert space can be downloaded from here.
• quantum-logic.tar.bz2 (0.05 MB) orquantum-logic.tar.gz (0.1 MB) orquantum-logic.zip (0.1 MB)
  • Description: Severalprograms (lattice.c, latticeg.c, beran.c, bercomb.c) referenced in the papers "Algorithms for Greechie Diagrams" and "Orthomodular Lattices and a Quantum Algebra."
  • Instructions: Extract all files into a directory called "quantum-logic". See the README.TXT file therein for instructions on compiling and using the programs. You will need a C compiler such as gcc.
  • Note:
    * The above programs are frozen at the versions used for the papers and will reproduce the papers' results exactly.Each .c file is a stand-alone program. After compiling (under Linux/Cygwin/MacOSX/Unix) with "gcc program.c -o program", type "./program --help" for instructions.
• metamathsite.zip (171 MB)
  • _Description:_A mirror of the entire Metamath web siteincluding all the downloads listed above (that aren't external links). This can be useful if you have a slow connection or want to browse the site off-line. A script builds the site from source files and requires a Linux/MacOSX/Unix operating system (or the free Cygwin[retrieved 4-Aug-2016] for Windows). About 9 GB of disk space will be needed.
  • _Instructions:_Extract all files into a directory called "metamathsite". Go to that directory then type "./install.sh". This may take several hours to run. The home page (this page) will be "index.html".
    * In Cygwin, to go to a directory, type "cd c:/tmp/metamathsite" if your directory (folder) is C:\tmp\metamathsite.
    * On MacOSX, select the Terminal application from Applications/Utilities to get to the command line.
  • To uninstall: Just delete the "metamathsite" directory. Nothing else on your system was touched by the installation.
  • Notes:
    * See the <README.TXT> file that accompanies the download for more detailed instructions.
    * Another way to install your local copy is with rsync (on Linux/MacOSX/Unix or Cygwin). The download will be compressed to about 2GB and automatically expanded to about 3.5GB. Create and go to the metamathsite directory, then type (including the last period):
    rsync -vrltS -z --delete --delete-after rsync://rsync.metamath.org/metamath .
    Rerunning this same command periodically will also keep your copy updated, downloading only the files that changed. Note that you need twice the disk space during rsync, i.e. 7GB.
    * A third way to install your local copy is with wget (see the Download and Extraction Help below). The full uncompressed 3.5GB site will be downloaded, so it will take a long time, depending on your connection speed. Create and go to the metamathsite directory, then type:
    wget -nH --mirror "http://us.metamath.org/index.html"
    * If you would like to set up a mirror site for public access, read the instructions in <mirror.txt>.

Note: Some of the links in the section below are obsolete. Let me know if you have current links. --NM 16-Feb-2013

Reviews
The Assayer open-content book reviews (Jan. 8, 2004)	University of WaterlooArchimedes' Sandbox Reviews (Oct. 28, 2002)	Multimedia Education Resource for Learning and Online Teaching (Jul. 21, 1997)
Also: John Bethencourt,Principia Mathematica Revisited (Jan. 24, 2004)
Also: American Scientist,Metamath (site of the week) review (Jul. 25, 2005) [retrieved 6-Jul-2016]
Also: University at Albany Science Library, 2007 Top 30 Science Resources (Dec. 20, 2007)

Directories
Wikipedia	Drexel University's Math Forum Internet Mathematics Library (anothermention)
Government of Australia Education Portal	Encyclopædia Britannica "approved iGuide site" (Oct. 11, 2006) (freeset theoryfull text article)
Awards
The Golden House Sparrow Award: Site of the Day (Jul. 20, 2000) (check out their eclectic current page)	Scout Report for Science and Engineering Selection (Jul. 19, 2000)
Knot a Braid of Links "Cool math site of the week" (Jul. 7-13, 1998)	Rated by JARS (Apr. 26, 1998)

This page was last updated on 17-Nov-2024.

Copyright terms for this page:Public domain except the images below "Reviews"

(Hidden files)