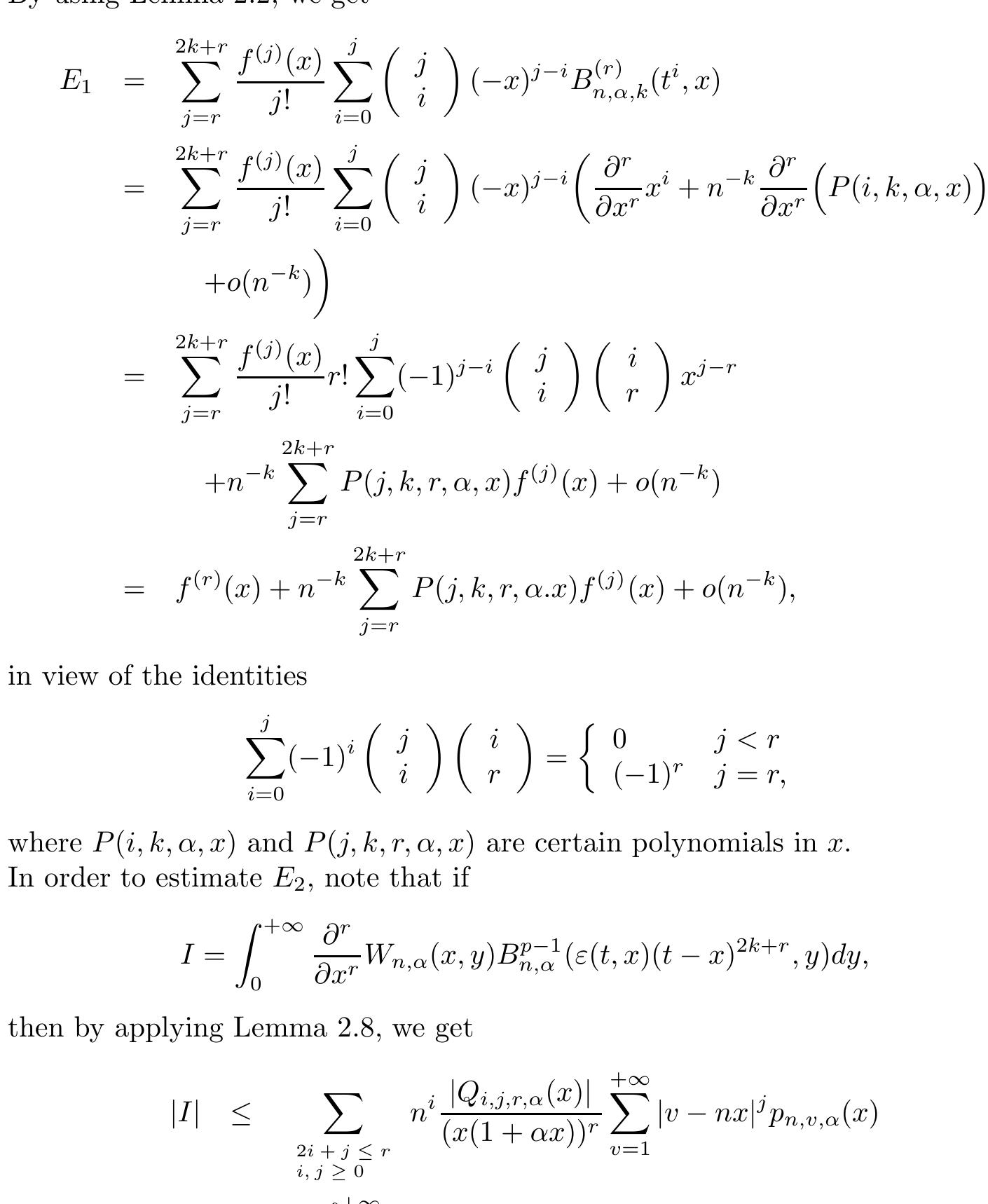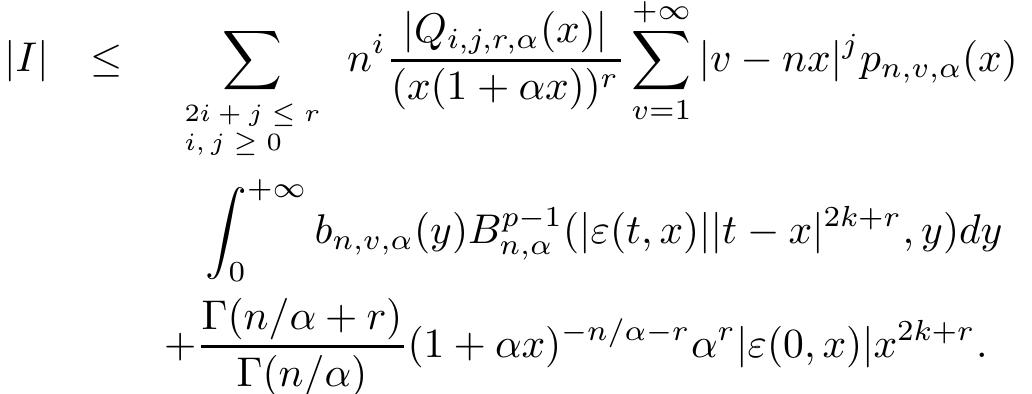Simultaneous Approximation for Generalized Baskakov-Durrmeyer-Type Operators (original) (raw)
Abstract
The present paper deals with the study of a Durrmeyer-type integral modification of certain modified Baskakov operators. Here we study simultaneous approximation properties for these operators by using the iterative combinations. We obtain an asymptotic formula and an error estimation in terms of higher order modulus of continuity for these operators.
FAQs
AI
What are the main properties of the new Baskakov-Durrmeyer operators introduced?add
The newly defined Baskakov-Durrmeyer operators reproduce both constants and linear functions, unlike traditional operators.
How does the order of approximation for these operators compare to existing methods?add
The paper demonstrates that the order of approximation is O(n^{-1}), consistent even for smooth functions.
What is the role of iterative combinations in improving approximation accuracy?add
Iterative combinations, as proposed by Micchelli, enhance the order of approximation beyond standard limits.
What asymptotic behaviors or error estimations are derived in the research?add
The study establishes Voronovskaja-type formulas and provides error estimations for the operators' iterative combinations.
How does this work extend previous studies on generalized Baskakov-type operators?add
This work builds on Wang Li's research, addressing operators that reproduce linear functions, previously unconsidered.
Figures (5)
Proof of Theorem 1.1. By applying Lemma 2.9, we get
Proof of Theorem 1.2. By Taylor expansion of f, we have
The second term in the right hand side of above expression multiplied by n* tends to zero as n — +00. Since e(t,7) > 0 as t > a, for a given ¢ > 0 there exists a 0 > 0, such that |e(t,x)| < ¢ whenever 0 < |t — 2| < 6. Also, for |é — 2| > 4, we have |e(t,x)(t — «)?**"| < M(1+t)7 for some M > 0, since we can consider

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
References (10)
- P.N. Agrawal and A.J. Mohammad, Approximation by iterative combinations of a new sequence of linear positive operators. In: Advances in Constructive Approximation (Vanderbilt 2003), Mod. Methods Math. Nashboro Press, Brentwood, TN, 2004, 13- 24.
- Z. Finta, On converse approximation theorems. J. Math. Anal. Appl. 312 (2005), 159- 180.
- S. Goldberg and V. Meir, Minimum moduli of ordinary differential operators. Proc. London Math. Soc. 23 (1971), 1-15.
- N.K. Govil and V. Gupta, Direct estimates in simultaneous approximation for Dur- rmeyer type operators. Math. Inequal. Appl. (to appear).
- V. Gupta, Approximation for modified Baskakov Durrmeyer type operators. Rocky Mountain J. Math. (to appear).
- Vol. 4 (2007) Simultaneous Approximation 495
- V. Gupta, M.A. Noor, M.S. Beniwal and M.K. Gupta, On simultaneous approximation for certain Baskakov Durrmeyer type operators. JIPAM. J. Inequal. Pure Appl. Math. 7 (2006), 1-15.
- W. Li, The Voronovskaja type expansion formula of the modified Baskakov-Beta op- erators. J. Baoji University of Arts and Science (Natural Science Edition) 25 (2005), 94-97, 479-492.
- C.A. Micchelli, Saturation class and iterates of the Bernstein polynomials. J. Approx. Theory 8 (1973), 1-18.
- H.M. Srivastava and V. Gupta, A certain family of summation integral type operators. Math. Comput. Modelling 37 (2003), 1307-1315.