High order accurate solution of the incompressible Navier–Stokes equations (original) (raw)
Abstract
High order methods are of great interest in the study of turbulent flows in complex geometries by means of direct simulation. With this goal in mind, the incompressible Navier-Stokes equations are discretized in space by a compact fourth order finite difference method on a staggered grid. The equations are integrated in time by a second order semi-implicit method. Stable boundary conditions are implemented and the grid is allowed to be curvilinear in two space dimensions. In every time step, a system of linear equations is solved for the velocity and the pressure by an outer and an inner iteration with preconditioning. The convergence properties of the iterative method are analyzed. The order of accuracy of the method is demonstrated in numerical experiments. The method is used to compute the flow in a channel, the driven cavity and a constricted channel.
FAQs
AI
What advantages does the proposed method have over spectral methods?add
The proposed method retains high accuracy while applying to complex geometries, unlike spectral methods, which are limited to simple structures. Numerical tests indicate that it achieves fourth order spatial accuracy with fewer grid points compared to second order methods.
How does the proposed discretization handle boundary conditions effectively?add
The method applies stable boundary conditions that avoid nonuniqueness in pressure, allowing for consistent solutions. No additional numerical boundary conditions are necessary for pressure due to the staggered grid arrangement.
What findings were observed regarding timestep constraints in the simulation?add
Timestep constraints were identified, indicating that a lower CFL-number around 0.5 to 1 is necessary for accuracy in turbulent flow scenarios. Larger timesteps reduce computational efficiency in transitional flow regimes.
What method is utilized for solving the linear system in each timestep?add
An iterative method is employed for solving the linear equations in each timestep, incorporating preconditioning via incomplete LU factorization to enhance convergence rates. On average, only one or two outer iterations are needed for satisfactory convergence.
How was accuracy verified in numerical experiments presented in the study?add
Accuracy was verified across several geometries, including a driven cavity and a constricting channel, where errors were compared against known solutions. The method demonstrated expected convergence rates, achieving fourth order spatial accuracy.
Figures (17)
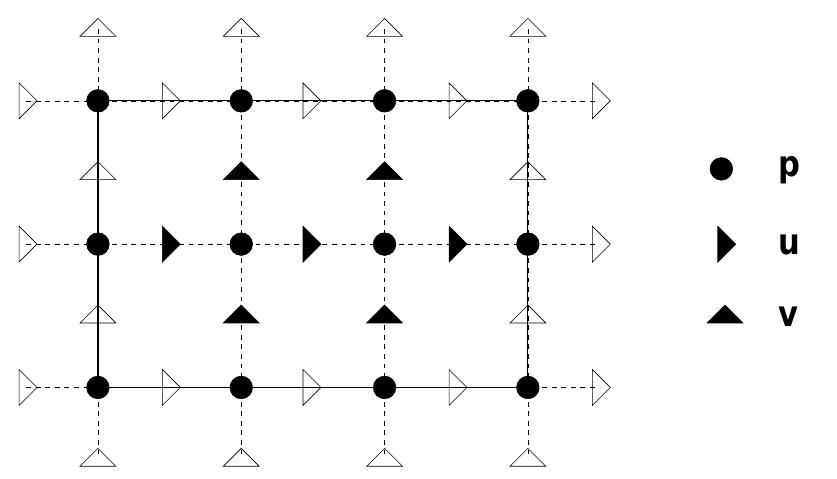
Figure 1: The staggered grid. The boundary is marked by a solid line, the inner points in the grid have filled symbols, and variables at the empty symbols are determined by the boundary conditions.
In order to solve for the unknowns f’, we need closed systems of the form Pf' = Qf for the regular grids and Rf’ = Sf for the staggered grids. No bound- ary conditions are available for the derivatives, and we use one-sided formulas for them. For the function itself on the right hand side of (7) and (8), we could use the physical boundary conditions. However, it is convenient to define P,Q, R,S independently of the particular problem, and therefore we use one-sided formulas also for f, see [4], [5], [20], [34]. ie ey 0 ry a: a i, ry : re fy es ce ee 17
The Laplace operators L¢ and L,, are
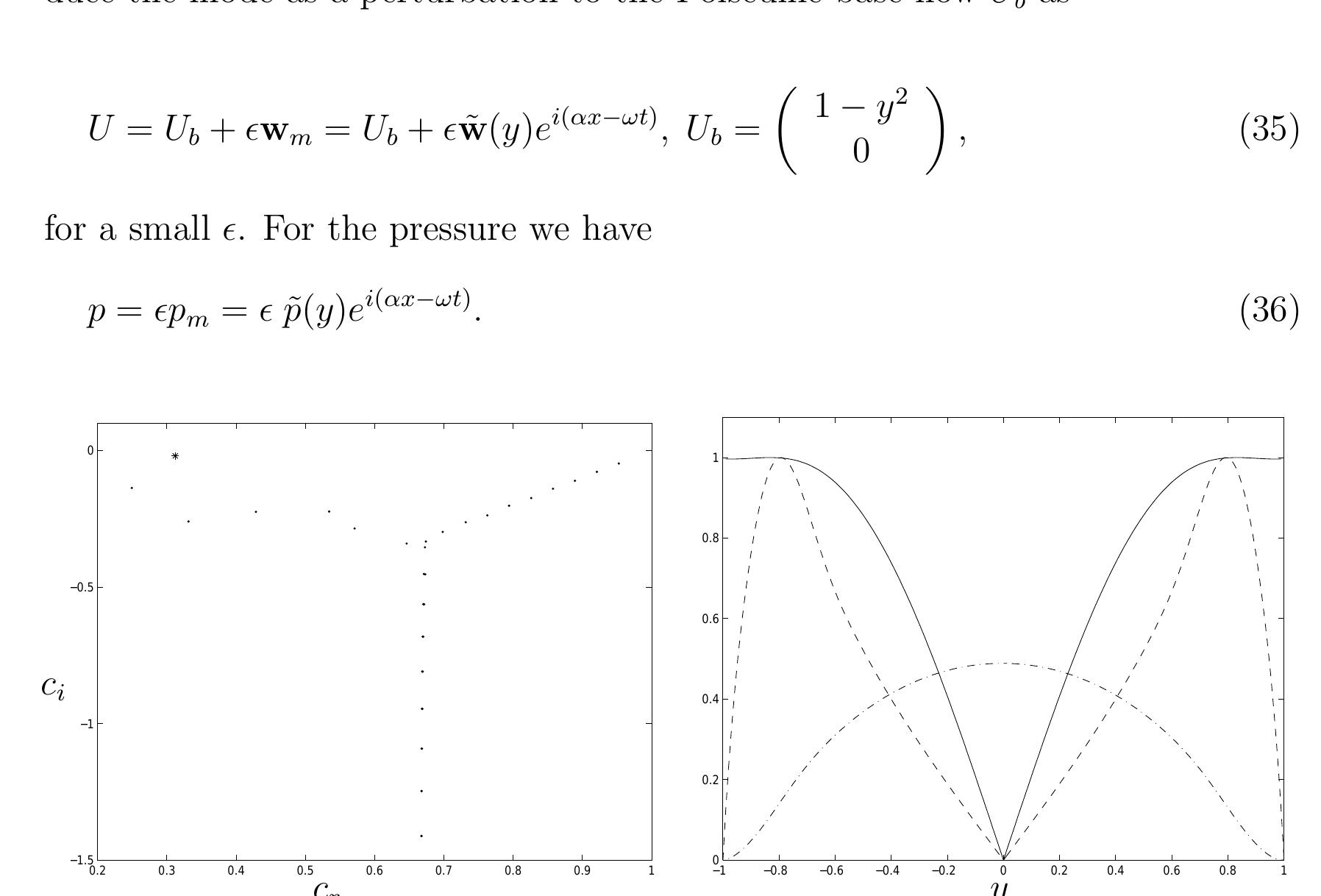
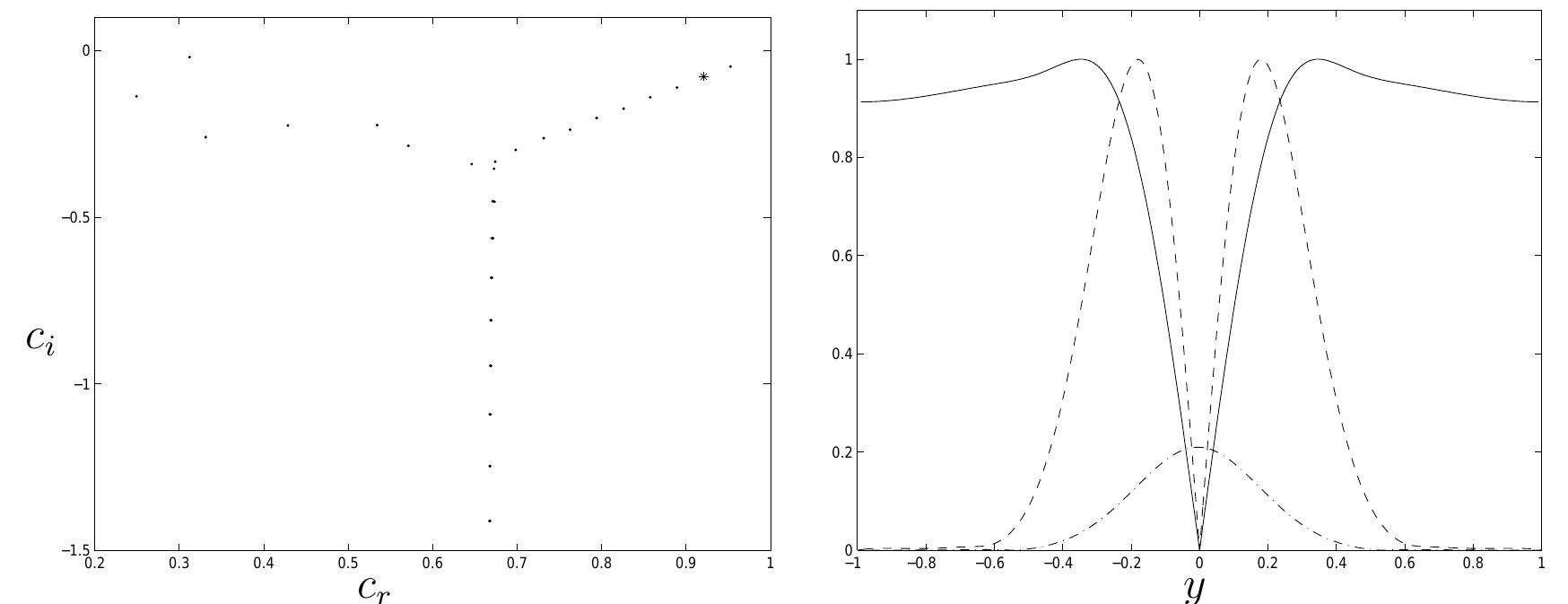
Figure 2: Eigenvalues (left) for 2D Orr-Sommerfeld modes in plane Poiseuille flow at Re = 2000, a = 1. Shape (right) of the normalized, absolute eigenfunc- tions of velocities u (dashed), v (dash-dotted) and pressure (solid) of the mode corresponding to the eigenvalue marked with x. For plane 2D Poiseuille flow, an eigenmode (wW,,, Pm) is of the form
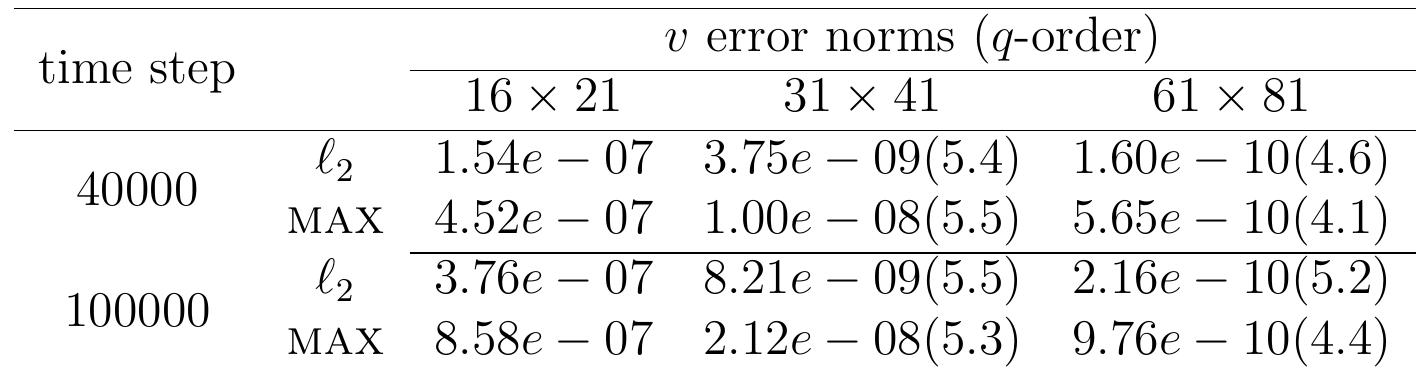
Table 1: Orr-Sommerfeld solutions for 2D Poiseuille flow. The spatial errors ir uw measured in the @, and maximum norms and order of accuracy are shown.
Table 2: Orr-Sommerfeld solutions for 2D Poiseuille flow. The spatial errors in ¢ measured in the £2 and maximum norms and order of accuracy are shown.
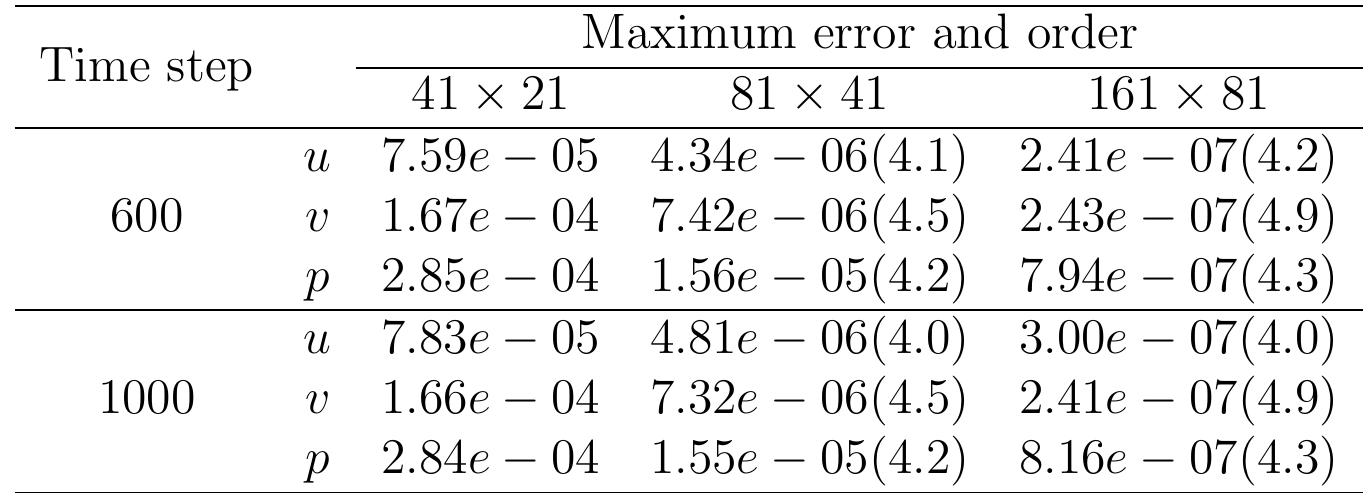
Table 4: Time accuracy at T’ = 5.0. The temporal error is measured in the maximum norm and the order of the error is computed.
Figure 3: Eigenvalues (left) for 2D Orr-Sommerfeld modes in plane Poiseuille flow at Re = 2000, a = 1. Shape (right) of normalized, absolute eigenfunc- tions of velocities u (dashed), v (dash-dotted) and pressure (solid) of the mode corresponding the eigenvalue marked with x.
nq The Navier-Stokes equations are solved for the driven cavity problem. This is a standard problem on a two-dimensional square [0, 1] x [0, 1] with a Cartesian grid. nq The steady flow is computed in a closed cavity with a prescribed velocity at the upper wall y = 1. The streamlines of the solution at two different Re are found in Fig. 4. The steady state is reached by integrating the time-dependent equation until the time-derivatives are sufficiently small. Only one outer iteration in the iterative method is needed in the time steps.
Figure 5: The computed solution for u at Re = 5000 (solid lines) is compared with results from [15] (0) along x = 0.5 on a 41 x 41 grid (left) and on a 81 x 81 grid (right).
Figure 6: The computed solution for v at Re = 5000 (solid lines) is compared with results from [15] (0) along y = 0.5 on a 41 x 41 grid (left) and on a 81 x 81 grid (right).
Figure 7: Grid of the constricting channel geometry . is a ‘twilight-zone flow’ solution [22] with a suitable forcing right hand side in the momentum equation (1). The same solution is chosen in [40]. The velocity is divergence free in (42). The solution for Re = 100 is computed on grids with different resolution and compared with the exact solution (42). The spatial accuracy is evaluated as in (38) and the Tables 1, 2 and 3. The timestep At = 10-° is small to let the space error dominate.
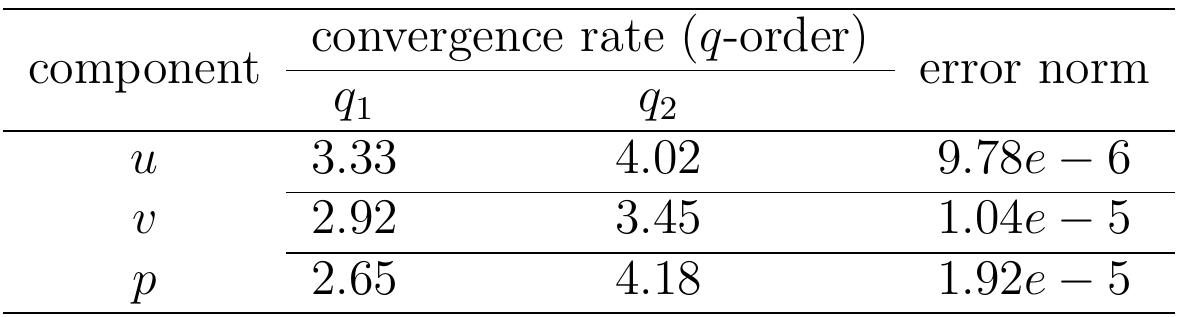
Table 5: Spatial errors and convergence rates measured in the @; norm of the forced solution in the constricting channel at Re = 100
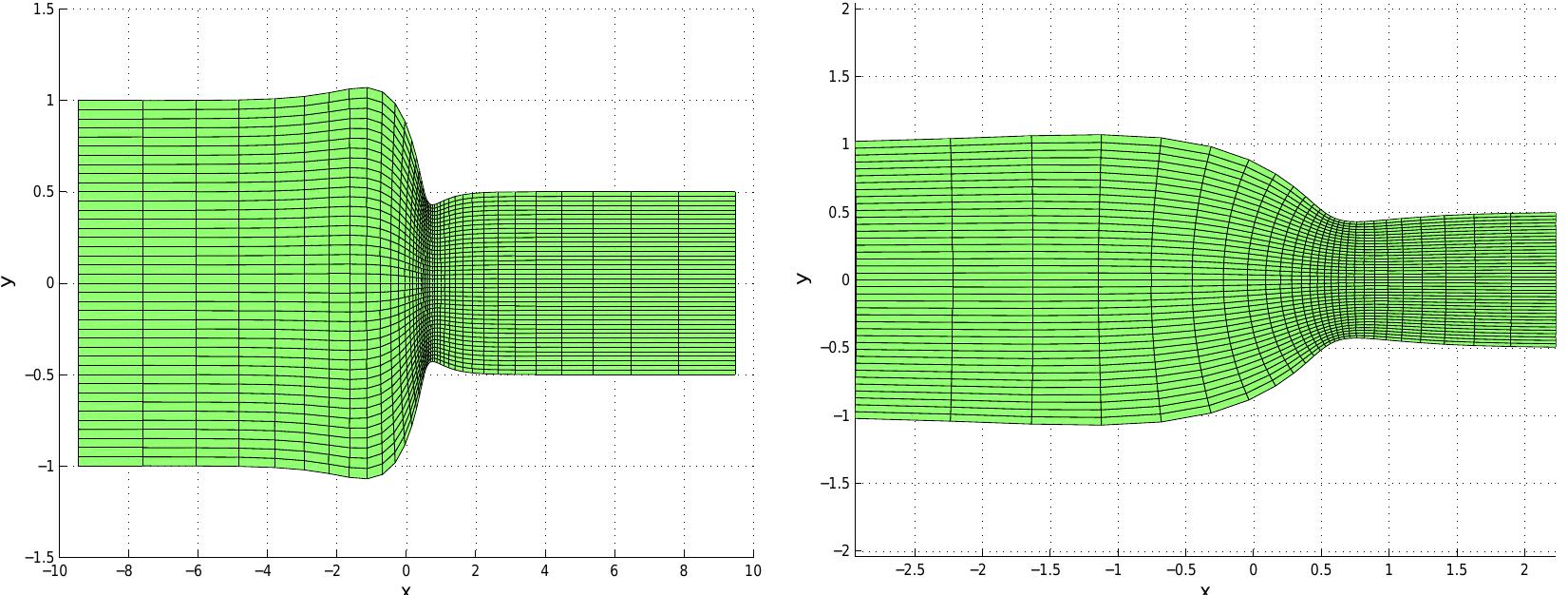
Figure 8: Grid of the constricting channel geometry. The full computational domain (left) and the area around the constriction (right) with equal scaling of the axes. 4.4 Unforced solution in a constricting channel
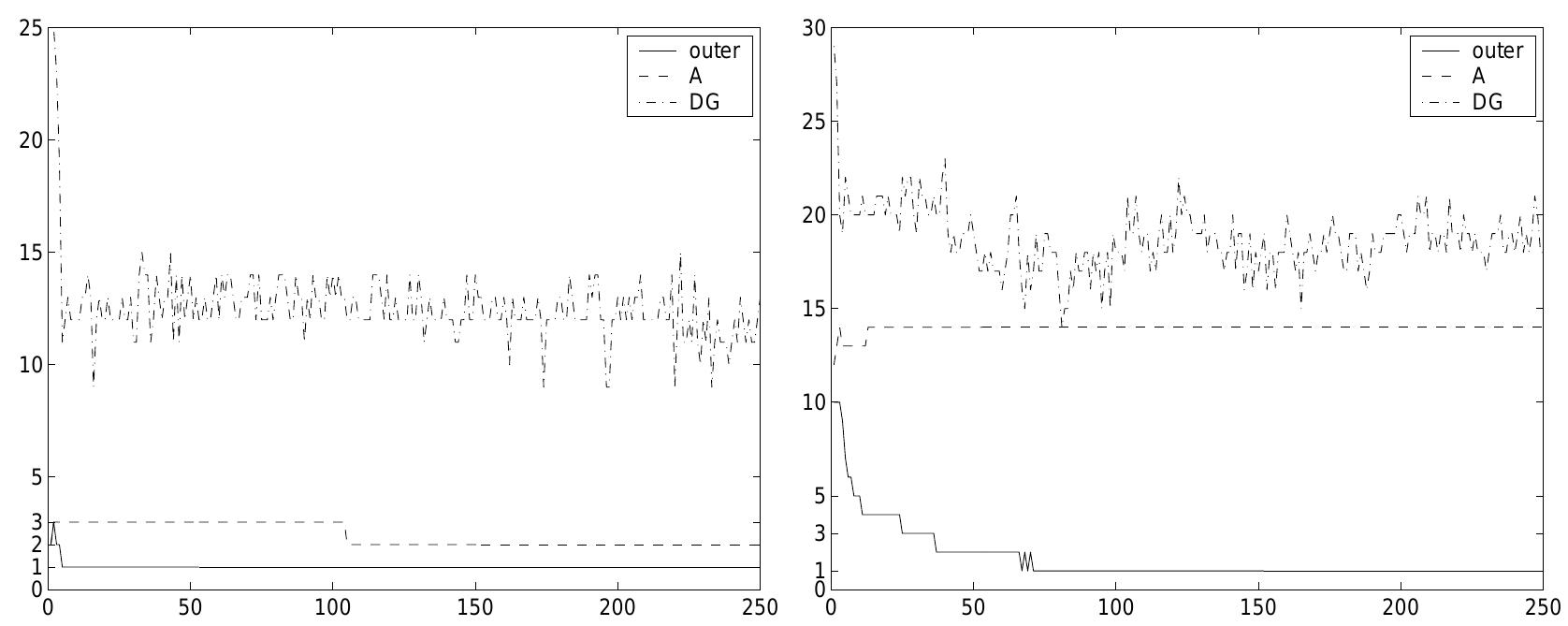
Table 6: Spatial convergence rates and estimates of the numerical error on 81 x 81 grid measured in the @; norm for laminar flow in the constricting channel at Re = 150 The convergence history of the outer and inner iterations (22), (24) and (25) is presented in Fig. 9. The performance is displayed for a long time step and a strict tolerance and a short time step and a tolerance at about 1/2 of the accuracy in the solution in Table 6. The initial solution in the interior is the constant zero solution. This is then integrated for the next 250 steps with Dirichlet inflow conditions and Neumann outflow conditions on the velocity (12). The number of outer iterations is 1 in most of the time steps. The solution of (24) is less efficient
for a smaller ¢ and a larger At as expected from (30). The most time consuming part is the solution of the Poisson-like equation (25). This part is not sensitive to changes in At and the increase in number of iterations from the left to the right figure in Fig. 9 is caused by the decrease in ¢. To improve the efficiency of the method, the focus should be on reducing the computing time spent on the solution of (25). An accurate discretization of the incompressible Navier-Stokes equations in the primitive variables has been developed for two space dimensions. The method can be extended in the third dimension by a spectral approximation without too much difficulty. It is of fourth order accuracy in space and of second order in time in all variables. These orders have been verified in numerical experiments including curvilinear grids. The boundary conditions have been proved to be stable for Cartesian grids and are so in practice also for non-Cartesian grids. The compact difference operators simplify the treatment at the numerical boundaries and no extra numerical boundary conditions are needed for the pressure. The variables are located in a staggered grid to improve the accuracy and to make the method less prone to oscillatory behavior. A system of linear equations is solved in every time step using outer and inner iterations with preconditioning of the subproblems. The difficulty with the nonuniqueness of the pressure and a singular system matrix is avoided by the definition of the boundary conditions. The outer iterations are preconditioned by an approximate factorization with control of the iteration errors.

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
References (44)
- O. Axelsson, Iterative Solution Methods, Cambridge Univ. Press, Cam- bridge, 1994.
- K. Bhaganagar, D. Rempfer, J. Lumley, Direct numerical simulation of spatial transition to turbulence using fourth-order vertical velocity second- order vertical vorticity formulation, J. Comput. Phys., 180 (2002), 200-228.
- D. L. Brown, R. Cortez, M. L. Minion, Accurate projection meth- ods for the incompressible Navier-Stokes equations, J. Comput. Phys., 168 (2001), 464-499.
- A. Brüger, Higher order methods suitable for direct numerical simulation of flows in complex geometries, Licentiate thesis, Dept of Mechanics, Royal Institute of Techonolgy, Stockholm, Sweden, 2002.
- A. Br üger, J. Nilsson, W. Kress, A compact higher order finite differ- ence method for the incompressible Navier-Stokes equations, J. Sci. Com- put., 17 (2002), 551-560.
- J. Cahouet, J.-P. Chabard, Some fast 3D finite element solvers for the generalized Stokes problem, Int. J. Numer. Meth. Fluids, 8 (1988), 869-895.
- W. Chang, F. Giraldo, B. Perot, Analysis of an exact fractional step method, J. Comput. Phys., 180 (2002), 183-199.
- H. Choi, P. Moin, Effects of the computational time step on numerical solutions of turbulent flow, J. Comput. Phys., 113 (1994), 1-4.
- J. K. Dukowicz, A. S. Dvinsky, Approximate factorization as a high order splitting for the implicit incompressible flow equations, J. Comput. Phys., 102 (1992), 336-347.
- H. C. Elman, Preconditioners for saddle point problems arising in compu- tational fluid dynamics, Appl. Numer. Math., 43 (2002), 75-89.
- H. C. Elman, V. E. Howle, J. N. Shadid, R. S. Tuminaro, A paral- lel block multi-level preconditioner for the 3D incompressible Navier-Stokes equations, J. Comput. Phys., 187 (2003), 504-523.
- H. C. Elman, D. J. Silvester, A. J. Wathen, Performance and analysis of saddle point preconditioners for the discrete steady-state Navier-Stokes equations, Numer. Math., 90 (2002), 665-688.
- B. Fornberg, M. Ghrist, Spatial finite difference approximations for wave-type equations, SIAM J. Numer. Anal., 37 (1999), 105-130.
- R. Friedrich, T. J. H üttl, M. Manhart, C. Wagner, Direct numer- ical simulation of incompressible turbulent flows, Computers & Fluids, 30 (2001), 555-579.
- U. Ghia, K. N. Ghia, C. T. Shin, High Re solutions for incompressible flow using the Navier-Stokes equation and multigrid methods, J. Comput. Phys., 48 (1982), 387-411.
- S. Ghosal, An analysis of numerical errors in large-eddy simulations of turbulence, J. Comput. Phys., 125 (1996), 187-206.
- A. Greenbaum, Iterative Methods for Solving Linear Systems, SIAM, Philadelphia, 1997.
- B. Gustafsson, P. L ötstedt, A. G öran, A fourth order difference method for the incompressible Navier-Stokes equations, in M.M. Hafez, ed- itor, Numerical simulations of incompressible flows , World Scientific Pub- lishing, Singapore, 2003, 263-276.
- B. Gustafsson, J. Nilsson, Boundary conditions and estimates for the steady Stokes equations on staggered grids, J. Sci. Comput., 15 (2000), 29- 54.
- B. Gustafsson, J. Nilsson, Fourth order methods for the Stokes and Navier-Stokes equations on staggered grids, in D. A. Caughey, M. M. Hafez, editors, Frontiers of Computational Fluid Dynamics -2002, World Scientific Publishing, Singapore, 2002, 165-179.
- E. Hairer, S. P. Nørsett, G. Wanner, Solving Ordinary Differential Equations I, Nonstiff Problems, 2nd ed., Springer-Verlag, Berlin, 1993.
- W. D. Henshaw, A fourth-order accurate method for the incompressible Navier-Stokes equations on overlapping grids, J. Comput. Phys., 113 (1994), 13-25.
- G. E. Karniadakis, M. Israeli, S. A. Orszag, High-order splitting methods for incompressible Navier-Stokes equations, J. Comput. Phys., 97 (1991), 414.
- J. Kim, P. Moin, Application of a fractional-step method to incompressible Navier-Stokes equations, J. Comput. Phys., 59 (1985), 308-323.
- W. Kress, J. Nilsson, Boundary conditions and estimates for the lin- earized Navier-Stokes equations on a staggered grid, Computers & Fluids, 32 (2003), 1093-1112.
- S. K. Lele, Compact finite difference schemes with spectral-like resolution, J. Comput. Phys., 103 (1992), 16-42.
- M. Li, T. Tang, B. Fornberg, A compact fourth-order finite difference scheme for the steady incompressible Navier-Stokes equations, Int. J. Nu- mer. Meth. Fluids, 20 (1995), 1137-1151.
- A. Lundbladh, D. S. Henningson, A. V. Johansson, An efficient spectral integration method for the solution of the time-dependent Navier- Stokes equations, Report FFA-TN 1992-28, Aeronautical Research Institute of Sweden, Bromma, Sweden, 1992.
- P. F. De A. Mancera, R. Hunt, Fourth order method for solving the Navier-Stokes equations in a constricting channel, Int. J. Numer. Meth. Flu- ids, 25 (1997), 1119-1135.
- J. A. Meijerink, H. A. van der Vorst, An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix, Math. Comp., 31 (1977), 148-162.
- R. S. Montero, I. M. Llorente, M. D. Salas, Robust multigrid al- gorithms for the Navier-Stokes equations, J. Comput. Phys., 173 (2001), 412-432.
- Y. Morinishi, T. S. Lund, O. V. Vasilyev, P. Moin, Fully conservative higher order finite difference schemes for incompressible flow, J. Comput. Phys., 143 (1998), 90-124.
- S. Nagarajan, S. K. Lele, J. H. Ferziger, A robust high-order com- pact method for large eddy simulation, J. Comput. Phys., 191 (2003), 392- 419.
- J. Nilsson, Initial-boundary-value problems for the Stokes and Navier- Stokes equations on staggered grids, PhD thesis, Dept of Scientific Com- puting, Uppsala University, Uppsala, Sweden, 2000.
- M. Ofstad Henriksen, J. Holmen, Algebraic splitting for incompress- ible Navier-Stokes equations, J. Comput. Phys., 175 (2002), 438-453.
- M. Pernice, M. D. Tocci, A multigrid-preconditioned Newton-Krylov method for the incompressible Navier-Stokes equations, SIAM J. Sci. Com- put., 23 (2001), 398-418.
- J. B. Perot, An analysis of the fractional step method, J. Comput. Phys., 108 (1993), 51-58.
- N. A. Petersson, Stability of pressure boundary conditions for Stokes and Navier-Stokes equations, J. Comput. Phys., 172 (2001), 40-70.
- P. J. Schmid, D. S. Henningson, Stability and Transition in Shear Flows, Springer, New York, 2001.
- J. C. Strikwerda, High-order-accurate schemes for incompressible viscous flow, Int. J. Numer. Meth. Fluids, 24 (1997), 715-734.
- J. C. Strikwerda, Y. S. Lee, The accuracy of the fractional step method, SIAM J. Numer. Anal., 37 (1999), 37-47.
- S. Turek, A comparative study of time-stepping techniques for the incom- pressible Navier-Stokes equations: From fully implicit non-linear schemes to semi-implicit projection methods, Int. J. Numer. Meth. Fluids, 37 (1999), 37-47.
- A. Veneziani, Block factorized preconditioners for high-order accurate in time approximation of the Navier-Stokes equations, Numer. Meth. Part. Diff. Eq., 19 (2003), 487-510.
- H. A. van der Vorst, BiCGSTAB: A fast and smoothly converging vari- ant of Bi-CG for the solution of nonsymmetric linear systems, SIAM J. Sci. Comput., 13 (1992), 631-644.
![In order to solve for the unknowns f’, we need closed systems of the form Pf' = Qf for the regular grids and Rf’ = Sf for the staggered grids. No bound- ary conditions are available for the derivatives, and we use one-sided formulas for them. For the function itself on the right hand side of (7) and (8), we could use the physical boundary conditions. However, it is convenient to define P,Q, R,S independently of the particular problem, and therefore we use one-sided formulas also for f, see [4], [5], [20], [34]. ie ey 0 ry a: a i, ry : re fy es ce ee 17](https://figures.academia-assets.com/46699672/figure_002.jpg) ](
](


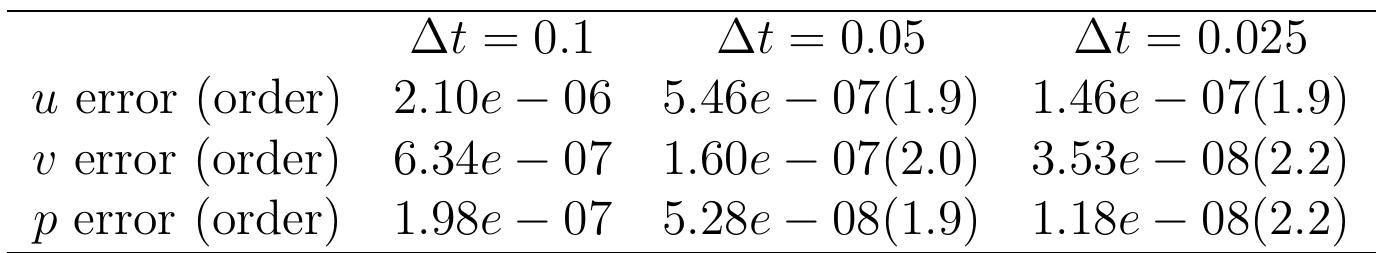
![nq The Navier-Stokes equations are solved for the driven cavity problem. This is a standard problem on a two-dimensional square [0, 1] x [0, 1] with a Cartesian grid. nq The steady flow is computed in a closed cavity with a prescribed velocity at the upper wall y = 1. The streamlines of the solution at two different Re are found in Fig. 4. The steady state is reached by integrating the time-dependent equation until the time-derivatives are sufficiently small. Only one outer iteration in the iterative method is needed in the time steps.](https://figures.academia-assets.com/46699672/figure_006.jpg) ](
](![Figure 5: The computed solution for u at Re = 5000 (solid lines) is compared with results from [15] (0) along x = 0.5 on a 41 x 41 grid (left) and on a 81 x 81 grid (right).](https://figures.academia-assets.com/46699672/figure_007.jpg) ](
](![Figure 6: The computed solution for v at Re = 5000 (solid lines) is compared with results from [15] (0) along y = 0.5 on a 41 x 41 grid (left) and on a 81 x 81 grid (right).](https://figures.academia-assets.com/46699672/figure_008.jpg) ](
](![Figure 7: Grid of the constricting channel geometry . is a ‘twilight-zone flow’ solution [22] with a suitable forcing right hand side in the momentum equation (1). The same solution is chosen in [40]. The velocity is divergence free in (42). The solution for Re = 100 is computed on grids with different resolution and compared with the exact solution (42). The spatial accuracy is evaluated as in (38) and the Tables 1, 2 and 3. The timestep At = 10-° is small to let the space error dominate.](https://figures.academia-assets.com/46699672/figure_009.jpg) ](
](