Chaotic mixing by longitudinal vorticity (original) (raw)
Abstract
Computational fluid dynamics study of the chaotic advection flow in static mixer. Mixing enhancement by using longitudinal vortex generator. Poincaré sections and the Lagrangian trajectories show that chaotic advection takes place in the alternated configuration.
Figures (15)
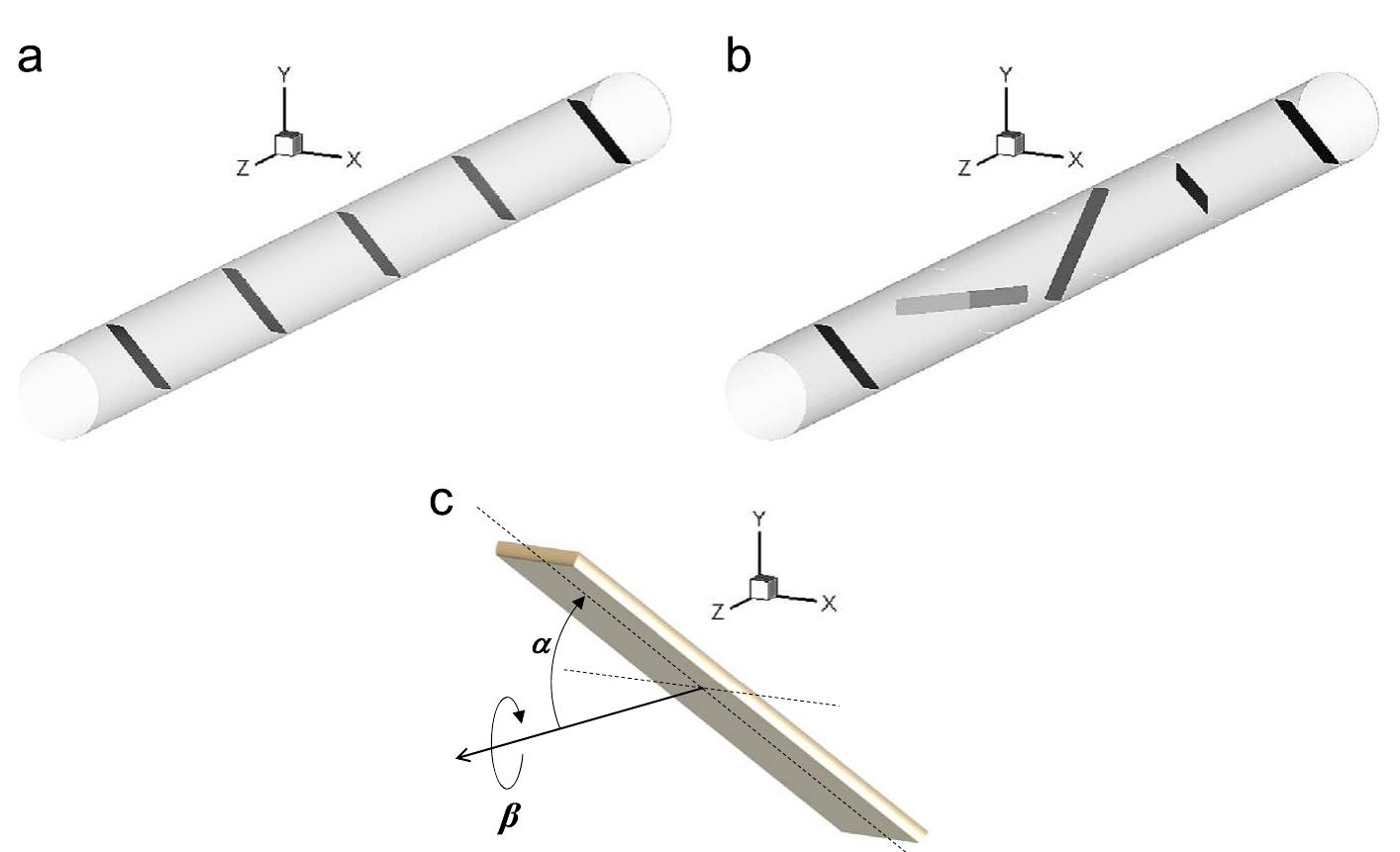
Fig. 1. Isometric views of the (a) in-line and (b) alternate configurations, and (c) of one tab with the main rotation angles. The flow is in the z-axis directio:
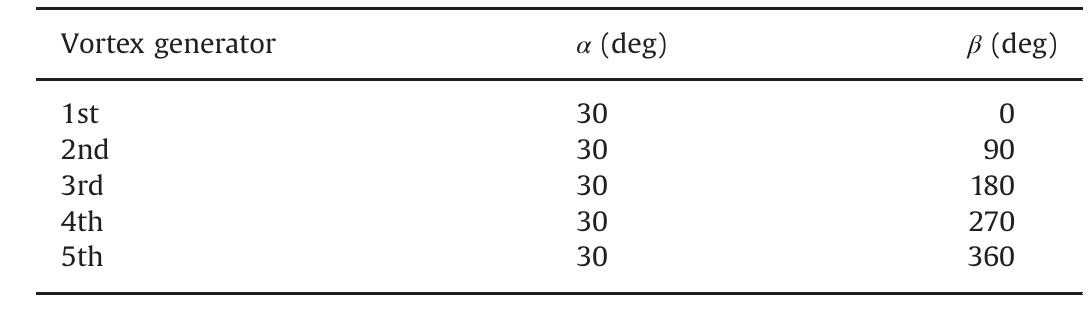
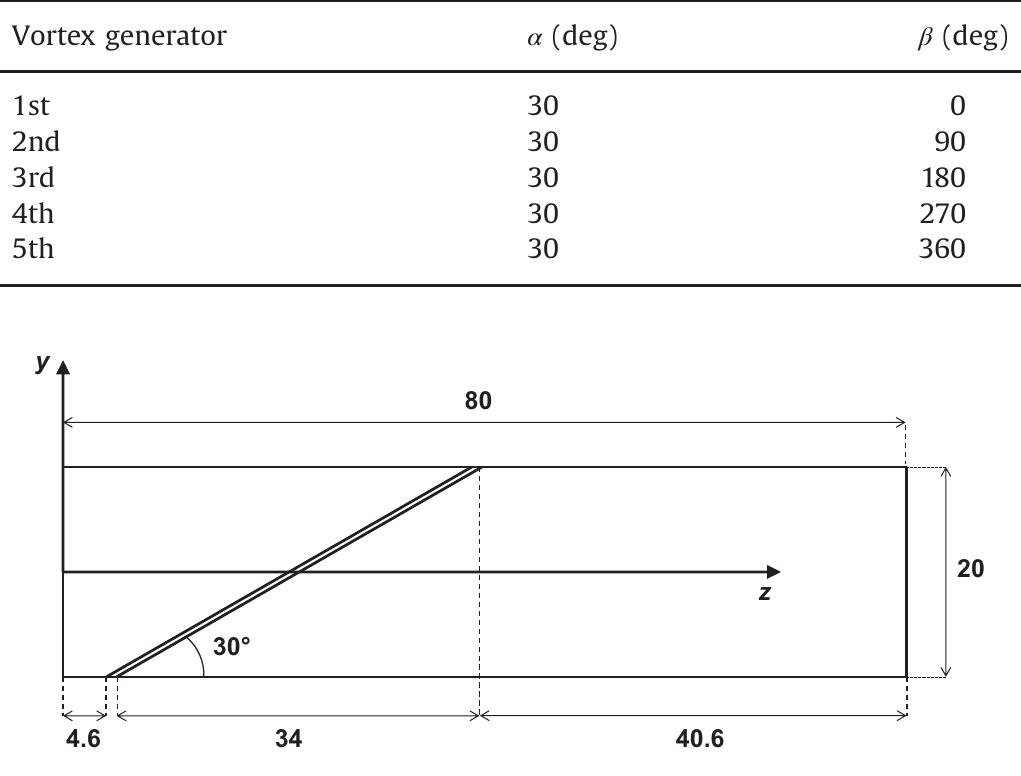
Fig. 2. Dimensions of a row of vortex generator (dimensions in mm). Transverse (a) and radial (#) angles of the vortex generators. Table 1
Fig. 3. Zoom on a single row of vortex generators showing the adapted mesh on (a) a cross-section (x, y) at Z=50 mm, (b) horizontal plane (x, z) and (c) vertical plane (y, z The Computational Fluid Dynamics CFD code Ansys Fluent is used for the present simulations. It is based on an Eulerian approach to solve Navier-Stokes equations through cell-centered finite volume discretization. The flow equations are solved sequen- tially with double precision and a second-order upwind scheme In fact, on ANSYS FLUENT, the iterations stop when all the criterions are achieved. Meanwhile, it is better to achieve a criterion of 10~® for the passive scalar equation to have an asymptotic behavior for T while this behavior is achieved at 10~° for the other equations.
Fig. 4. Streamwise vortex intensity and streamlines on cross-section (x, y) at different z (z in mm) for one row of vortex generato1
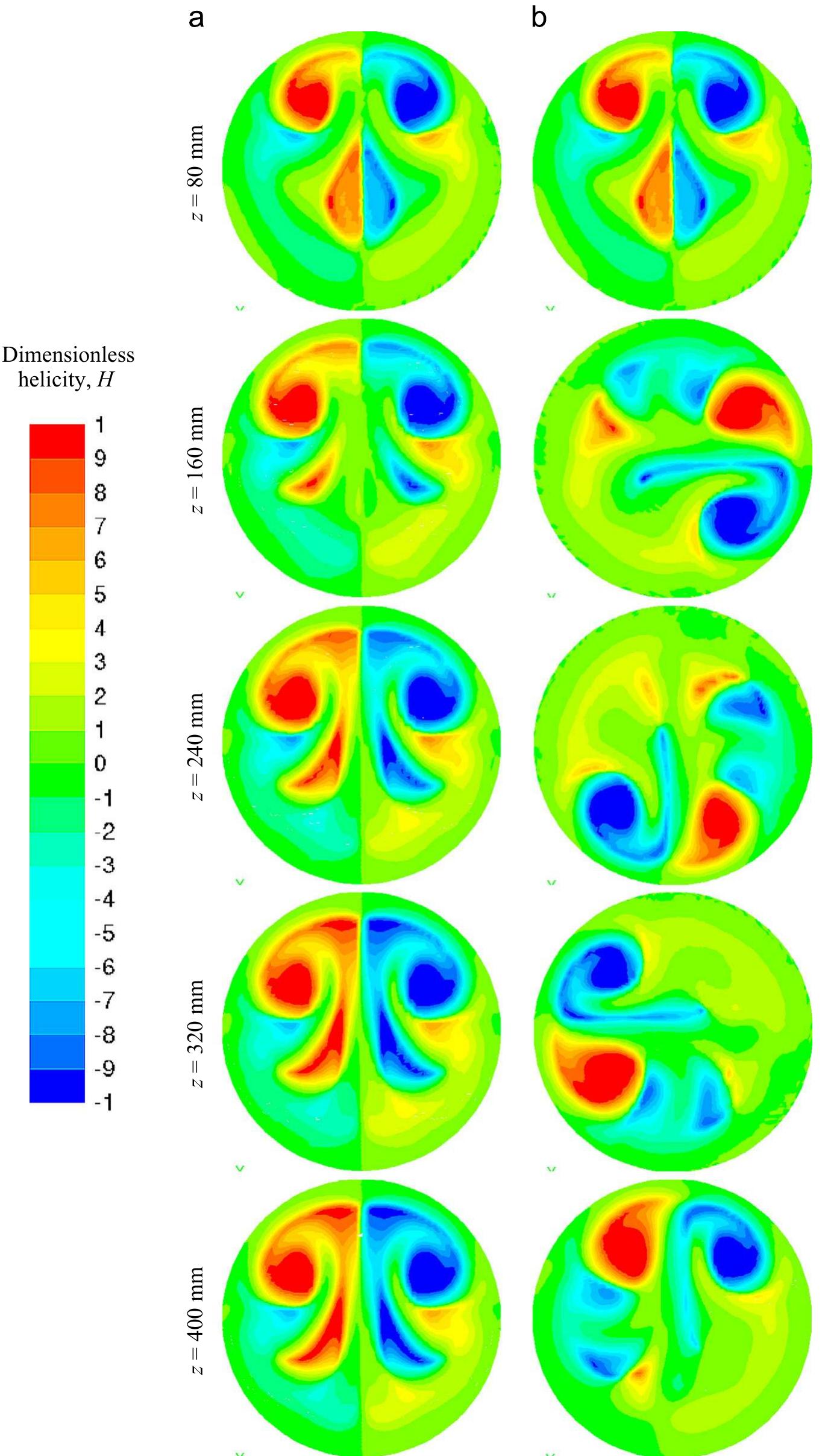
Fig. 5. Dimensionless helicity contours on different cross-sections for (a) in-line and (b) alternate configurations. A non-uniform unstructured three-dimensional mesh with hexahedral volumes is generated using Gambit software. Special Two flow configurations are studied; both consist of a circular pipe of radius r= 10 mm fitted by five rows of vortex generators. In the first configuration, as shown in Fig. l(a), the vortex generators are in-line in the flow direction, while in the second case, as shown in Fig. 1(b), an alternate radial rotation of 90° is applied on the angle / (Fig. 1(c)) which is presented by the values
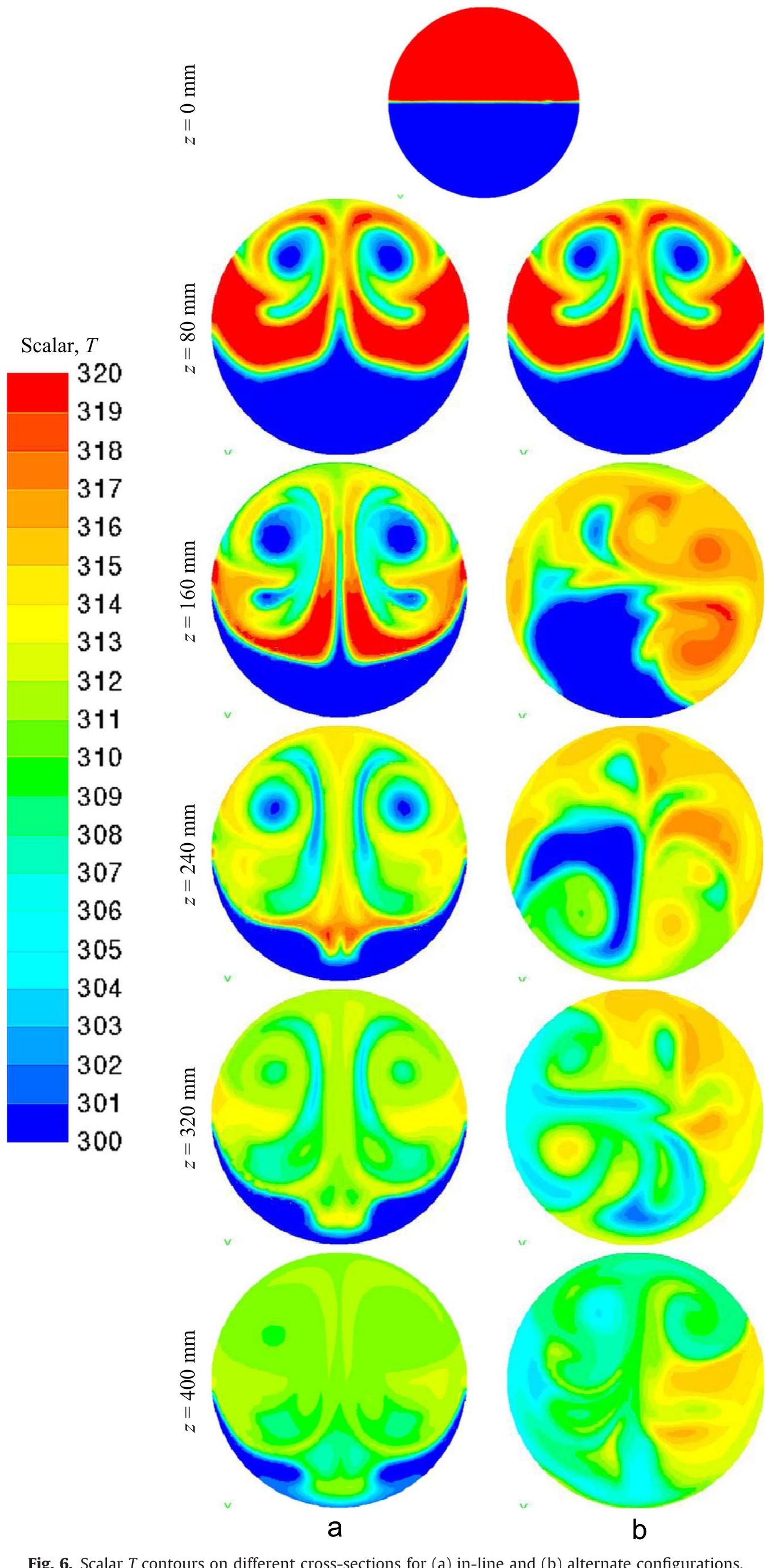
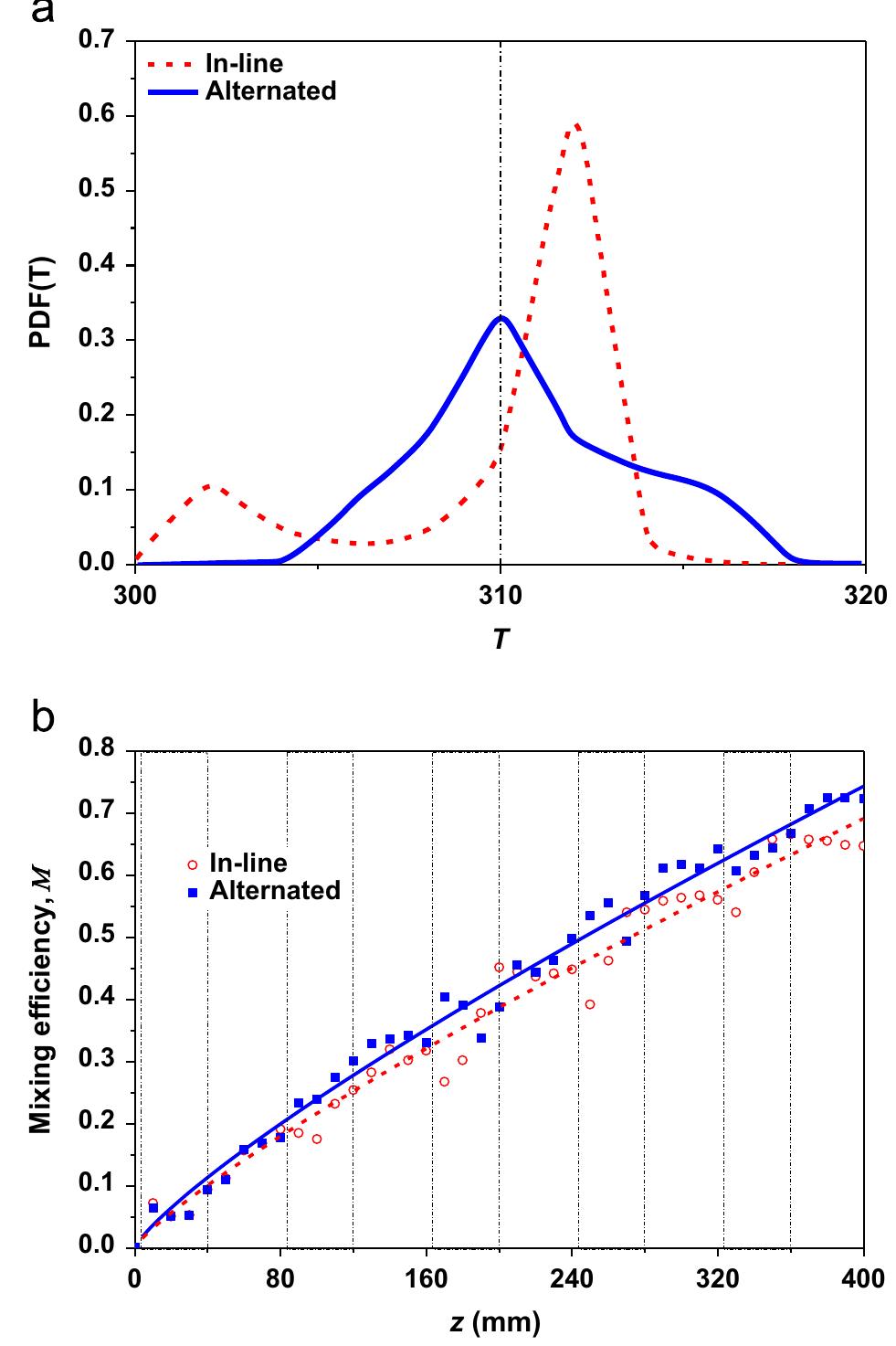
Fig. 7. (a) Probability density function at the MHER's outlet and (b) the evolution of the mixing fraction for both configurations. At the inlet (z =0 mm), as shown in Fig. 6, the upper region is set to Tmax =320 and in the lower region to Tin = 300. Fig. 6 shows the contours of the scalar T at the outlet of each of the five arrays for both cases. The strong effect of the primary CVP is
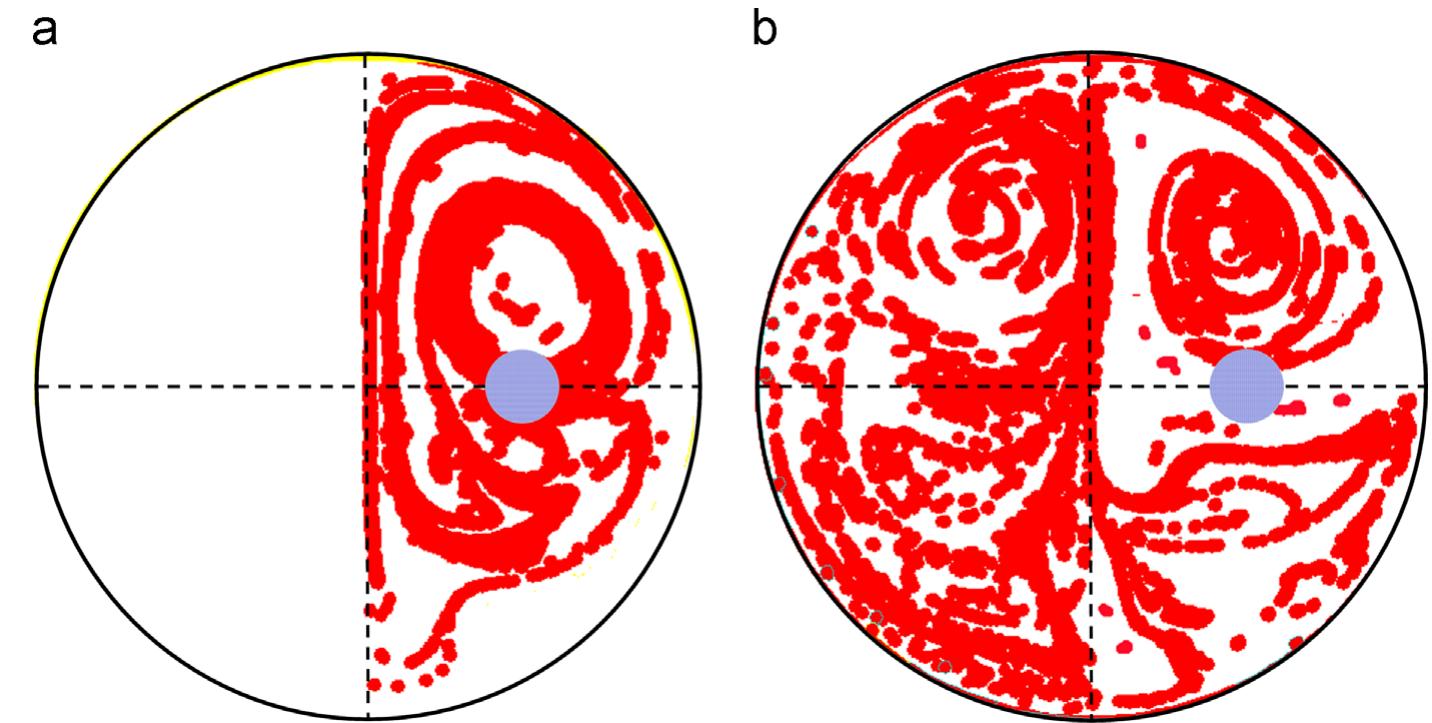
Fig. 8. Poincaré section for (a) in-line and (b) alternate configurations for initial 5000 particles injected at (xy9=5 mm, yo=0 mm). clearly highlighted by the distribution of the scalar especially for the first array. The engulfment process of Tyin into Tmax caused by the primary CVP shown in this Fig. 6 is very effective for the mixing process (Ottino, 1990; Hu et al., 2013). For the following arrays downstream, the scalar distribution in the in-line config- uration remains symmetrical and the engulfment process con- tinues similarly to the first array. However, it is intensified due to the fact that the primary CVP moves upward as it is shown in
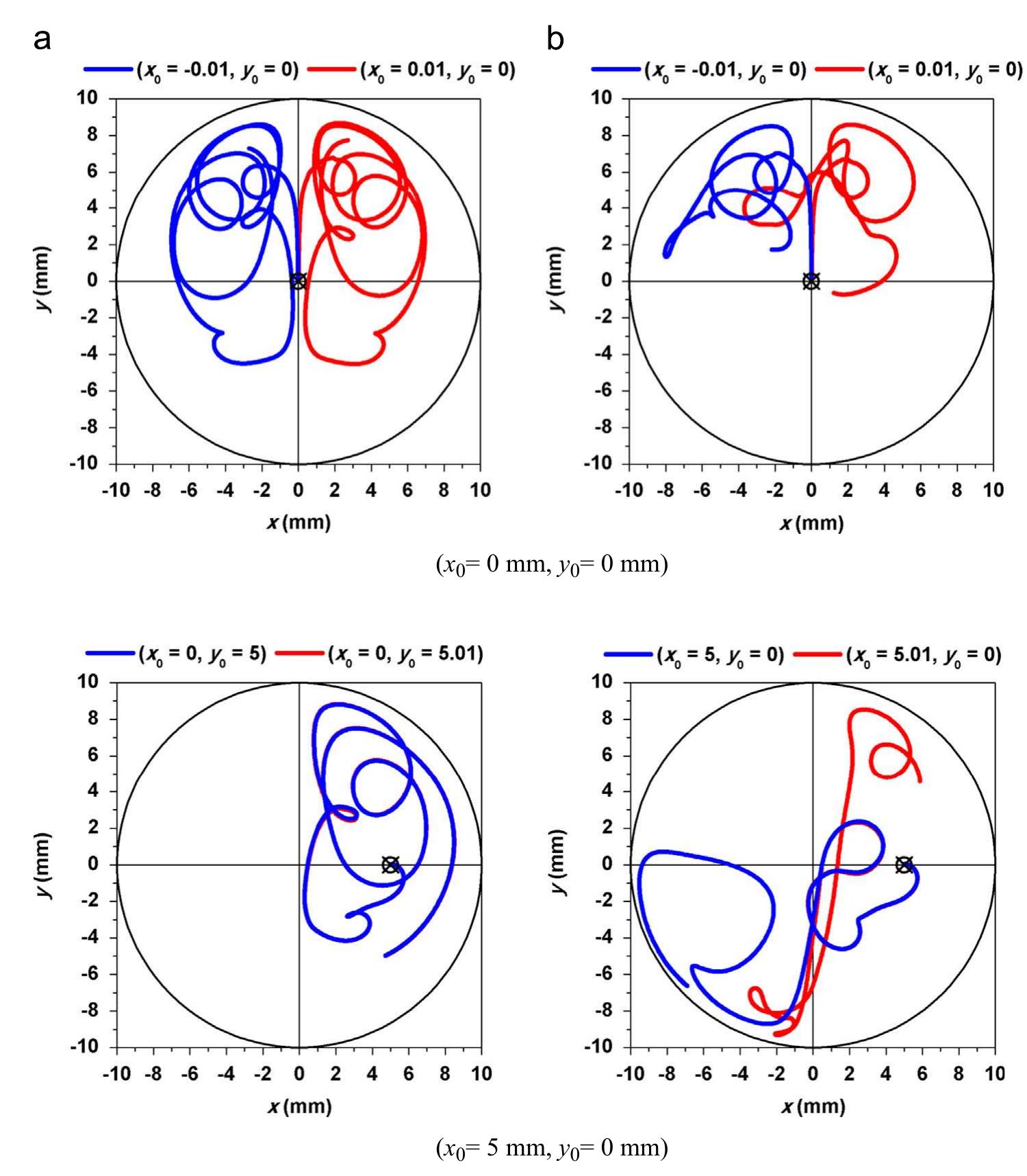
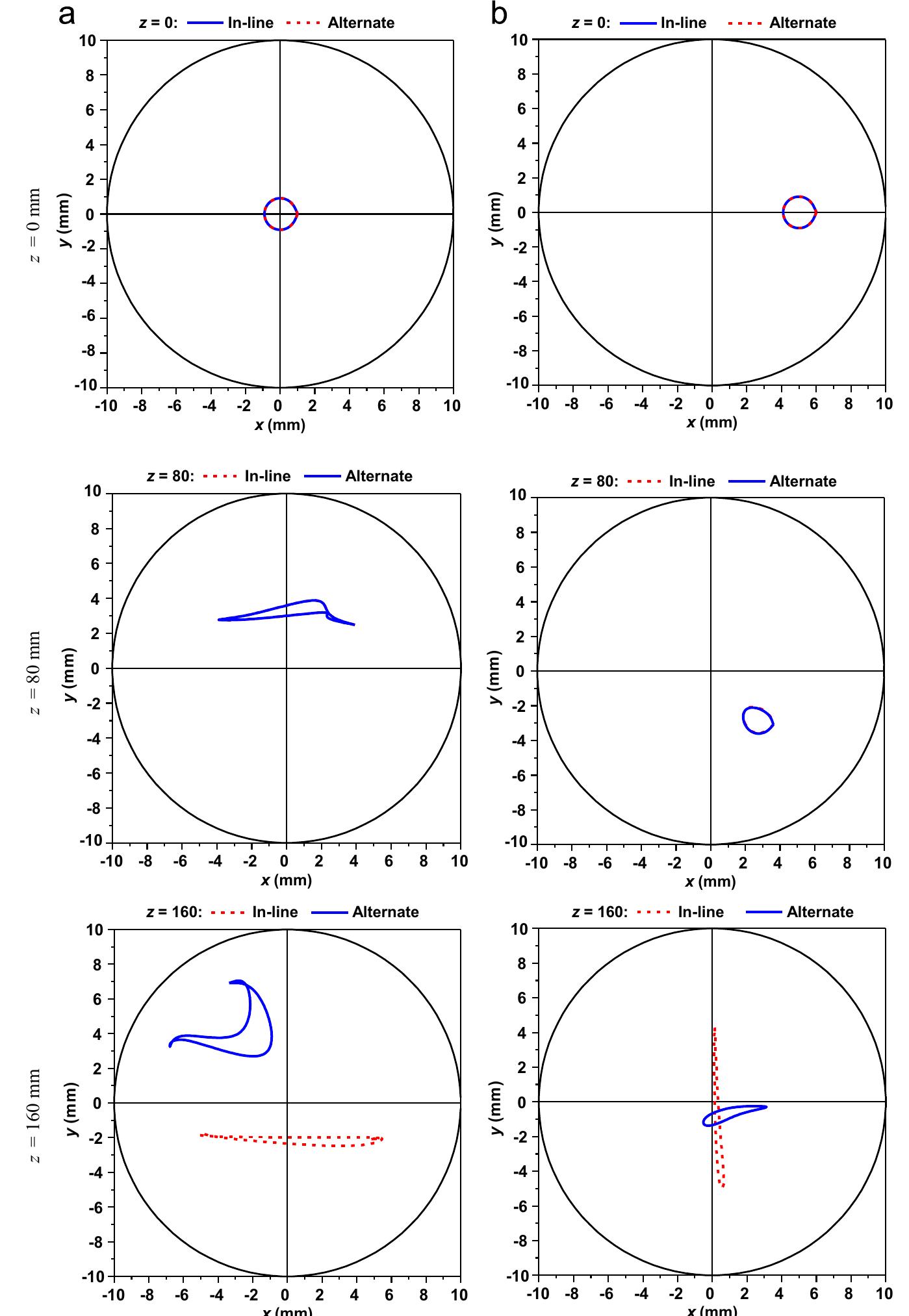
Fig. 9. Projections of the Lagrangian trajectories for different initial positions for the (a) in-line and (b) alternate configurations
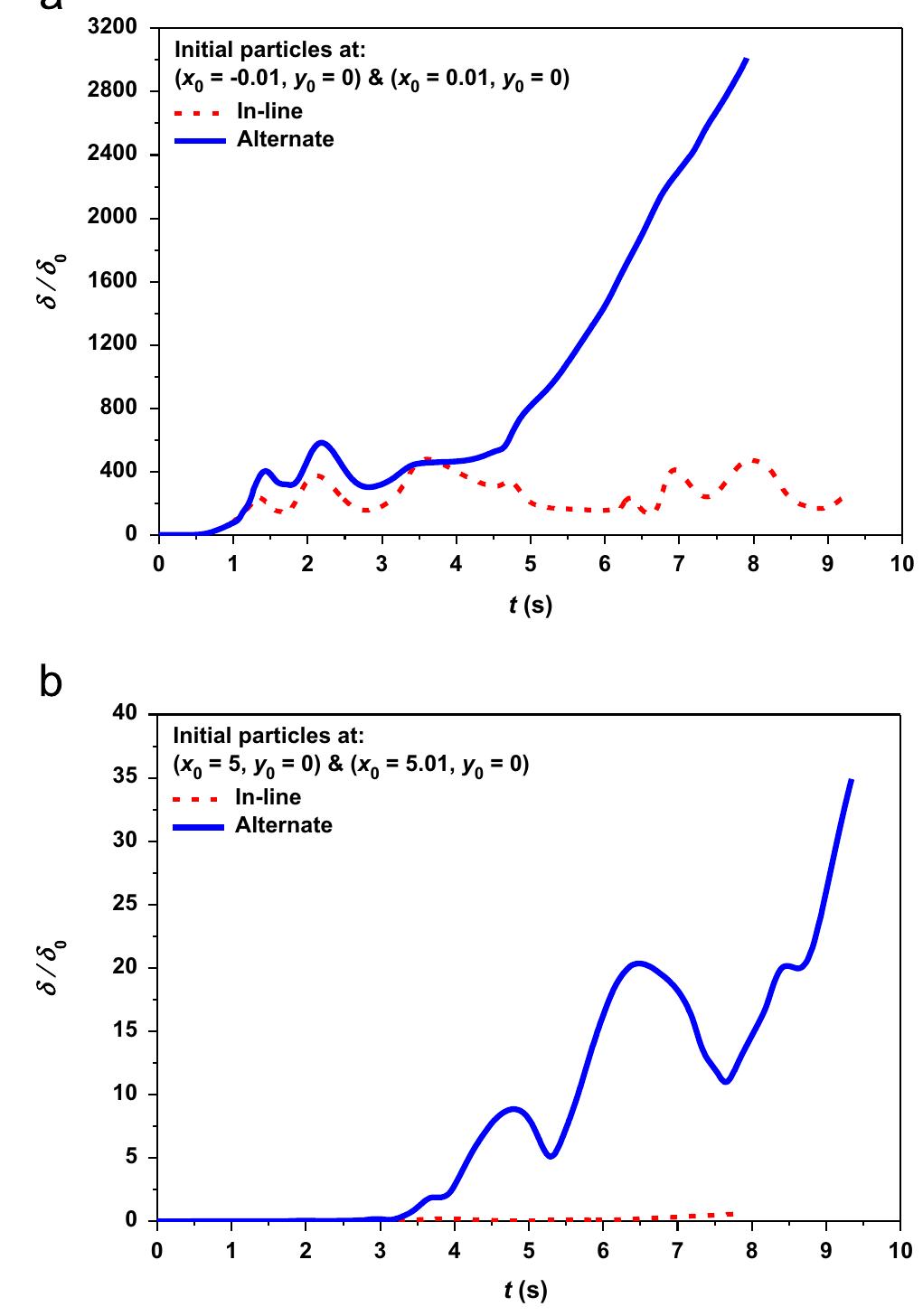
Fig. 10. Estrangement of two initially very close particles in both configurations. For the alternate configuration, the particles are found to move away from each other and the distance between them increases exponentially, while in the in-line configuration, the particles remain close. This exponential increase in the distance reported for the alternating configuration is caused by the chaotic advection flow.
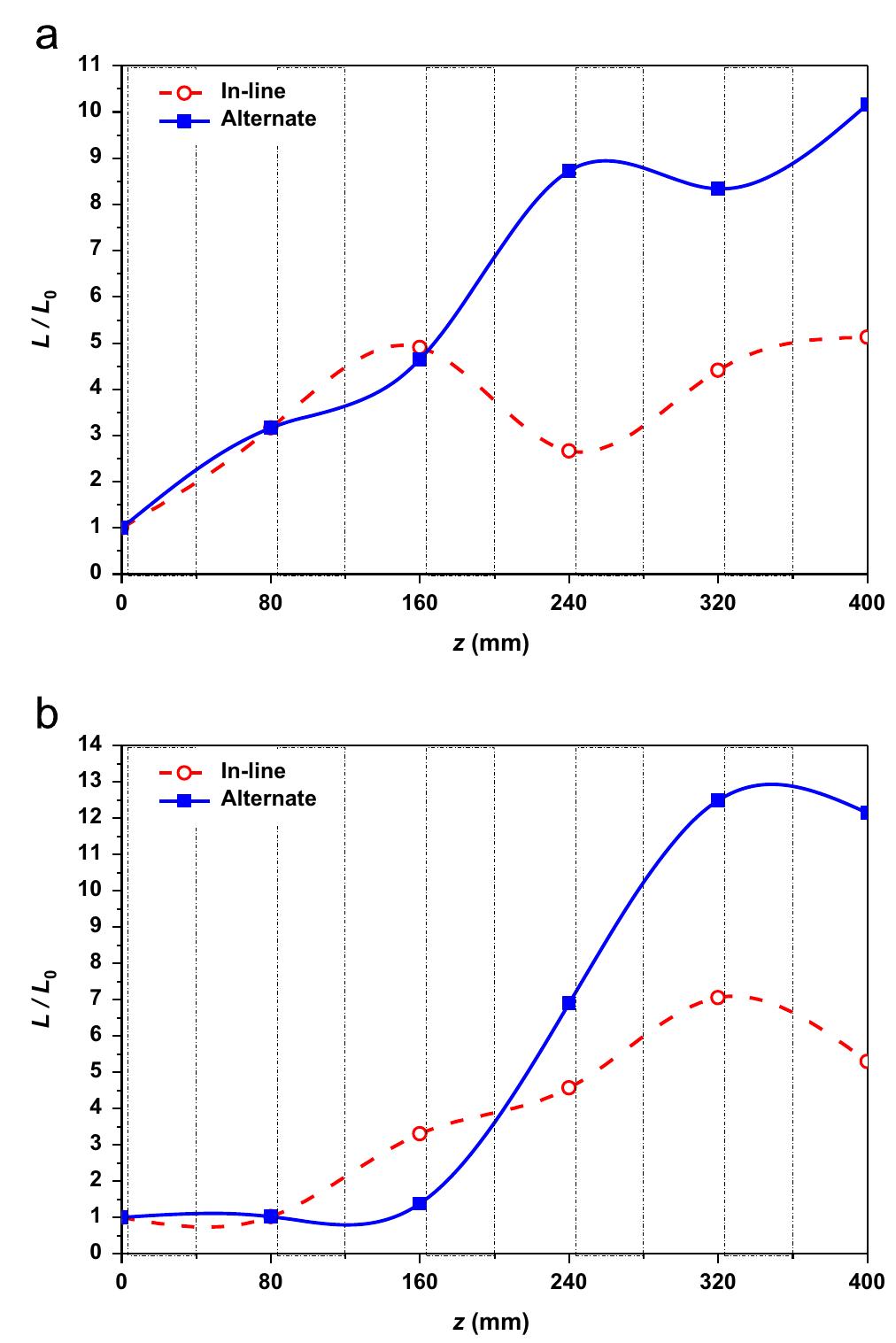
Fig. 11. Striation of initial circle of radius r=1 mm injected at the inlet and which is centered at (a) (¥g=0 mm, yo=O mm) and (b) (xo=5 mm, yo=0 mm) where py is the pressure at the inlet and p, is the average pressure in a given cross-section with the streamwise coordinate z. As it can be observed, when the particles pass throughout the different arrays of vortex generators, the stretching and folding of the circle become more significant, especially for the alternated case when irregular distributions are successively noticed in the flow direction. These random stretching and folding in the alternated configuration are very efficient for mixing different fluids or reagents (Ottino, 1989).
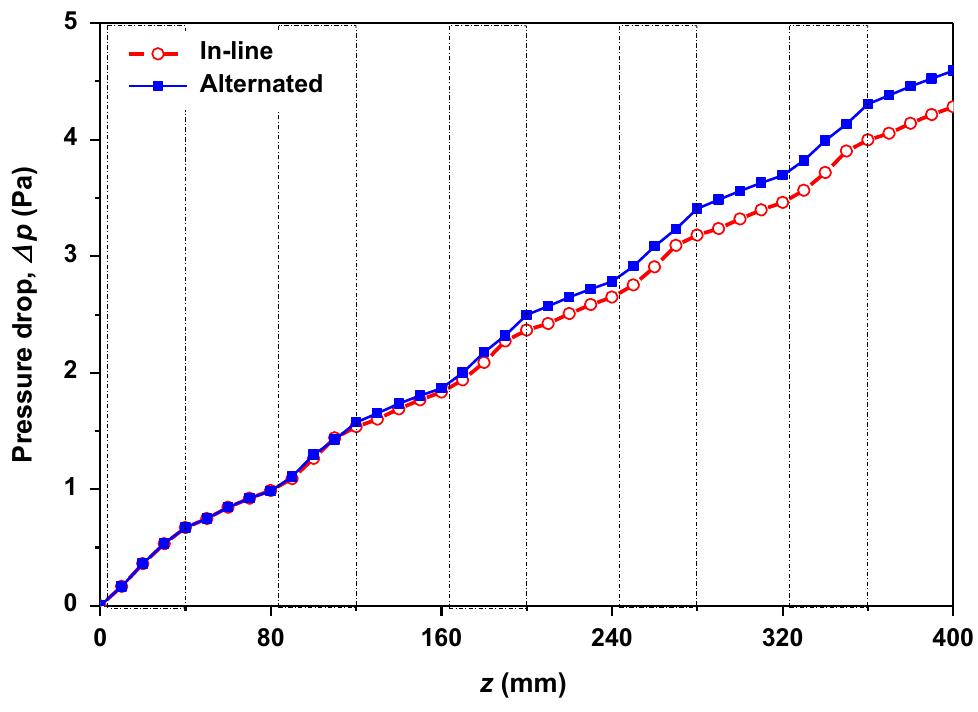
From this figure, it can be observed that Ap increases mono- lithically in both configurations. Downstream from the second vortex generator, the pressure drop in the alternate configuration becomes greater than that in the in-line one and reaches its maximum at the outlet. The maximum pressure drop increase in the alternate mixer does not exceed 7% relative to that in the in- line, while it was shown that the alternate configuration enhances the mixing efficiency by about 12% relative to that in the in-line configuration. This increase is caused by higher flow blockage area. mixing process within a multifunctional heat exchanger/reactor. Two configurations are studied; the first one consists of several arrays of rectangular vortex generators which are mounted in-line, while in the second one the arrays are periodically rotated by 90° with respect to the pipe axis. The flow is considered to be laminar and water is taken as the working fluid. As a first step, the flow structure is investigated showing that each vortex generator generates a counter-rotating streamwise vortex pair (CVP) which in its turn induces a secondary CVP in the very near-wall region. These CVPs are continuously rotated in the alternated configura- tion and cover a larger area in the flow volume. It is shown that the primary CVP is very efficient for the mixing process especially in the alternated configuration. However, the effect of the second- ary CVP on the mixing process is neglected. Moreover, by explor- ing the Poincaré sections and the Lagrangian trajectories of
Fig. 12. Striations length variation of initial circle of radius r= 1 mm injected at the inlet and which is centered at (a) (xy=0 mm, yo=0 mm) and (b) (xo=5 mm, yo=0 mm).
Fig. 13. Streamwise variation of the pressure drop for both configurations. different passive tracers, it is found that chaotic advection takes place in the alternated configuration while the flow in the in-line configuration stays regular. The future work will focus on different arrangements of the vortex generators arrays and on the effect of such geometries on the heat transfer in turbulent flow regimes.

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
References (34)
- Amon, C.H., Guzman, A.M., Morel, B., 1996. Lagrangian chaos, Eulerian chaos, and mixing enhancement in converging-diverging channel flow. Physics of Fluids 8, 1192-1206.
- Ansys Fluent. Academic Research. Release 14.0.
- Anxionnaz, Z., Cabassud, M., Gourdon, C., Tochon, P., 2008. Heat exchanger/reactors (HEX reactors): concepts, technologies: state-of-the-art. Chemical Engineering and Processing 47, 2029-2050.
- Aref, H., 1984. Stirring by chaotic advection. Journal of Fluid Mechanics 143, 1-21.
- Beuf, A., Gence, J.N., Carrière, P., Raynal, F., 2010. Chaotic mixing efficiency in different geometries of Hele-Shaw cells. International Journal of Heat and Mass Transfer 53, 684-693.
- Celik, I.B., Ghia, U., Roache, P.J., Freitas, C.J., Coleman, H., Raad, P.E., 2008. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. Journal of Fluids Engineering 130, 0780011-0780014.
- Chang, L.M., Wang, L.B., Song, K.W., Sun, D.L., Fan, J.F., 2009. Numerical study of the relationship between heat transfer enhancement and absolute vorticity flux along main flow direction in a channel formed by a flat tube bank fin with vortex generators. International Journal of Heat and Mass Transfer 52, 1794-1801.
- Dean, W.R., 1928. The streamline motion of fluid in curved pipe. Philosophical Magazine 5, 673-695.
- Fourcade, E., Wadley, R., Hoefsloot, H.C.J., Green, A., Iedema, P.D., 2001. CFD calculation of laminar striation thinning in static mixer reactors. Chemical Engineering Science 56, 6729-6741.
- Fourcade, E., Wadley, R., Hoefsloot, H.C.J., Green, A., Iedema, P.D., 2001. CFD calculation of laminar striation thinning in static mixer reactors. Chemical Engineering Science 56, 6729-6741.
- Habchi, C., Lemenand, T., Della Valle, D., Peerhossaini, H., 2009. Liquid/liquid dispersion in a chaotic advection flow. International Journal of Multiphase Flow 35, 485-497.
- Habchi, C., Lemenand, T., Della Valle, D., Peerhossaini, H., 2010. On the correlation between vorticity strength and convective heat transfer. In: Proceedings of the IHTC 14, ASME. vol. 2, pp. 377-382.
- Habchi, C., Lemenand, T., Della Valle, D., Pacheco, L., Le Corre, O., Peerhossaini, H., 2011. Entropy production and field synergy principle in turbulent vortical flows. International Journal of Thermal Sciences. 50, 2365-2376.
- Habchi, C., Russeil, S., Bougeard, D., Harion, J.L., Lemenand, T., Della Valle, D., Peerhossaini, H., 2012. Enhancing heat transfer in vortex generator-type multifunctional heat exchangers. Applied Thermal Engineering 38, 14-25.
- Hobbs, D.M., Muzzio, F.J., 1997. The Kenics static mixer: a three-dimensional chaotic flow. Chemical Engineering Journal 67, 153-166.
- Hu, W.L., Song, K.W., Guan, Y., Chang, L.M., Liu, S., Wang, L.B., 2013. Secondary flow intensity determines Nusselt number on the fin surfaces of circle tube bank fin heat exchanger. International Journal of Heat and Mass Transfer 62, 620-631.
- Jones, S.W., Thomas, O.M., Aref, H., 1989. Chaotic advection by laminar flow in a twisted pipe. Journal of Fluid Mechanics 209, 335-357.
- Lambert, R.A., Rangela, R.H., 2010. The role of elastic flap deformation on fluid mixing in a microchannel. Physics of Fluids 22, 052003.
- Le Guer, Y., El Omari, K., 2012. Chaotic advection for thermal mixing. Advances in Applied Mechanics 45, 189-237.
- Le Guer, Y., Peerhossaini, H., 1991. Order breaking in Dean flow. Physics of Fluids 3, 1029-1032.
- Mardaru, A., Souidi, K., Marcati, A., Jinescu, G., Habchi, C., Della Valle, D., Djelveh, G., 2012. Effect of impellers configuration on the gas dispersion of high-viscosity fluid using Narrow Annular Gap Unit. Part 2: numerical approach. Chemical Engineering Science 75, 63-74.
- Ottino, J.M., 1989. The Kinematics of Stretching, Chaos and Transport. Cambridge University Press, Cambridge, UK.
- Ottino, J.M., 1990. Mixing, chaotic advection, and turbulence. Annual Review in Fluid Mechanics 22, 207-253.
- Pai, S.A., Prakash, P., Patnaik, P.S.V., 2013. Numerical simulation of chaotic mixing in lid-driven cavity: effect of passive plug. Engineering Applications of Computa- tional Fluid Mechanics 7, 406-418.
- Patankar, S., 1980. Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Co., New York, pp. 330-351.
- Phillips, C.H., Lauschke, G., Peerhossaini, H., 1997. Intensification of batch chemical processes by using integrated chemical reactor-heat exchangers. Applied Thermal Engineering 17, 809-824.
- Rauline, D., Tanguy, P.A., Le Blevec, Bousquet, J., 1998. Numerical investigation of the performance of several static mixers. Canadian Journal of Chemical Engineering 76, 527-535.
- Saatdjian, E., Rodrigo, A.J.S., Mota, J.P.B., 2012. A study of mixing by chaotic advection in two three-dimensional open flows. Chemical Engineering Science 81, 179-190.
- Southerland, K.B., Frederiksen, R.D., Dahm, W.J.A., Dowling, D.R., 1994. Comparisons of mixing in chaotic and turbulent flows. Chaos, Solitons and Fractals 4, 1057-1089.
- Stankiewicz, A., Moulijn, J., 2000. Process intensification: transforming chemical engineering. Chemical Engineering Progress 96, 22-34.
- Thakur, R.K., Vial, Ch., Nigam, K.D.P., Nauman, E.B., Djelveh, G., 2003. Static mixers in the process industries-a review. Chemical Engineering Research and Design 81, 787-826.
- Timité, B., Castelain, C., Peerhossaini, H., 2011. Mass transfer and mixing by pulsatile three-dimensional chaotic flow in alternating curved pipes. International Journal of Heat and Mass Transfer 54, 3933-3950.
- Warming, R.F., Beam, R.M., 1976. Upwind second-order difference schemes and applications in aerodynamic flows. AIAA Journal 14, 1241-1249.
- Wiggins, S., Ottino, J.M., 2004. Foundations of chaotic mixing. Philosophical Transaction of the Royale Society of London A 362, 937-970.