Informational complexity criteria for regression models (original) (raw)

Abstract

This paper pursues three objectives in the context of multiple regression models: • To give a rationale for model selection criteria which combine a badness-of-fit term (such as minus twice the maximum log likelihood) with a measure of complexity of a model. We show that the ICOMP criterion introduced by Bozdogan can be seen as an approximation to the sum of two Kullback-Leibler distances, and that a criterion related to ICOMP arises as an approximation to the posterior expectation of a certain utility.

Figures (9)

Remark. If the matrix X’X is diagonal, as is the case for orthogonal designs, and if the columns of X are scaled so as to have the same norm, then the complexity of (X'X)~' is zero. So in the definition of JCOMP,,, suitably scaled designs will have zero complexity. This is not the case in the definition of JCOMPIFIM. Therefore, if all models under consideration are orthogonal designs, JCOMPIFIM might be preferable.

Remark. If the matrix X’X is diagonal, as is the case for orthogonal designs, and if the columns of X are scaled so as to have the same norm, then the complexity of (X'X)~' is zero. So in the definition of JCOMP,,, suitably scaled designs will have zero complexity. This is not the case in the definition of JCOMPIFIM. Therefore, if all models under consideration are orthogonal designs, JCOMPIFIM might be preferable.

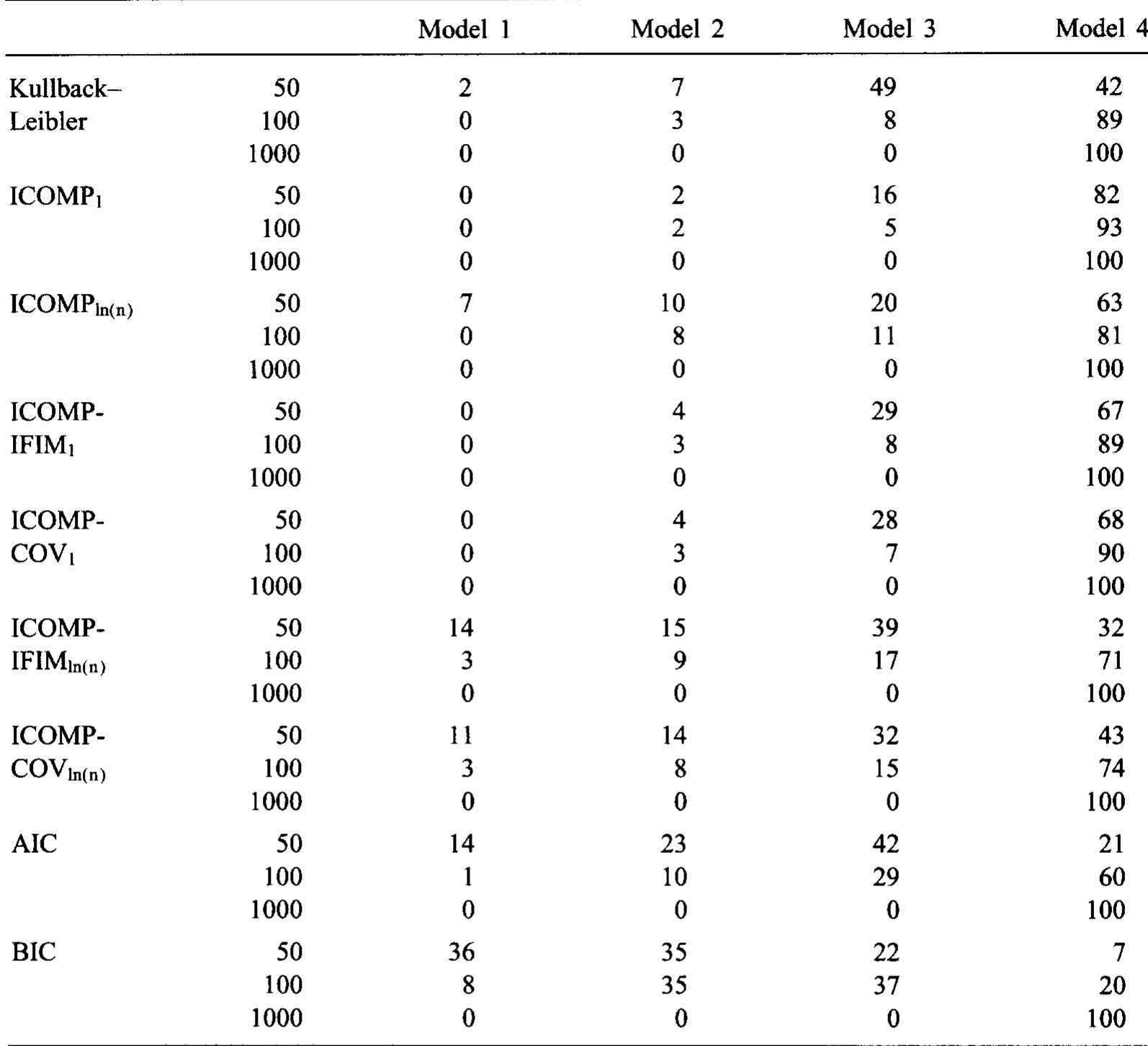
Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o* = 5; 8 = Bmax; sample sizes of 50,100,1000 Note: The value of Bmax for the parameter vector B gives maximum variability to XB. The values of Bmax are as follows for each sample size: Table la

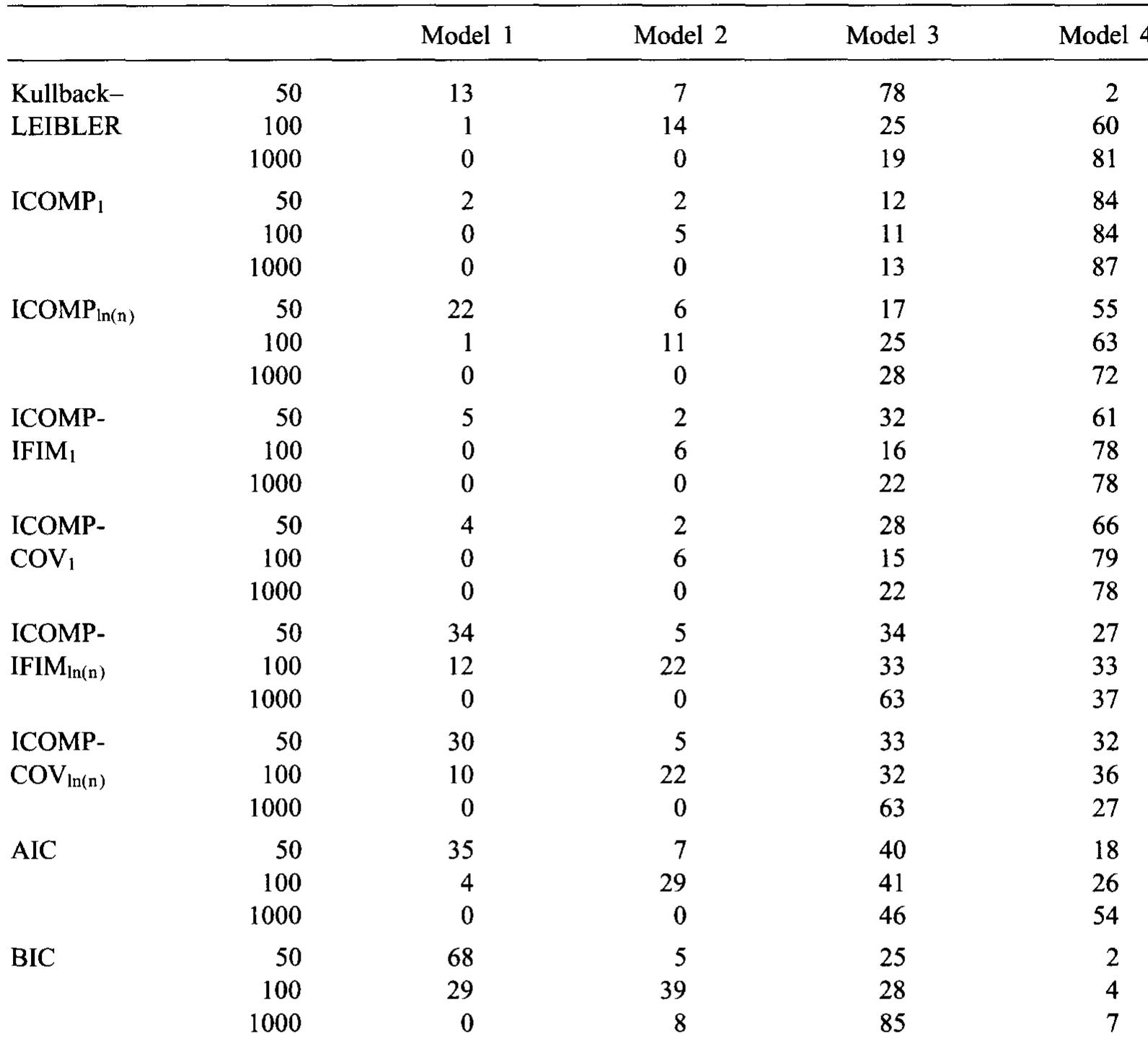
Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o* = 5; 8 = Bmax; sample sizes of 50,100,1000 Note: The value of Bmax for the parameter vector B gives maximum variability to XB. The values of Bmax are as follows for each sample size: Table la

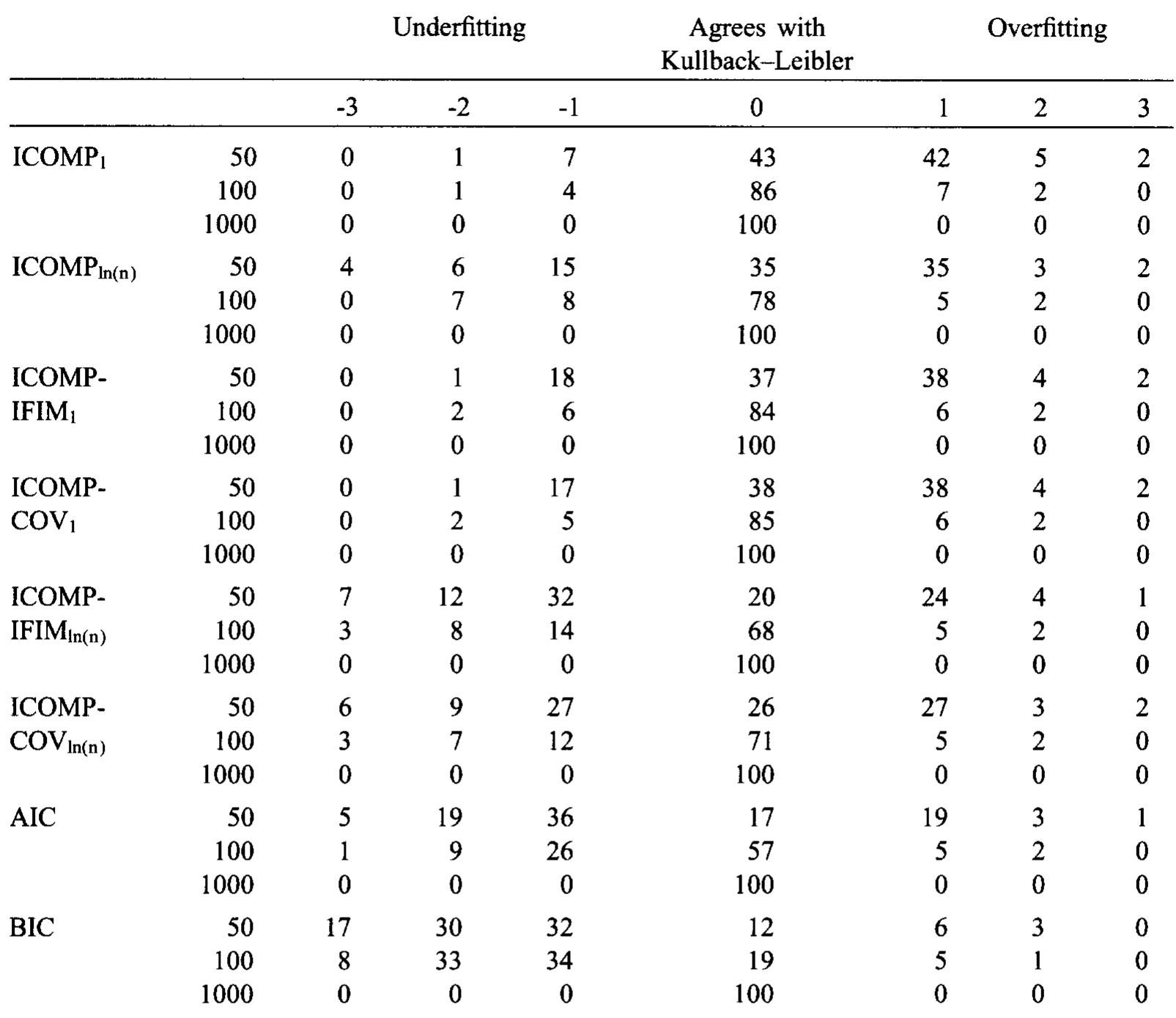
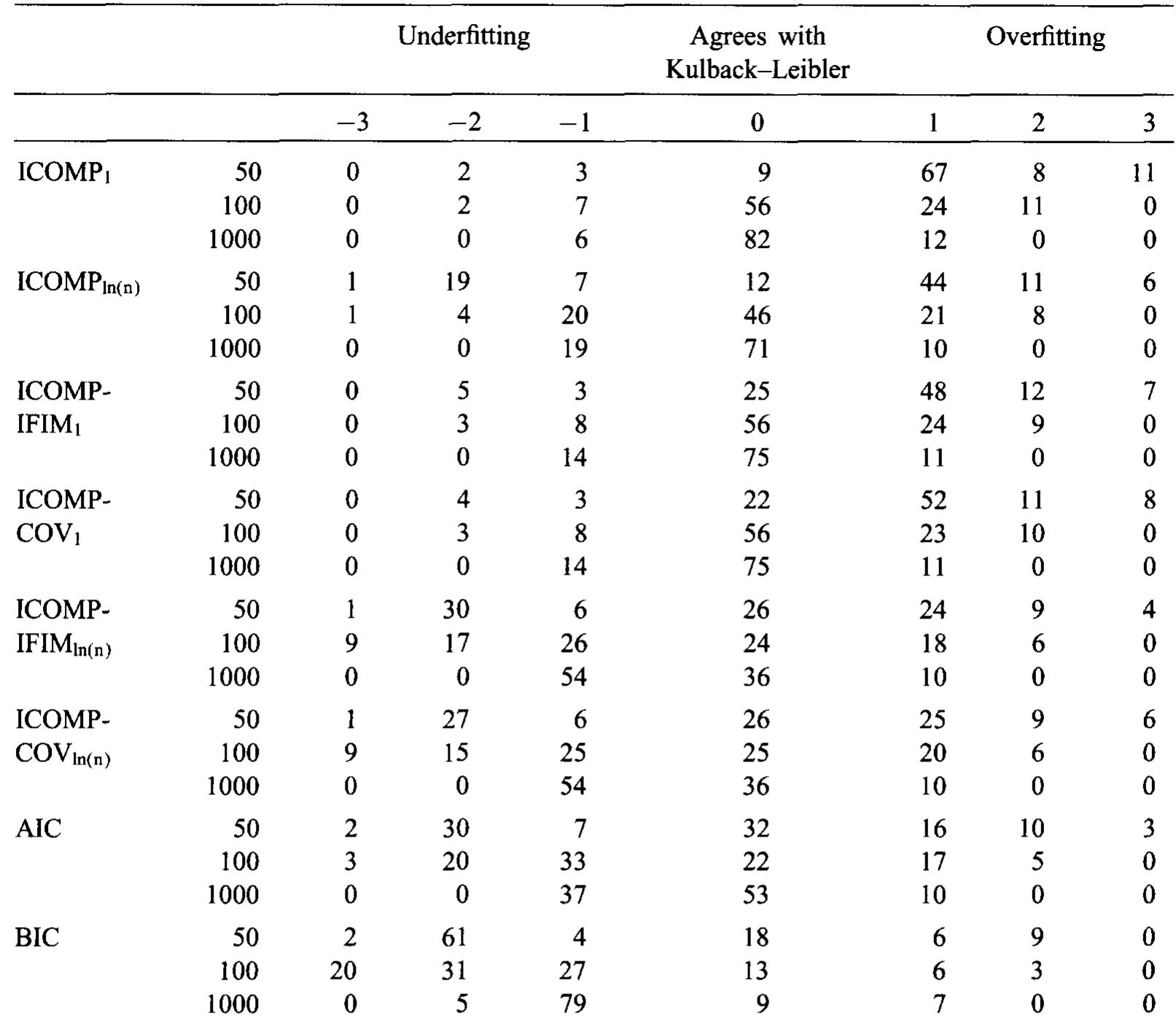
Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; o? = 5; B = Bmax; Sample sizes of 50,100,1000 Note: The value of Bmax for the parameter vector B gives maximum variability to XB. The values of Bmax are as follows for each sample size:

Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; o? = 5; B = Bmax; Sample sizes of 50,100,1000 Note: The value of Bmax for the parameter vector B gives maximum variability to XB. The values of Bmax are as follows for each sample size:

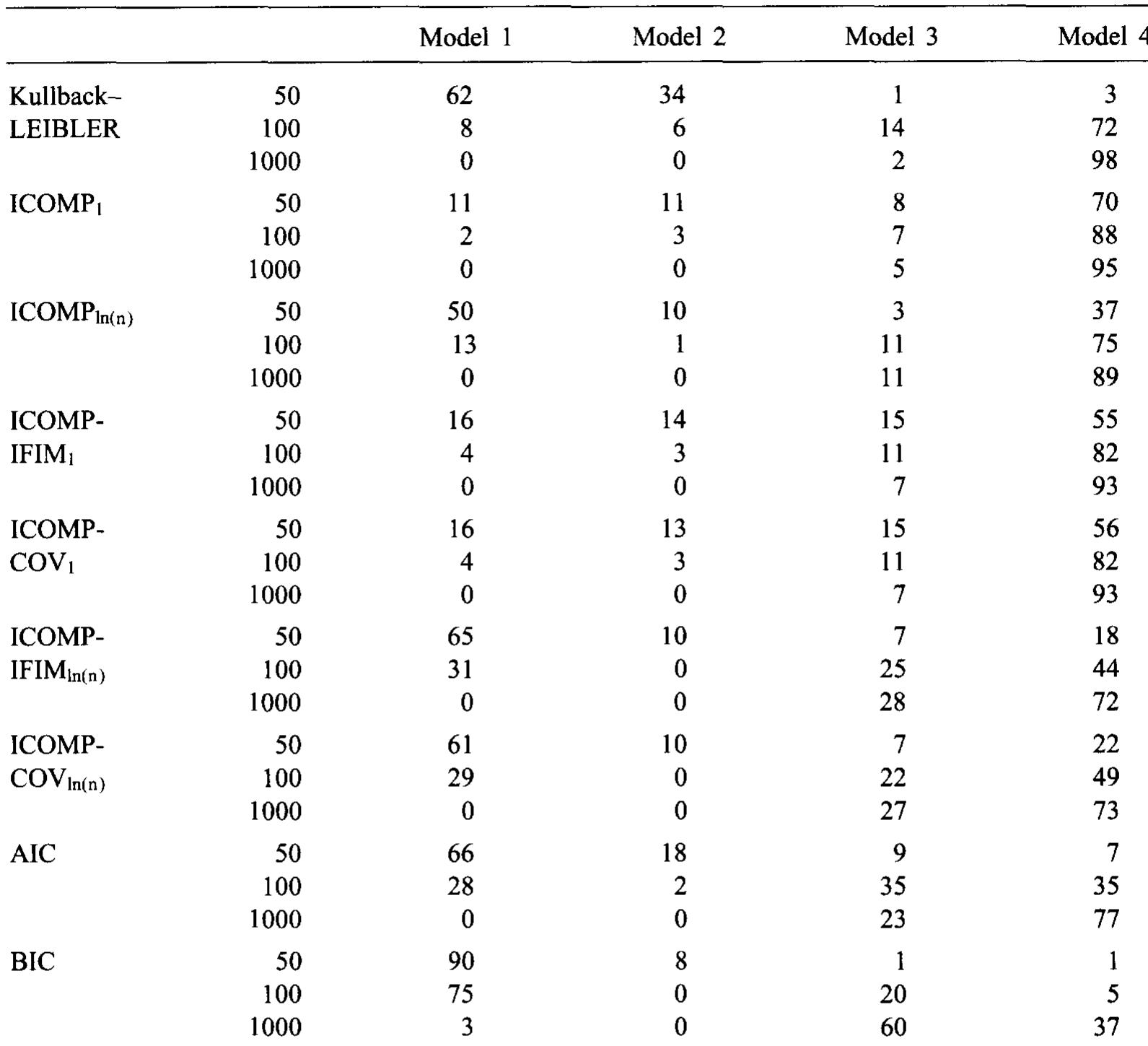
Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o? = 5; B = Bin; sample sizes of 50,100,1000 Note: The value of fin for the parameter vector f is the average of Bmax and Pmin. The values of Pint are as follows for each sample size: Table 2a

Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o? = 5; B = Bin; sample sizes of 50,100,1000 Note: The value of fin for the parameter vector f is the average of Bmax and Pmin. The values of Pint are as follows for each sample size: Table 2a

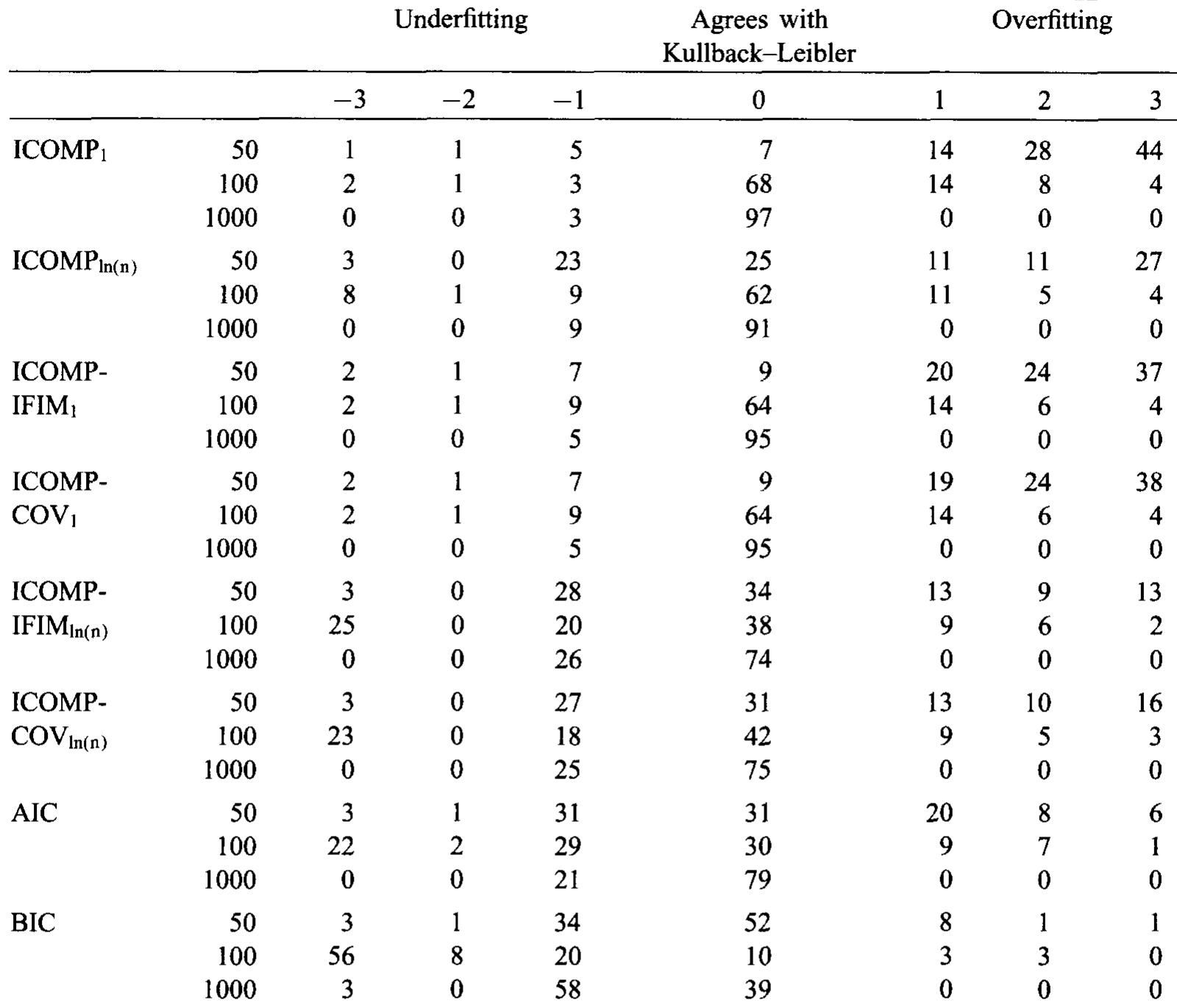
Differences between the dimensions of models selected by each criterion and by the Kulback~Leibler distance for 100 replicates; o? = 5; 8 = Bim; Sample sizes of 50,100,1000 Note: The value of fin for the parameter vector f is the average of Bmax and Bmin. The values of Pin are as follows for each sample size:

Differences between the dimensions of models selected by each criterion and by the Kulback~Leibler distance for 100 replicates; o? = 5; 8 = Bim; Sample sizes of 50,100,1000 Note: The value of fin for the parameter vector f is the average of Bmax and Bmin. The values of Pin are as follows for each sample size:

Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o* = 5; 8 = Bmin; sample sizes of 50,100,1000 Note: The value of Bmin for the parameter vector 8 gives minimum variability to X8. The values of Amin are as follows for each sample size: Table 3a

Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 100 replicates; o* = 5; 8 = Bmin; sample sizes of 50,100,1000 Note: The value of Bmin for the parameter vector 8 gives minimum variability to X8. The values of Amin are as follows for each sample size: Table 3a

Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; 0? = 5; B = Bmin; sample sizes of 50,100,1000 Note: The value of Bmin for the parameter vector 8 gives minimum variability to Xf. The values of Bmin are as follows for each sample size:

Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; 0? = 5; B = Bmin; sample sizes of 50,100,1000 Note: The value of Bmin for the parameter vector 8 gives minimum variability to Xf. The values of Bmin are as follows for each sample size:

Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 10 replicates; o? = .25; sample size = 50; Extreme and intermediate values of B Note: The value of Bmax for the parameter vector B gives maximum variability to Xf, and the value of Bmin for the parameter vector B gives minimum variability to Xf. The value of fim for the parameter B is the average of Bmax and Bmin. See Tables 1A, 1B, 2A, 2B, 3A, 3B for the numerical values of Bmax, Bint and Buin.

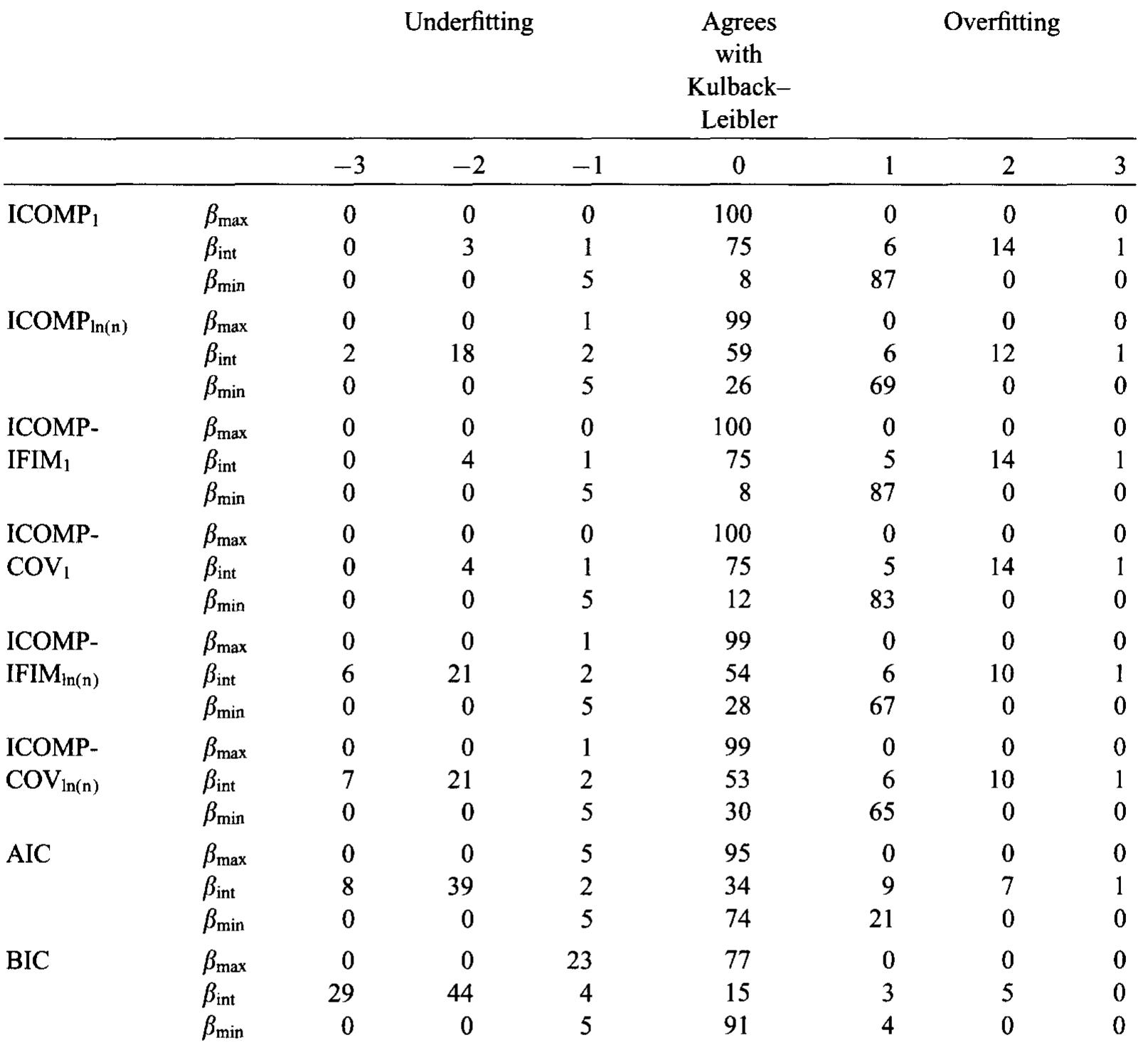
Frequency of selections of models 1-4 by each criterion and the Kullback—Leibler distance for 10 replicates; o? = .25; sample size = 50; Extreme and intermediate values of B Note: The value of Bmax for the parameter vector B gives maximum variability to Xf, and the value of Bmin for the parameter vector B gives minimum variability to Xf. The value of fim for the parameter B is the average of Bmax and Bmin. See Tables 1A, 1B, 2A, 2B, 3A, 3B for the numerical values of Bmax, Bint and Buin.

Note: The value of Bmax for the parameter vector Bf gives maximum variability to Xf, and the value of Bmin for the parameter vector 8 gives minimum variability to Xf. The value of fin for the parameter B is the average of Bmax and Bmin. See Tables 1A, 1B, 2A, 2B, 3A, 3B for the numerical values of Bmax; Bint and Brin. Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; o? = .25; sample size = 50; Extreme and intermediate values of B

Note: The value of Bmax for the parameter vector Bf gives maximum variability to Xf, and the value of Bmin for the parameter vector 8 gives minimum variability to Xf. The value of fin for the parameter B is the average of Bmax and Bmin. See Tables 1A, 1B, 2A, 2B, 3A, 3B for the numerical values of Bmax; Bint and Brin. Differences between the dimensions of models selected by each criterion and by the Kullback—Leibler distance for 100 replicates; o? = .25; sample size = 50; Extreme and intermediate values of B

Loading...

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

References (31)

  1. Akaike, H., 1973. Information theory and an extension of the maximum likelihood principle. In B.N. Petrov and F. Cz/lki, (Eds.), 2nd Intrnat. Symp. on Information Theory, Akademiai Kiad6, Budapest, pp. 267-281.
  2. Bearse, P.M., Bozdogan, H., Schlottmann A., 1997. Empirical econometric modelling of food consumption using a new informational complexity approach. J. Appl. Econometrics, 12, 563-592.
  3. Bozdogan, H., 1987. Model selection and Akaike's information criterion (AIC): The general theory and its analytical extensions, Psychometrika, 52 (3) Special Section (invited paper), 345-370.
  4. Bozdogan, H., 1988. ICOMP: A new model selection criterion. In: H.H. Bock (Ed.), Classification and Related Methods of Data Analysis, North-Holland, Amsterdam, 599-608.
  5. Bozdogan, H., 1990. On the information-based measure of covariance complexity and its application on the evaluation of multivariate linear models. Commun. Statist. Theory Methods, 19 (1), 221-278.
  6. Bozdogan, H., 1993. Choosing the number of component clusters in the mixture model using a new informational complexity criterion of the inverse Fisher information matrix. In: O. Opitz, B. Lausen, and R. Klar (Eds.), Studies in Classification, Data Analysis, and Knowledge Organization, Springer, Heidelberg, pp. 40-54.
  7. Bozdogan, H., 1994. Mixture-model cluster analysis using a new informational complexity and model selection criteria. In: H. Bozdogan (Ed.), Multivariate Statistical Modeling, vol. 2, Proc. 1st US/Japan Conference on the Frontiers of Statistical Modeling: An Informational Approach, Kluwer Academic Publishers, the Netherlands, Dordrecht, pp. 69-113.
  8. Bozdogan, H., 1995a. Statistical modeling and model evaluation: a new informational approach. A forthcoming book.
  9. Bozdogan, H., 1995b. Informational statistical modeling with MATLAB: a user's guide and handbook, forthcoming.
  10. Bozdogan, H., 1998. Akaike information criteria and recent developments in informational complexity. Invited paper to appear in: J. Math. Psychology.
  11. Chalton, D.O., 1990. Contributions to influence, outliers, and Bayesian analysis in the multiple regression model. Unpublished Ph.D. Thesis, the Department of Mathematical Statistics, University of Cape Town, Cape Town, South Africa.
  12. Haughton, D., 1988. On the choice of a model to fit data from an exponential family. Ann. Statist. 16, 342-355.
  13. Haughton, D., 1990. Size of the error in the choice of a model to fit data from an exponential family. Sankhy~ A, 51, 45-58.
  14. Haughton, D., 1991. Consistency of a class of information criteria for model selection in non-linear regression, Commun. Statist. Theory Methods, 20, 1619-1629.
  15. Hoffman, K., R., Kunze, 1971. Linear Algebra. Prentice-Hall, Englewood Cliffs, NJ.
  16. Johnson, R.A., Wichern, D.W., 1992. Applied Multivariate Statistical Analysis, 3rd ed. Prentice-Hall, Englewood Cliffs, NJ.
  17. Kass, R.E., Tierney, L., Kadane, J.B., 1990. The validity of posterior expansions based on Laplace's method. In: Geisser, S., Hodges, J.S., Press, S.J., Zellner, A. (Eds.), Bayesian and Likelihood Methods in Statistics and Econometrics. North-Holland, Amsterdam, pp. 473-488.
  18. Kullback, S., Leibler, R., 1951. On information and sufficiency. Ann. Math. Statist., 22, 79-86.
  19. Magnus, J., Neudecker, H., 1988. Matrix Differential Calculus with Applications in Statistics and Econometrics. Wiley, New York.
  20. McDonald, G.C., Galarneau, D.I., 1975. A Monte Carlo evaluation of some ridge-type estimators. J. Amer. Statist. 70, 407-416.
  21. Nishii, R., 1984. Asymptotic properties of criteria for selection of variables in multiple regression. Ann. Statist. 12, 758-765.
  22. Poskitt, D.S., 1987. Precision, complexity and Bayesian model determination. J. Roy. Statist. Soc. 49, 199-208.
  23. Prtscher, B.M. 1989. Model selection under nonstationarity: autoregressive models and stochastic linear regression models. Ann. Statist. 17, 1257-1274.
  24. Sakamoto, Y., Ishiguro, M., Kitagawa, G., 1986. Akaike Information Criterion Statistics. KTK Scientific Publishers, Tokyo.
  25. Schwarz, G., 1978. Estimating the dimension of a model. Ann. Statist. 6, 461-464.
  26. Searle, S.R., 1971. Linear Models. Wiley, New York.
  27. Shao, J., 1993. Linear model selection by cross-validation. J. Amer. Statist. Assoc. 88, 486-494.
  28. Stewart, J., 1991. Econometrics. Philip Allan, New York.
  29. Stone, M., 1977. An asymptotic equivalence of choice of model by cross-validation and Akaike's criterion. J. Roy. Statist. Soc. B, 39, 44~7.
  30. van Emden, M., 1971. An analysis of complexity. Mathematisch Centrum Tracts 35, Mathematisch Centrum, Amsterdam.
  31. Wichern, D.W., Churchill, G.A., 1978. A comparison of ridge estimators. Technometrics 30, 221-227.