What is the Delaunay triangulation in ? (original) (raw)

Next: Computing the Delaunay complex Up: Voronoi Diagram and Delaunay Previous: What is Voronoi diagram Contents

See also 3.2, 3.1.

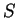Let $ S$ be a set of 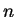$ n$ points in 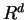$ R^d$ . The convex hull 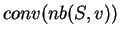$ conv(nb(S, v))$ of the nearest neighbor set of a Voronoi vertex 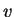$ v$ is called the Delaunay cell of 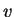$ v$ . The Delaunay complex (or triangulation) of 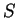$ S$ is a partition of the convex hull 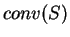$ conv(S)$ into the Delaunay cells of Voronoi vertices together with their faces.

$\includegraphics[height=40mm]{vtest_draw_vode}$

The Delaunay complex is not in general a triangulation but becomes a triangulation when the input points are in_general position_ (or nondegenerate), i.e. no 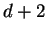$ d+2$ points are cospherical or equivalently there is no point 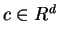$c\in R^d$ whose nearest neighbor set has more than 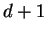$ d+1$ elements.

The Delaunay complex is dual to the Voronoi diagram 3.2in the sense that there is a natural bijection between the two complexes which reverses the face inclusions.

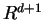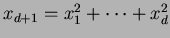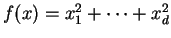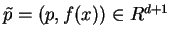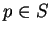There is a direct way to represent the Delaunay complex, just like the Voronoi diagram 3.2. In fact, it uses the same paraboloid in $R^{d+1}$ : $x_{d+1} = x_1^2 + \cdots + x_d^2$ . Let $f(x) = x_1^2 + \cdots + x_d^2$ , and let $\tilde{p}= (p, f(x)) \in R^{d+1}$ for $p \in S$ . Then the so-called lower hull of the lifted points 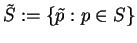$\tilde{S}:=\{\tilde{p}: p\in S\}$ represents the Delaunay complex. More precisely, let

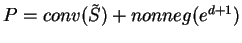
$\displaystyle P = conv(\tilde{S}) + nonneg(e^{d+1})$

where 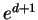$e^{d+1}$ is the unit vector in 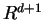$R^{d+1}$ whose last component is 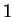$ 1$ . Thus 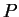$ P$ is the unbounded convex polyhedron consisting of 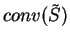$conv(\tilde{S})$ and any nonnegative shifts by the ``upper'' direction 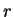$ r$ . The nontrivial claim is that the the boundary complex of 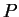$ P$ projects to the Delaunay complex: any facet of 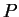$ P$ which is not parallel to the vertical direction 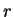$ r$ is a Delaunay cell once its last coordinate is ignored, and any Delaunay cell is represented this way.

Next: Computing the Delaunay complex Up: Voronoi Diagram and Delaunay Previous: What is Voronoi diagram Contents

Komei Fukuda 2004-08-26