Urban Heat Island Effects Have Not Yet Been Removed from Official GHCN Warming Trends « Roy Spencer, PhD (original) (raw)

October 25th, 2024 by Roy W. Spencer, Ph. D.

UPDATE (28 Oct. 2024): In response to concerns regarding the large amount of scatter in the data plots presented below, and the claims I make based upon those regressions, I have replaced all plots which now contain additional regression statistics. These statistics demonstrate high confidence. What many people don’t realize is that diagnosed regression slopes (and regression intercepts) can have high confidence despite low correlations (large scatter) if there are many data points. I will be posting a new article today showing an example of this.

Our paper (co-authored by John Christy and Danny Braswell) on computing the urban heat island (UHI) effect as a function of population density (PD) is now in the final stages of review after a 3rd round of edits, and I’m hopeful it will be accepted for publication soon. So far, I’ve only used Tavg data (the average of daily maximum and minimum temperatures) in developing and testing the method, and the paper uses only contiguous U.S. summertime data (June, July, August), which is what I will address here.

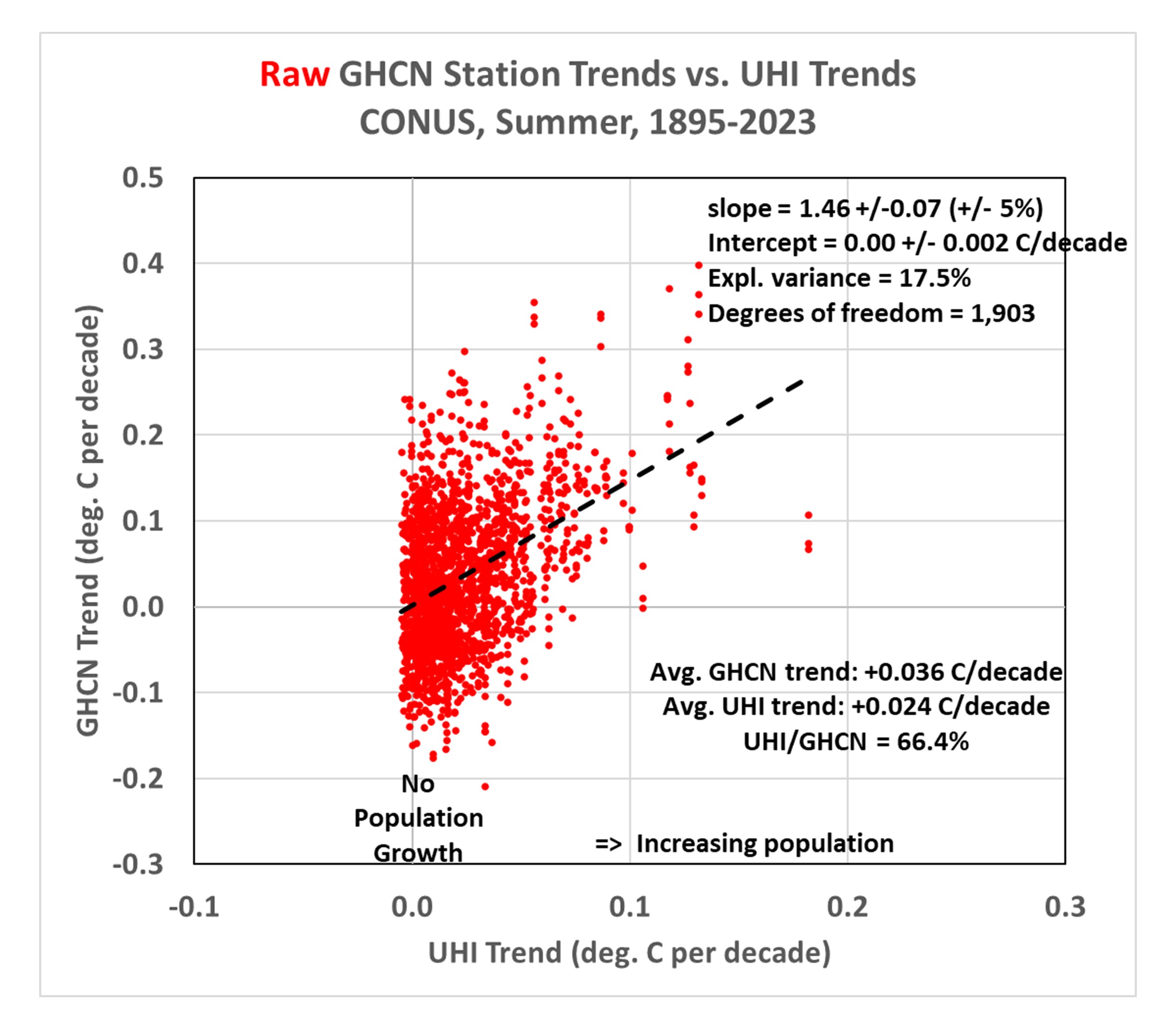
The method allows us to compute UHI trends using global gridded PD datasets that extend back to the 1800s. These UHI trends can then be compared to GHCN station temperature trends. If I do this for all U.S. GHCN stations having at least 120 years of complete monthly (June, July, or August) data out of 129 potential years during 1895-2023, the following plot shows some interesting results. (I begin with the “raw” data so we can then examine how homogenization changes the results.) Note the following plots have been updated to include regression statistics which demonstrate, despite low explained variances, the resulting regression slopes and intercepts have high confidence, due to the large number of data points (GHCN stations) contained in the plots.

1. The greater a station’s population growth, the greater the observed warming trend. This is pretty convincing evidence that the raw GHCN data has substantial UHI effects impacting the computed trends (probably no surprise here). Note the UHI temperature trend averages 66% of the raw temperature trends.
2. The regression line fit to the data intercepting zero shows that those stations with no population growth have, on average, no warming trend. While this might lead some to conclude there has been no net warming in the U.S. during 1895-2023, it must be remembered these are raw data, with no adjustments for time-of-observation (TOBS) changes or instrumentation type changes which might have biased most or all of the stations toward lower temperature trends.

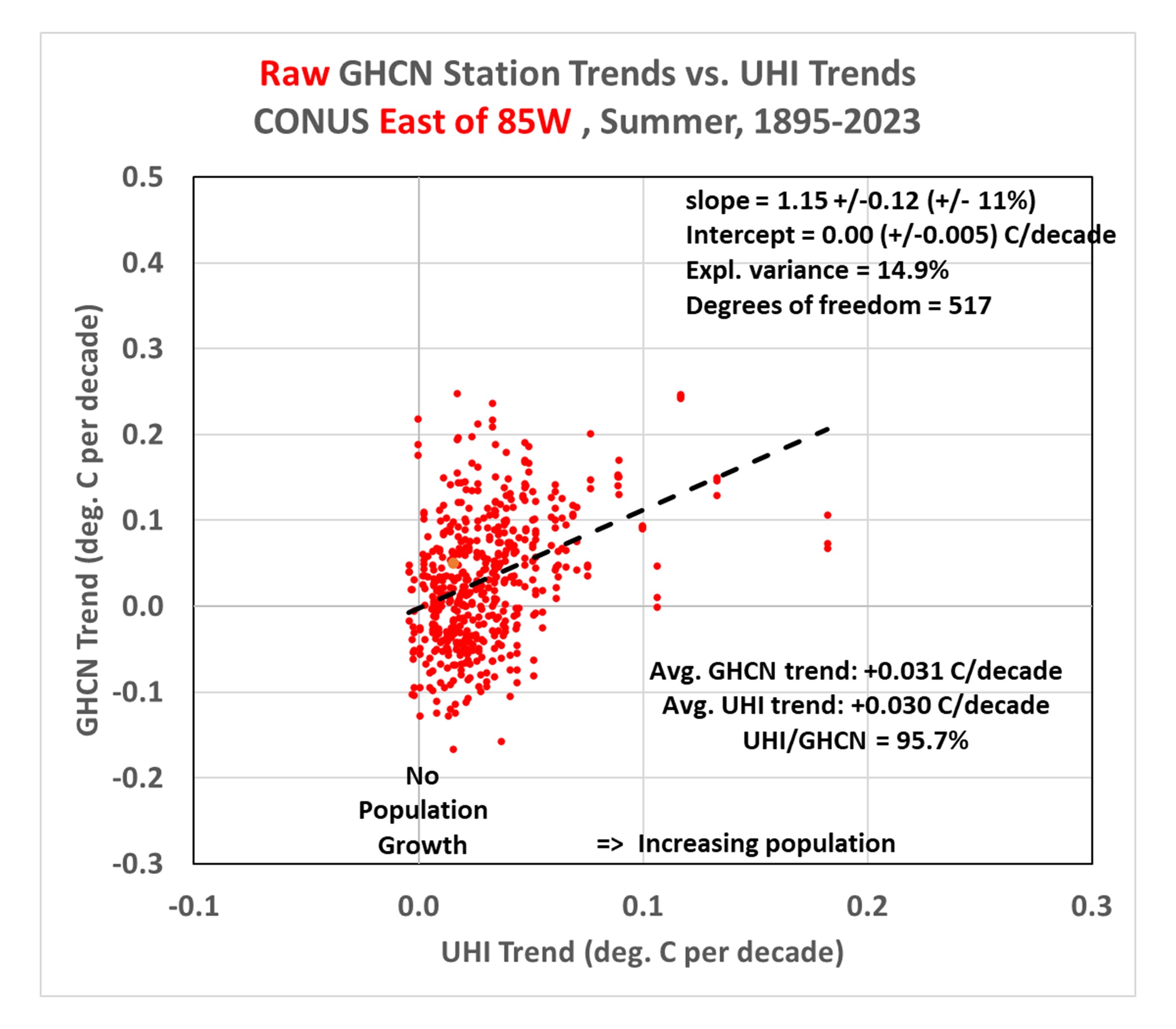
Since most of the rural stations (many of which have experienced little population growth) are in the western U.S., and there can be differences in actual temperature trends between the eastern and western U.S., let’s look at how things change if we just examine just the eastern U.S. (Ohio to the Florida peninsula, eastward):

This shows the Eastern U.S. has features similar to the U.S. as a whole, with a regression line intercept of zero (again) indicating those stations with no population growth have (on average) no warming trend in the raw GHCN data. But now, amazingly, the average UHI trend is over 95% of the raw station trends (!) This would seemingly suggest essentially all of the reported warming during 1895-2023 over the eastern U.S. has been due to the urbanization effect… if there are no systematic biases in the raw Tavg data that would cause those trends to be biased low. Also, as will be discussed below, this is the the period 1895-2023… the results for more recent decades are somewhat different.

Homogenization of the GHCN Data Produces Some Strange Effects

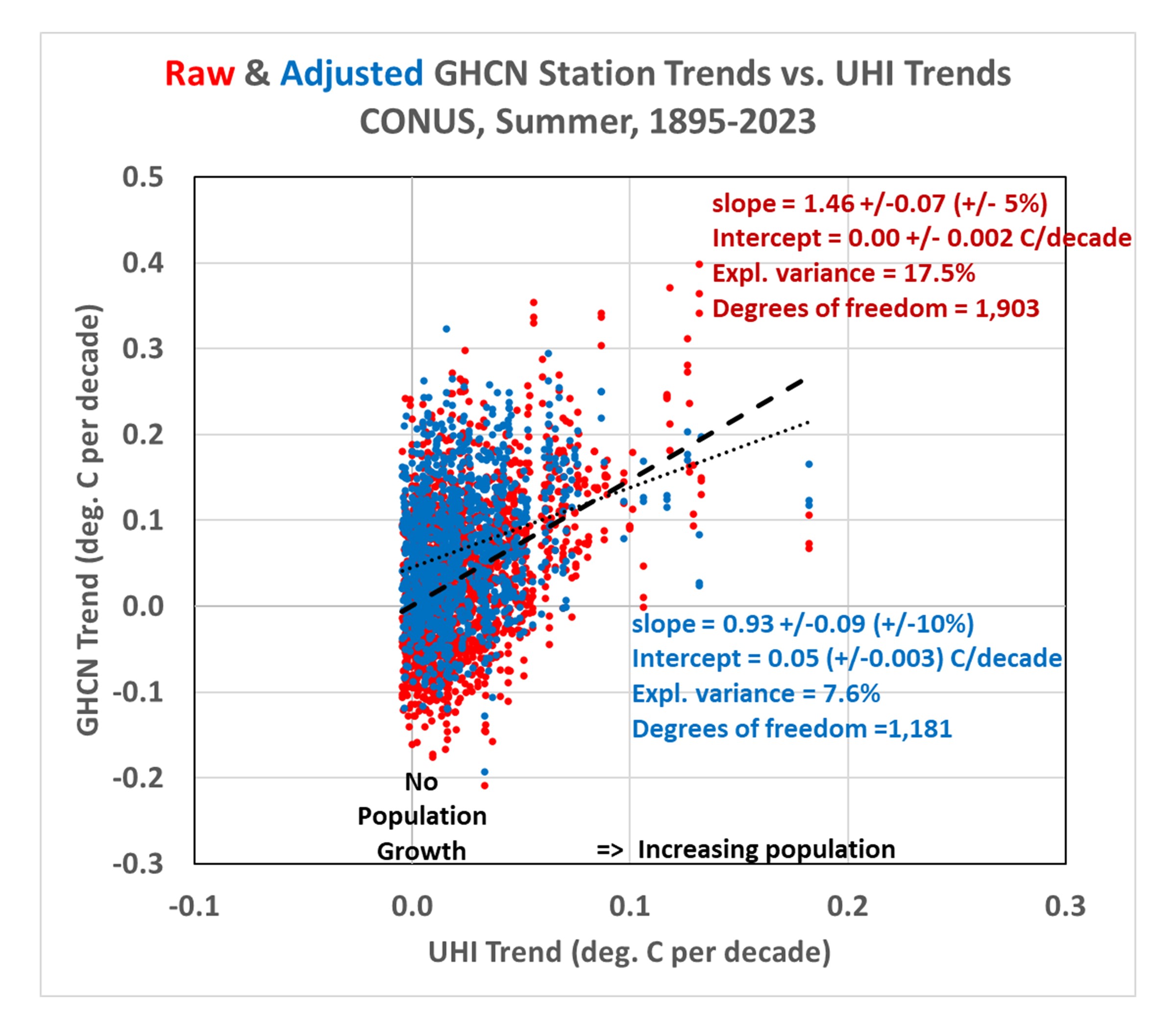
Next, let’s look at how the adjusted (homogenized) GHCN temperature trends compare to the UHI warming trends. Recall that the Pairwise Homogenization Algorithm (PHA) used by NOAA to create the “adjusted” GHCN dataset (which is the basis for official temperature statistics coming from the government) identifies and adjusts for step-changes in time at individual stations by comparing their temperature time series to the time series from surrounding stations. If we plot the adjusted data trend along with the raw data trends, the following figure shows some curious changes.

Here’s what homogenizations has done to the raw temperature data:

1. Stations with no population growth (that had on average no warming trend) now have a warming trend. I can’t explain this. It might be the “urban blending” artifact of the PHA algorithm discussed by Katata et al. (2023, and references therein) whereby homogenization doesn’t adjust urban stations to “look like” rural stations, but instead tends to smooth out the differences between neighboring stations, causing a “bleeding” of urban effects into the rural stations.
2. Stations with large population growth have had their warming trends reduced. This is the intended effect of homogenization.
3. There still exists a UHI effect in the homogenized trends, but it has been reduced by about 50% compared to the raw trends. This suggests the PHA algorithm is only partially removing spurious warming signals from increasing urbanization.
4. **Homogenization has caused the all-station average warming trend to nearly double (+89%), from +0.036 to +0.067 deg. C per decade.**I cannot explain this. It might be due to real effects from changes in instrumentation, the time-of-observation (TOBS) adjustment, an unintended artifact of the PHA algorithm, or some combination of all three.

Does This Mean Recent Warming In The U.S. Is Negligible?

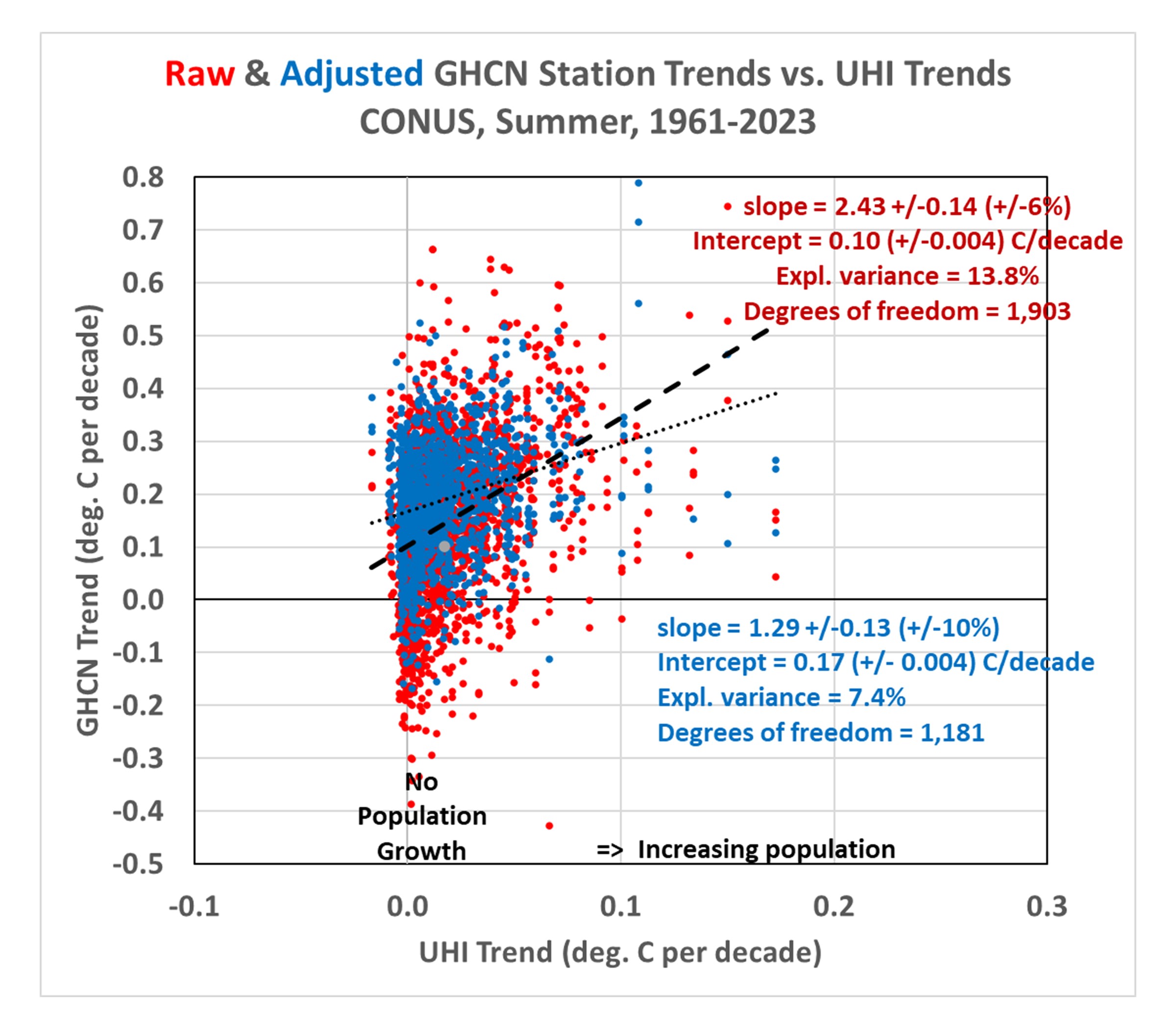
Maybe not. While it does suggest problems with warming trends since 1895, if we examine the most recent period of warming (say, since 1961…a date I chose arbitrarily), we find considerably stronger warming trends.

Note that the GHCN trends since 1961 are nearly the same from raw (+0.192 C/decade) as from homogenized (+0.193 C/decade) data. The average UHI warming trend is only about 13% of the raw GHCN trend, and 10% of the homogenized trend, indicating little of the GHCN warming trend can be attributed to increases in population density.

But there still remains an urbanization signal in both the raw and adjusted data, as indicated by the non-zero regression slopes. One possible interpretation of these results is that, if the homogenization algorithm is distorting the station trends, and if we can use the raw GHCN data as a more accurate representation of reality, then the regression intercept of +0.10 deg. C/decade becomes the best estimate of the all-station average warming trend if NONE of the stations had any growth in population. That is little more than 50% of the homogenized data warming trend of +0.192 deg. C/decade.

What Does It All Mean?

First, there is evidence supporting the “urban blending” hypothesis of Katata et al., whereby the homogenization algorithm inadvertently blends urban station characteristics into rural temperature data. This appears to increase the all-station average temperature trend.

Second, homogenization appears to only remove about 50% of the UHI signal. Even after homogenization, GHCN temperature trends tend to be higher for stations with large population growth, lower for stations with little population growth. There is some evidence that truly rural stations would have only about 50% of the warming averaged across all U.S. stations, which is consistent with Anthony Watts’ estimates based upon restricting analysis to only those best-sited stations.

These results suggest there is now additional reason to distrust the official temperature trends reported for U.S. weather stations. They are, on average, too warm. By how much? That remains to be determined. Our method provides the first way (that I know of) to independently estimate the urban warming effect over time, albeit in an average sense (that is, it is accurate for the average across many stations, but its accuracy at individual stations is unknown). As my career winds down, I hope others in the future will extend this type of analysis.

[To see what the total UHI signal is in various calendar months around the world as of 2023, here are the hi-res images: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec. More details of our method, along with links to monthly ArcGIS-format files of global UHI grids since 1800 (Version 0) are contained in my blog post from November, 2023.]