Activation functions in Neural Networks (original) (raw)

While building a neural network, one key decision is selecting the Activation Function for both the hidden layer and the output layer. It is a mathematical function applied to the output of a neuron. It introduces non-linearity into the model, allowing the network to learn and represent complex patterns in the data. Without this non-linearity feature a neural network would behave like a linear regression model no matter how many layers it has.

Activation function decides whether a neuron should be activated by calculating the weighted sum of inputs and adding a bias term. This helps the model make complex decisions and predictions by introducing non-linearities to the output of each neuron.

_Before diving into the activation function, you should have prior knowledge of the following topics:**Neural Networks****,** **Backpropagation

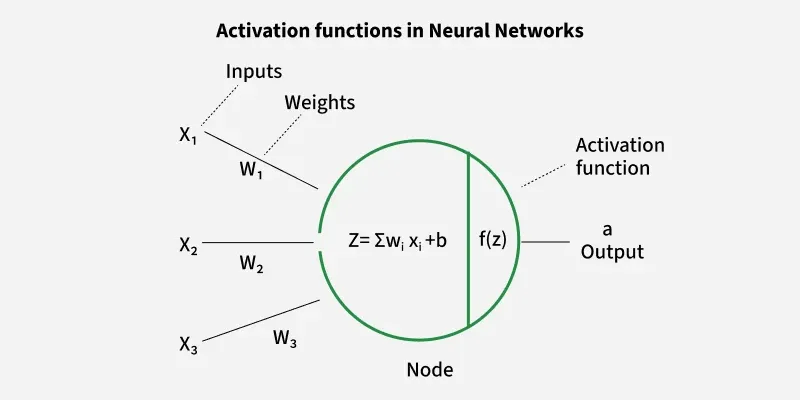
Activation Functions in neural Networks

Introducing Non-Linearity in Neural Network

Non-linearity means that the relationship between input and output is not a straight line. In simple terms the output does not change proportionally with the input. A common choice is the ReLU function defined as \sigma(x) = \max(0, x).

Imagine you want to classify apples and bananas based on their shape and color.

• If we use a linear function it can only separate them using a straight line.
• But real-world data is often more complex like overlapping colors, different lighting, etc.
• By adding a non-linear activation function like ReLU, Sigmoid or Tanh the network can create curved decision boundaries to separate them correctly.

Effect of Non-Linearity

The inclusion of the ReLU activation function \sigma allows h_1​ to introduce a non-linear decision boundary in the input space. This non-linearity enables the network to learn more complex patterns that are not possible with a purely linear model such as:

• Modeling functions that are not linearly separable.
• Increasing the capacity of the network to form multiple decision boundaries based on the combination of weights and biases.

Why is Non-Linearity Important in Neural Networks?

Neural networks consist of neurons that operate using weights, biases and activation functions.

In the learning process these weights and biases are updated based on the error produced at the output—a process known as backpropagation. Activation functions enable backpropagation by providing gradients that are essential for updating the weights and biases.

Without non-linearity even deep networks would be limited to solving only simple, linearly separable problems. Activation functions help neural networks to model highly complex data distributions and solve advanced deep learning tasks. Adding non-linear activation functions introduce flexibility and enable the network to learn more complex and abstract patterns from data.

Mathematical Proof of Need of Non-Linearity in Neural Networks

To illustrate the need for non-linearity in neural networks with a specific example let's consider a network with two input nodes (i_1 \text{and } i_2​), a single hidden layer containing neurons h_1 \text{ and } h_2 and an output neuron (out).

We will use w_1, w_2 as weights connecting the inputs to the hidden neuron and w_5​ as the weight connecting the hidden neuron to the output. We'll also include biases (b_1​ for the hidden neuron and b_2 for the output neuron) to complete the model.

1. **Input Layer: Two inputs i_1 and i_2​.
2. **Hidden Layer: Two neuron h_1​ and h_2
3. **Output Layer: One output neuron.

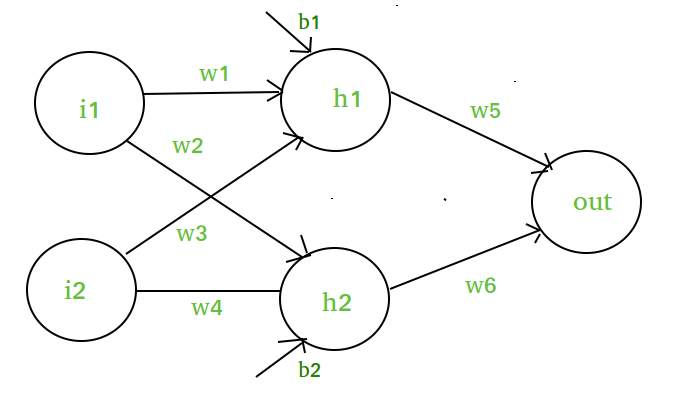
The input to the hidden neuron h_1 is calculated as a weighted sum of the inputs plus a bias:

{h_1} = i_1.w_1 + i_2.w_3 + b_1

{h_2} = i_1.w_2 + i_2.w_4 + b_2

The output neuron is then a weighted sum of the hidden neuron's output plus a bias:

\text{output} = h_1.w_5 + h_2.w_6 + \text{bias}

Here, h_1 , h_2 \text{ and output} are linear expressions.

In order to add non-linearity, we will be using sigmoid activation function in the output layer:

\sigma(x) = \frac{1}{1+e^{-x}}

\text{final output} = \sigma(h_1.w_5 + h_2.w_6 + \text{bias})

\text{final output} = \frac{1}{1+e^{-(h_1.w_5+h_2.w_6 + \text{bias})}}

This gives the final output of the network after applying the sigmoid activation function in output layers, introducing the desired non-linearity.

Types of Activation Functions in Deep Learning

**1. Linear Activation Function

Linear Activation Function resembles straight line define by y=x. No matter how many layers the neural network contains if they all use linear activation functions the output is a linear combination of the input.

• The range of the output spans from (-\infty \text{ to } + \infty).
• Linear activation function is used at just one place i.e. output layer.
• Using linear activation across all layers makes the network's ability to learn complex patterns limited.

Linear activation functions are useful for specific tasks but must be combined with non-linear functions to enhance the neural network’s learning and predictive capabilities.

Linear Activation Function or Identity Function returns the input as the output

2. Non-Linear Activation Functions

**1. Sigmoid Function

**Sigmoid Activation Function is characterized by 'S' shape. It is mathematically defined as A = \frac{1}{1 + e^{-x}}​. This formula ensures a smooth and continuous output that is essential for gradient-based optimization methods.

• It allows neural networks to handle and model complex patterns that linear equations cannot.
• The output ranges between 0 and 1, hence useful for binary classification.
• The function exhibits a steep gradient when x values are between -2 and 2. This sensitivity means that small changes in input x can cause significant changes in output y which is critical during the training process.

Sigmoid or Logistic Activation Function Graph

**2. Tanh Activation Function

**Tanh function(hyperbolic tangent function) is a shifted version of the sigmoid, allowing it to stretch across the y-axis. It is defined as:

f(x) = \tanh(x) = \frac{2}{1 + e^{-2x}} - 1.

Alternatively, it can be expressed using the sigmoid function:

\tanh(x) = 2 \times \text{sigmoid}(2x) - 1

• **Value Range: Outputs values from -1 to +1.
• **Non-linear: Enables modeling of complex data patterns.
• **Use in Hidden Layers: Commonly used in hidden layers due to its zero-centered output, facilitating easier learning for subsequent layers.

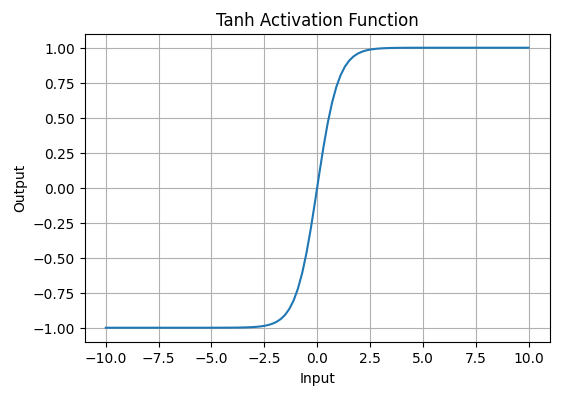
Tanh Activation Function

**3. ReLU (Rectified Linear Unit) **Function

**ReLU activation is defined by A(x) = \max(0,x), this means that if the input x is positive, ReLU returns x, if the input is negative, it returns 0.

• **Value Range: [0, \infty), meaning the function only outputs non-negative values.
• **Nature: It is a non-linear activation function, allowing neural networks to learn complex patterns and making backpropagation more efficient.
• **Advantage over other Activation: ReLU is less computationally expensive than tanh and sigmoid because it involves simpler mathematical operations. At a time only a few neurons are activated making the network sparse making it efficient and easy for computation.

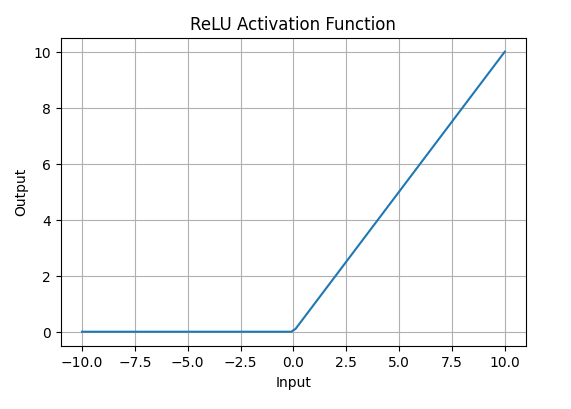
ReLU Activation Function

3. **Exponential Linear Units

**1. Softmax Function

**Softmax function is designed to handle multi-class classification problems. It transforms raw output scores from a neural network into probabilities. It works by squashing the output values of each class into the range of 0 to 1 while ensuring that the sum of all probabilities equals 1.

• Softmax is a non-linear activation function.
• The Softmax function ensures that each class is assigned a probability, helping to identify which class the input belongs to.

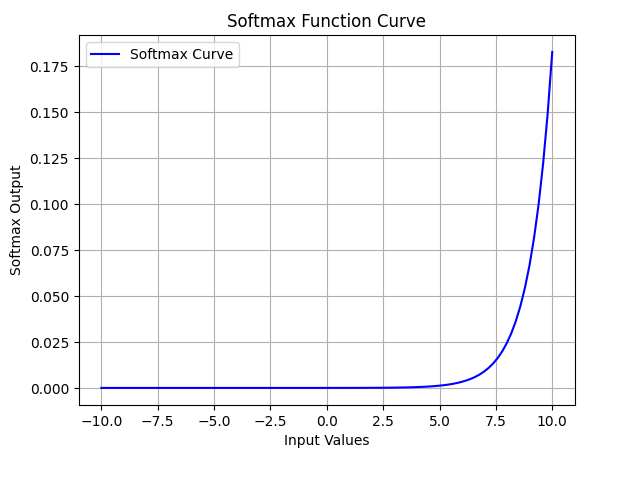
Softmax Activation Function

**2. SoftPlus Function

**Softplus function is defined mathematically as: A(x) = \log(1 + e^x).

This equation ensures that the output is always positive and differentiable at all points which is an advantage over the traditional ReLU function.

• **Nature: The Softplus function is non-linear.
• **Range: The function outputs values in the range (0, \infty), similar to ReLU, but without the hard zero threshold that ReLU has.
• **Smoothness: Softplus is a smooth, continuous function, meaning it avoids the sharp discontinuities of ReLU which can sometimes lead to problems during optimization.

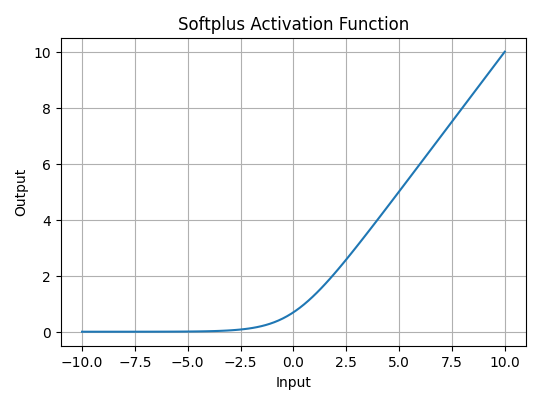
Softplus Activation Function

Impact of Activation Functions on Model Performance

The choice of activation function has a direct impact on the performance of a neural network in several ways:

1. **Convergence Speed: Functions like ReLU allow faster training by avoiding the vanishing gradient problem while Sigmoid and Tanh can slow down convergence in deep networks.
2. **Gradient Flow: Activation functions like ReLU ensure better gradient flow, helping deeper layers learn effectively. In contrast Sigmoid can lead to small gradients, hindering learning in deep layers.
3. **Model Complexity: Activation functions like Softmax allow the model to handle complex multi-class problems, whereas simpler functions like ReLU or Leaky ReLU are used for basic layers.

Activation functions are the backbone of neural networks enabling them to capture non-linear relationships in data. From classic functions like Sigmoid and Tanh to modern variants like ReLU and Swish, each has its place in different types of neural networks. The key is to understand their behavior and choose the right one based on your model’s needs.