Adjacency Matrix Representation (original) (raw)

Last Updated : 19 Mar, 2025

**Adjacency Matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. An adjacency matrix is a simple and straightforward way to represent graphs and is particularly useful for dense graphs.

Table of Content

What is Adjacency Matrix?

Adjacency Matrix is a square matrix used to represent a finite graph by storing the relationships between the nodes in their respective cells. For a graph with **V vertices, the adjacency matrix A is an V X V matrix or 2D array.

1. Adjacency Matrix for Undirected and Unweighted graph:

Consider an Undirected and Unweighted graph **G with **4 vertices and **3 edges. For the graph G, the adjacency matrix would look like:

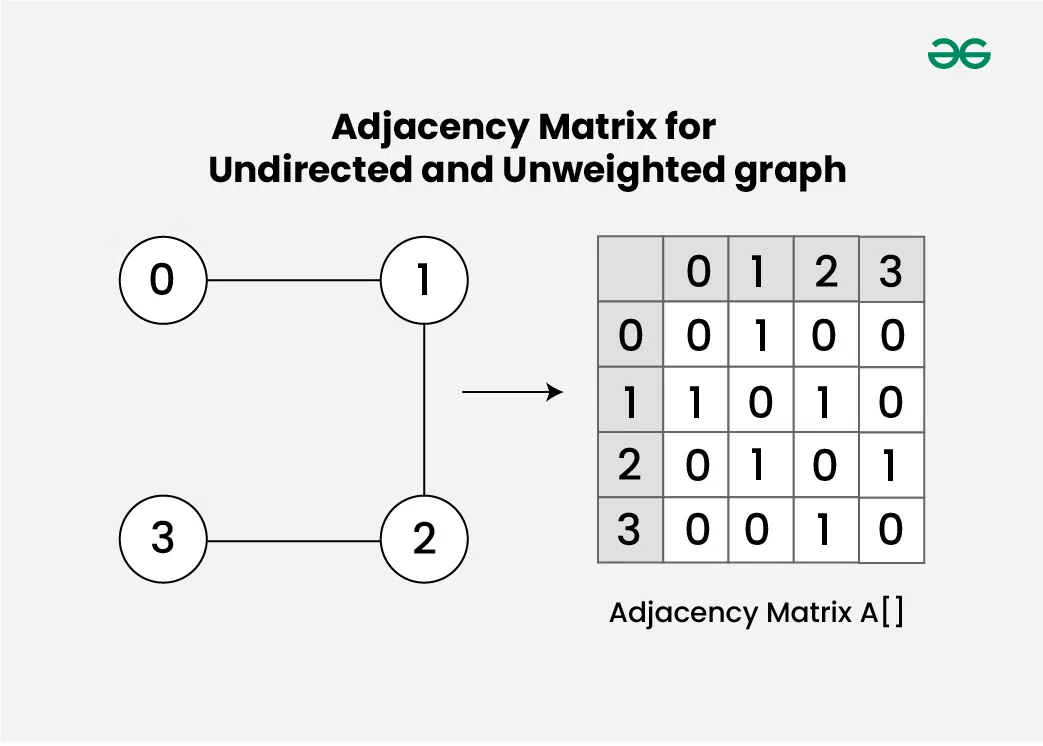
Adjacency-Matrix-for-Undirected-and-Unweighted-graph

Here's how to interpret the matrix:

Below is a program to create an adjacency matrix for an unweighted and undirected graph:

C++ `

// C++ program to demonstrate Adjacency Matrix // representation of undirected and unweighted graph #include <bits/stdc++.h> using namespace std;

void addEdge(vector<vector> &mat, int i, int j) { mat[i][j] = 1; mat[j][i] = 1; // Since the graph is undirected }

void displayMatrix(vector<vector> &mat) { int V = mat.size(); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) cout << mat[i][j] << " "; cout << endl; } }

int main() {

// Create a graph with 4 vertices and no edges
// Note that all values are initialized as 0
int V = 4;
vector<vector<int>> mat(V, vector<int>(V, 0));

// Now add edges one by one
addEdge(mat, 0, 1);
addEdge(mat, 0, 2);
addEdge(mat, 1, 2);
addEdge(mat, 2, 3);

/* Alternatively we can also create using below
   code if we know all edges in advacem

 vector<vector<int>> mat = {{ 0, 1, 0, 0 },
                           { 1, 0, 1, 0 },
                           { 0, 1, 0, 1 },
                           { 0, 0, 1, 0 } }; */

cout << "Adjacency Matrix Representation" << endl;
displayMatrix(mat);

return 0;

}

C

#include<stdio.h>

#define V 4

void addEdge(int mat[V][V], int i, int j) { mat[i][j] = 1; mat[j][i] = 1; // Since the graph is undirected }

void displayMatrix(int mat[V][V]) { for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) printf("%d ", mat[i][j]); printf("\n"); } }

int main() { // Create a graph with 4 vertices and no edges // Note that all values are initialized as 0 int mat[V][V] = {0};

// Now add edges one by one
addEdge(mat, 0, 1);
addEdge(mat, 0, 2);
addEdge(mat, 1, 2);
addEdge(mat, 2, 3);

/* Alternatively, we can also create using the below
   code if we know all edges in advance

int mat[V][V] = {
    {0, 1, 0, 0},
    {1, 0, 1, 0},
    {0, 1, 0, 1},
    {0, 0, 1, 0}
}; */

printf("Adjacency Matrix Representation\n");
displayMatrix(mat);

return 0;

}

Java

import java.util.Arrays;

public class GfG {

public static void addEdge(int[][] mat, int i, int j) {
    mat[i][j] = 1;
    mat[j][i] = 1; // Since the graph is undirected
}

public static void displayMatrix(int[][] mat) {
    for (int[] row : mat) {
        for (int val : row) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}

public static void main(String[] args) {

    // Create a graph with 4 vertices and no edges
    // Note that all values are initialized as 0
    int V = 4;
    int[][] mat = new int[V][V];

    // Now add edges one by one
    addEdge(mat, 0, 1);
    addEdge(mat, 0, 2);
    addEdge(mat, 1, 2);
    addEdge(mat, 2, 3);

    /* Alternatively we can also create using below
       code if we know all edges in advance

     int[][] mat = {{ 0, 1, 0, 0 },
                    { 1, 0, 1, 0 },
                    { 0, 1, 0, 1 },
                    { 0, 0, 1, 0 } }; */

    System.out.println("Adjacency Matrix Representation");
    displayMatrix(mat);
}

}

Python

def add_edge(mat, i, j):

# Add an edge between two vertices
mat[i][j] = 1  # Graph is 
mat[j][i] = 1  # Undirected

def display_matrix(mat):

# Display the adjacency matrix
for row in mat:
    print(" ".join(map(str, row)))

Main function to run the program

if name == "main": V = 4 # Number of vertices mat = [[0] * V for _ in range(V)] 

# Add edges to the graph
add_edge(mat, 0, 1)
add_edge(mat, 0, 2)
add_edge(mat, 1, 2)
add_edge(mat, 2, 3)

# Optionally, initialize matrix directly
"""
mat = [
    [0, 1, 0, 0],
    [1, 0, 1, 0],
    [0, 1, 0, 1],
    [0, 0, 1, 0]
]
"""

# Display adjacency matrix
print("Adjacency Matrix:")
display_matrix(mat)

C#

using System;

public class GfG { // Add an edge between two vertices public static void AddEdge(int[,] mat, int i, int j) { mat[i, j] = 1; // Since the graph is mat[j, i] = 1; // undirected }

// Display the adjacency matrix
public static void DisplayMatrix(int[,] mat)
{
    int V = mat.GetLength(0); 
    for (int i = 0; i < V; i++)
    {
        for (int j = 0; j < V; j++)
        {
            Console.Write(mat[i, j] + " ");
        }
        Console.WriteLine(); 
    }
}

// Main method to run the program
public static void Main(string[] args)
{
    int V = 4; // Number of vertices
    int[,] mat = new int[V, V]; // Initialize matrix

    // Add edges to the graph
    AddEdge(mat, 0, 1);
    AddEdge(mat, 0, 2);
    AddEdge(mat, 1, 2);
    AddEdge(mat, 2, 3);

    // Optionally, initialize matrix directly
    /*
    int[,] mat = new int[,]
    {
        { 0, 1, 0, 0 },
        { 1, 0, 1, 0 },
        { 0, 1, 0, 1 },
        { 0, 0, 1, 0 }
    };
    */

    // Display adjacency matrix
    Console.WriteLine("Adjacency Matrix:");
    DisplayMatrix(mat);
}

}

JavaScript

function addEdge(mat, i, j) { mat[i][j] = 1; // Graph is mat[j][i] = 1; // undirected }

function displayMatrix(mat) { // Display the adjacency matrix for (const row of mat) { console.log(row.join(" ")); } }

// Main function to run the program const V = 4; // Number of vertices

// Initialize matrix let mat = Array.from({ length: V }, () => Array(V).fill(0));

// Add edges to the graph addEdge(mat, 0, 1); addEdge(mat, 0, 2); addEdge(mat, 1, 2); addEdge(mat, 2, 3);

/* Optionally, initialize matrix directly let mat = [ [0, 1, 0, 0], [1, 0, 1, 0], [0, 1, 0, 1], [0, 0, 1, 0] ]; */

// Display adjacency matrix console.log("Adjacency Matrix:"); displayMatrix(mat);

`

Output

Adjacency Matrix Representation 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 0

2. Adjacency Matrix for Undirected and Weighted graph:

Consider an Undirected and Weighted graph **G with **5 vertices and **5 edges. For the graph G, the adjacency matrix would look like:

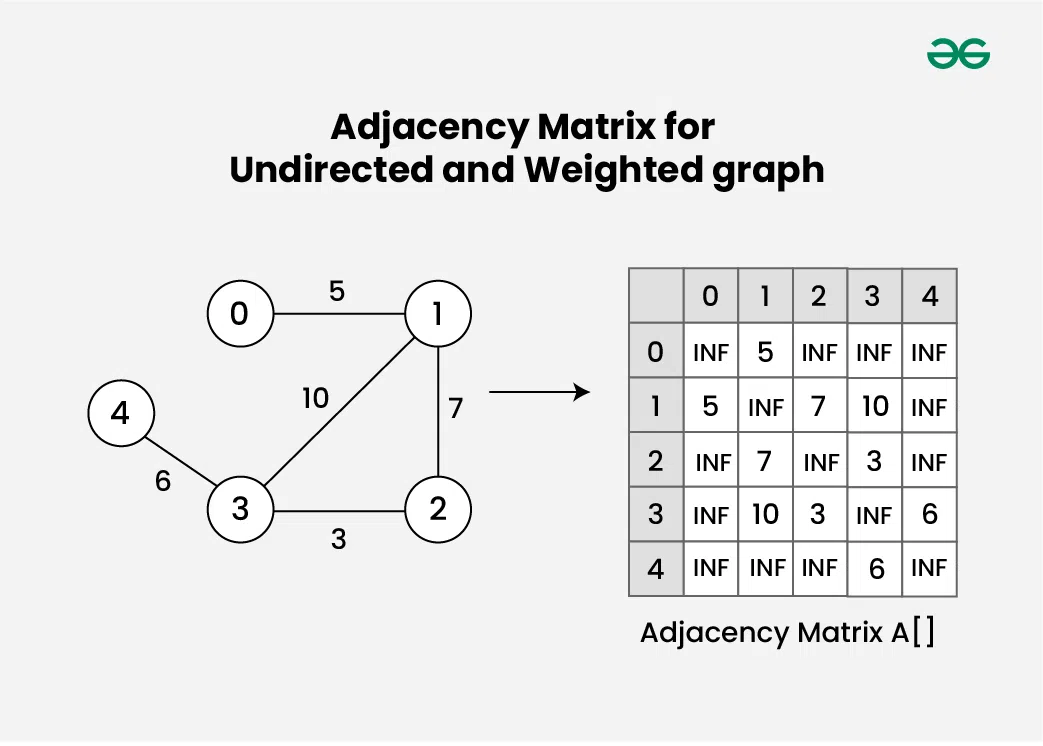
Adjacency-Matrix-for-Undirected-and-Weighted-graph

Here's how to interpret the matrix:

3. Adjacency Matrix for Directed and Unweighted graph:

Consider an Directed and Unweighted graph **G with 4 vertices and 4 edges. For the graph G, the adjacency matrix would look like:

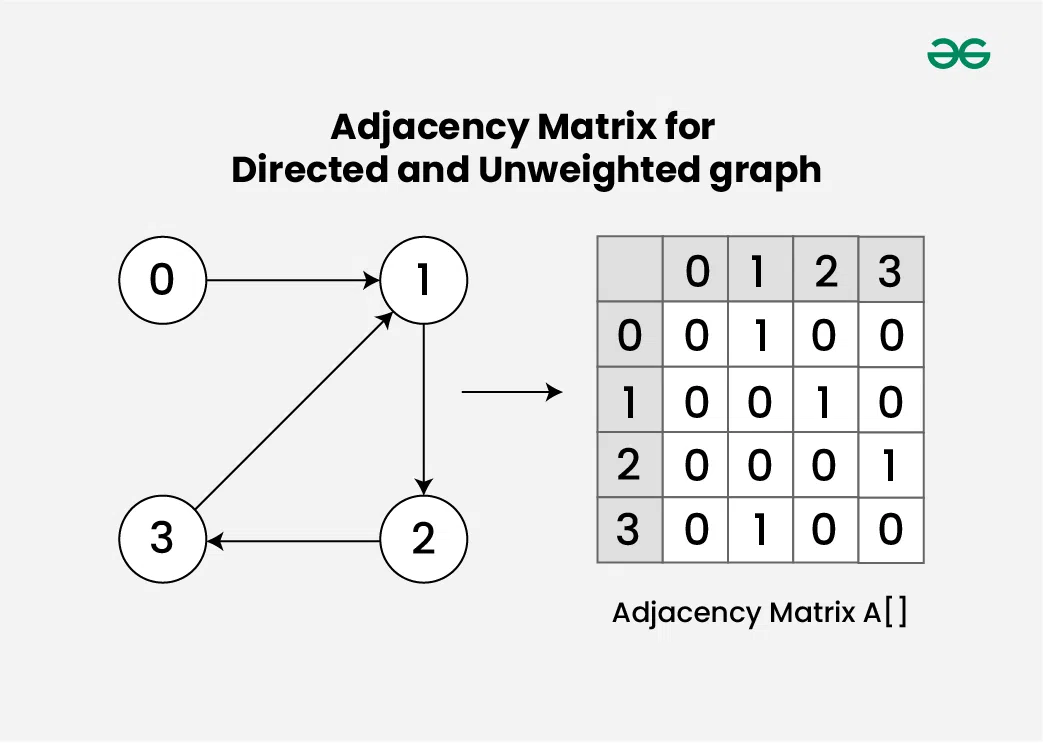
Adjacency-Matrix-for-Directed-and-Unweighted-graph

Here's how to interpret the matrix:

4. Adjacency Matrix for Directed and Weighted graph:

Consider an Directed and Weighted graph **G with 5 vertices and 6 edges. For the graph G, the adjacency matrix would look like:

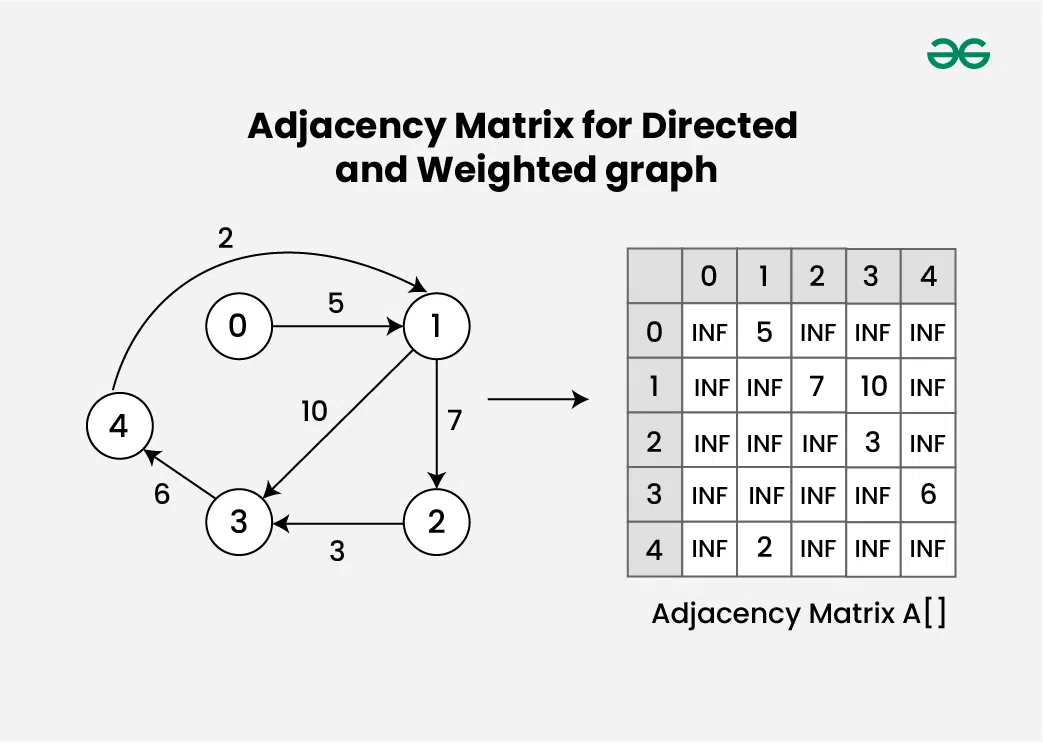
Adjacency-Matrix-for-Directed-and-Weighted-graph

Here's how to interpret the matrix:

Properties of Adjacency Matrix

Applications of Adjacency Matrix:

Advantages of Adjacency Matrix:

Disadvantages of Adjacency Matrix: