Advanced Quick Sort (Hybrid Algorithm) (original) (raw)
Last Updated : 12 Jan, 2023
Prerequisites: Insertion Sort, Quick Sort, Selection Sort
In this article, a Hybrid algorithm with the combination of quick sort and insertion sort is implemented. As the name suggests, the Hybrid algorithm combines more than one algorithm.
Why Hybrid algorithm:
Quicksort algorithm is efficient if the size of the input is very large. But, insertion sort is more efficient than quick sort in case of small arrays as the number of comparisons and swaps are less compared to quicksort. So we combine the two algorithms to sort efficiently using both approaches.
Note: Selectionsort algorithm can also be used to combine with quicksort. Though the time complexity is of O(N2), these algorithms prove to be efficient in this case because these are used only when the size of the array is less than a threshold value(10 in this article).
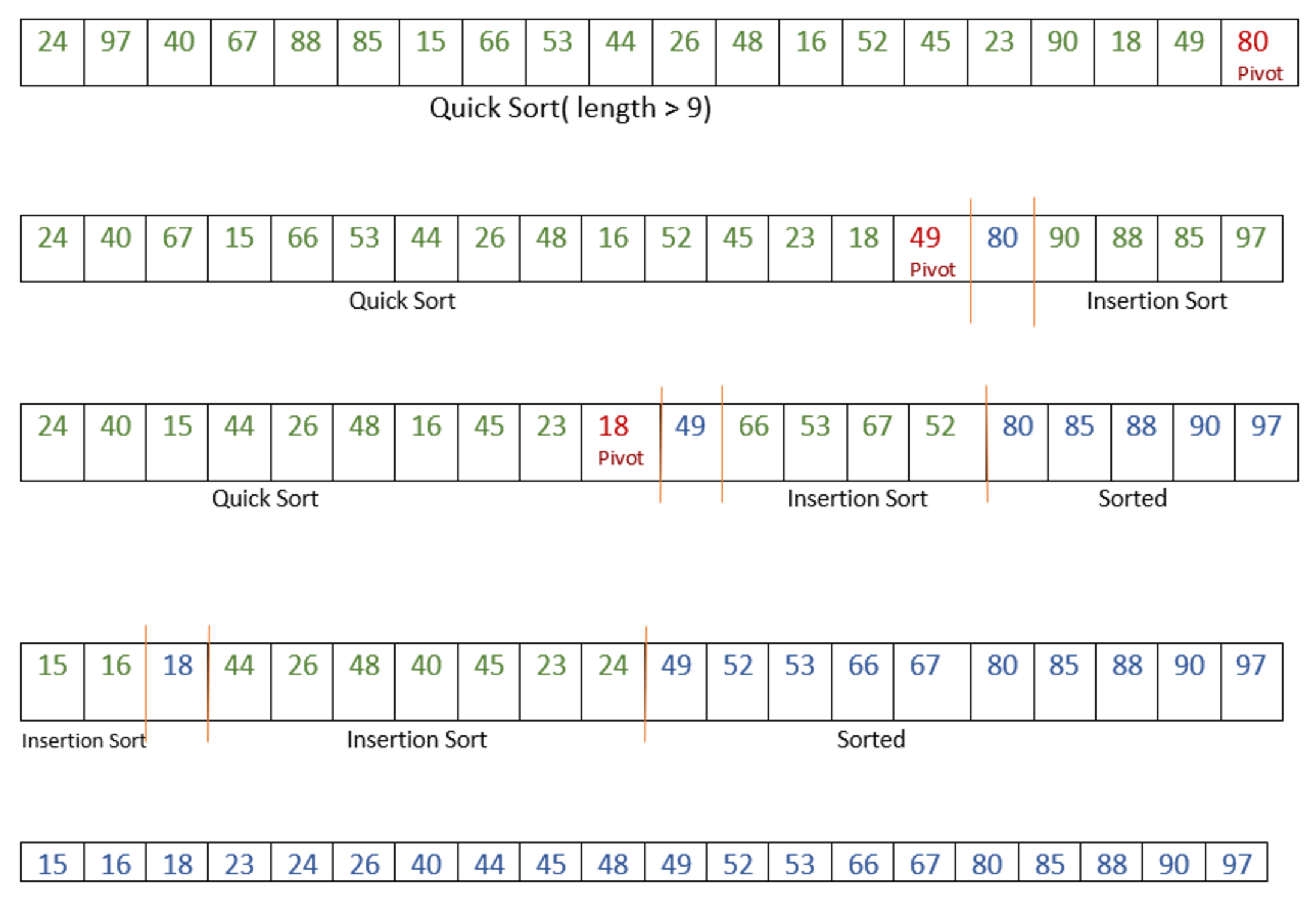
Dry run of the algorithm:
Let arr[] = {24, 97, 40, 67, 88, 85, 15, 66, 53, 44, 26, 48, 16, 52, 45, 23, 90, 18, 49, 80}
Example explanation
Approach: The idea is to use recursion and continuously find the size of the array. If the size is greater than the threshold value(10), then the quicksort function is called for that portion of the array. Else, insertion sort is called.
Below is the implementation of the Hybrid algorithm:
C++ `
// C++ implementation of the above approach
#include<bits/stdc++.h> using namespace std;
// Function to perform the insertion sort
void insertion_sort(int arr[], int low, int n) {
for(int i=low+1;i<n+1;i++)
{
int val = arr[i] ;
int j = i ;
while (j>low && arr[j-1]>val)
{
arr[j]= arr[j-1] ;
j-= 1;
}
arr[j]= val ;
} }
//The following two functions are used // to perform quicksort on the array.
// Partition function for quicksort
int partition(int arr[], int low, int high) { int pivot = arr[high] ; int i ,j; i = low; j = low;
for (int i = low; i < high; i++) { if(arr[i]<pivot) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; j += 1; } }
int temp = arr[j];
arr[j] = arr[high];
arr[high] = temp;return j; }
// Function to call the partition function // and perform quick sort on the array
void quick_sort(int arr[], int low,int high) { if (low < high) { int pivot = partition(arr, low, high); quick_sort(arr, low, pivot-1) ; quick_sort(arr, pivot + 1, high) ;
} }
// Hybrid function -> Quick + Insertion sort
void hybrid_quick_sort(int arr[], int low, int high) { while (low < high) {
// If the size of the array is less
// than threshold apply insertion sort
// and stop recursion
if (high-low + 1 < 10)
{
insertion_sort(arr, low, high);
break;
}
else
{
int pivot = partition(arr, low, high) ;
// Optimised quicksort which works on
// the smaller arrays first
// If the left side of the pivot
// is less than right, sort left part
// and move to the right part of the array
if (pivot-low<high-pivot)
{
hybrid_quick_sort(arr, low, pivot - 1);
low = pivot + 1;
}
else
{
// If the right side of pivot is less
// than left, sort right side and
// move to the left side
hybrid_quick_sort(arr, pivot + 1, high);
high = pivot-1;
}
}} } // Driver Code int main() { int arr[21] = { 24, 97, 40, 67, 88, 85, 15, 66, 53, 44, 26, 48, 16, 52, 45, 23, 90, 18, 49, 80, 23 };
hybrid_quick_sort(arr, 0, 20);
for(int i = 0; i < 21; i++) cout << arr[i] << ", "; }
// This code is contributed by ishayadav2918
Java
/*package whatever //do not write package name here / import java.io.; class GFG {
private static void insertionSort(int a[], int low,
int high)
{
for (int i = low + 1; i <= high; i++) {
for (int j = i - 1; j >= low; j--) {
if (a[j] > a[j + 1]) {
// Swap
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
else
break;
}
}
}
private static int partition(int arr[], int low,
int high)
{
int pivot = arr[high];
int i = low;
int j = low;
while (i <= high) {
if (arr[i] > pivot)
i++;
else {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j++;
}
}
return j - 1;
}
public static void hybridQuickSort(int arr[], int low,
int high)
{
while (low < high) {
// Check if array size on which we will be working is less than 10
if (high - low < 10) {
insertionSort(arr, low, high);
break;
}
else {
int pivot = partition(arr, low, high);
// We will do recursion on small size
// subarray So we can check pivot - low and
// pivot - high
if (pivot - low < pivot - high) {
hybridQuickSort(arr, low, pivot - 1);
low = pivot + 1;
}
else {
hybridQuickSort(arr, pivot + 1, high);
high = pivot - 1;
}
}
}
}// Driver code public static void main(String[] args) {
int arr[]
= { 24, 97, 40, 67, 88, 85, 15, 66, 53, 44, 26,
48, 16, 52, 45, 23, 90, 18, 49, 80, 23 };
hybridQuickSort(arr, 0, arr.length - 1);
for (int i : arr)
System.out.print(i + " ");
}}
// This code is contribute by @mahi_07
Python3
Python implementation of the above approach
Function to perform the insertion sort
def insertion_sort(arr, low, n): for i in range(low + 1, n + 1): val = arr[i] j = i while j>low and arr[j-1]>val: arr[j]= arr[j-1] j-= 1 arr[j]= val
The following two functions are used
to perform quicksort on the array.
Partition function for quicksort
def partition(arr, low, high): pivot = arr[high] i = j = low for i in range(low, high): if arr[i]<pivot: a[i], a[j]= a[j], a[i] j+= 1 a[j], a[high]= a[high], a[j] return j
Function to call the partition function
and perform quick sort on the array
def quick_sort(arr, low, high): if low<high: pivot = partition(arr, low, high) quick_sort(arr, low, pivot-1) quick_sort(arr, pivot + 1, high) return arr
Hybrid function -> Quick + Insertion sort
def hybrid_quick_sort(arr, low, high): while low<high:
# If the size of the array is less
# than threshold apply insertion sort
# and stop recursion
if high-low + 1<10:
insertion_sort(arr, low, high)
break
else:
pivot = partition(arr, low, high)
# Optimised quicksort which works on
# the smaller arrays first
# If the left side of the pivot
# is less than right, sort left part
# and move to the right part of the array
if pivot-low<high-pivot:
hybrid_quick_sort(arr, low, pivot-1)
low = pivot + 1
else:
# If the right side of pivot is less
# than left, sort right side and
# move to the left side
hybrid_quick_sort(arr, pivot + 1, high)
high = pivot-1Driver code
a = [ 24, 97, 40, 67, 88, 85, 15, 66, 53, 44, 26, 48, 16, 52, 45, 23, 90, 18, 49, 80, 23 ] hybrid_quick_sort(a, 0, 20) print(a)
C#
// C# implementation of QuickSort
using System;
class GFG {
// Function to perform the insertion sort static void insertion_sort(int[] arr, int low, int n){ for(int i = low+1; i < n+1; i++){ int val = arr[i]; int j = i; while (j > low && arr[j-1] > val){ arr[j]= arr[j-1] ; j-= 1; } arr[j]= val; } }
// The following two function are used to // perform the quick sort on the array
// Partition function for quicksort static int partition(int[] arr, int low, int high) {
// pivot
int pivot = arr[high];
int i;
int j;
i = low;
j = low;
for (i = low; i < high; i++)
{
if (arr[i] < pivot)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
j += 1;
}
}
int temp2 = arr[j];
arr[j] = arr[high];
arr[high] = temp2;
return j;}
// Function to call the partition function // amd perform quick sort on the array static void quickSort(int[] arr, int low, int high) { if (low < high) { int pivot = partition(arr, low, high); quickSort(arr, low, pivot - 1); quickSort(arr, pivot + 1, high); } }
// Hybrid function -> Quick + Insertion Sort static void hybrid_quick_sort(int[] arr, int low, int high){ while(low < high){
// If the size of the array is less
// than threshold apply insertion sort
// and stop recursion
if(high+low+1 < 10){
insertion_sort(arr, low, high);
break;
}
else{
int pivot = partition(arr, low, high);
// Optimized quickSort which works on
// the smaller arrays first
// If the left side of the pivot
// is less than right, sort left part
// and move to the right part of the array
if(pivot-low < high-pivot){
hybrid_quick_sort(arr, low, pivot-1);
low = pivot-1;
}
else{
// If the right side of pivot is less
// than left, sort right side and
// move to the left side
hybrid_quick_sort(arr, pivot+1, high);
high = pivot - 1;
}
}
}} // Function to print an array static void printArray(int[] arr, int size) { for (int i = 0; i < size; i++) Console.Write(arr[i] + ", ");
Console.WriteLine();}
// Driver Code public static void Main() { int[] arr = { 24, 97, 40, 67, 88, 85, 15, 66, 53, 44, 26, 48, 16, 52, 45, 23, 90, 18, 49, 80, 23 };
int n = arr.Length;
hybrid_quick_sort(arr, 0, n-1);
printArray(arr, n);} }
// This code is contributed by Aditya Sharma
JavaScript
JavaScript
`
Output
15, 16, 18, 23, 23, 24, 26, 40, 44, 45, 48, 49, 52, 53, 66, 67, 80, 85, 88, 90, 97,
Time Complexity: O(N^2)
Auxiliary Space: O(N)