Bellman–Ford Algorithm (original) (raw)

Last Updated : 14 Apr, 2025

Try it on GfG Practice redirect icon

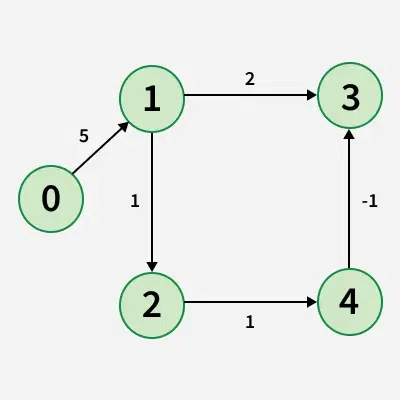
Given a weighted graph with *V vertices and E edges, along with a source vertexsrc*, the task is to compute the shortest distances from the source to all other vertices. If a vertex is unreachable from the source, its distance should be marked as **10 8. In the presence of a negative weight cycle, return -1 to signify that shortest path calculations are not feasible.

**Examples:

**Input: V = 5, edges = [[0, 1, 5], [1, 2, 1], [1, 3, 2], [2, 4, 1], [4, 3, -1]], src = 0

bellman_ford_input_images

**Output: [0, 5, 6, 6, 7]
**Explanation: Shortest Paths:
For 0 to 1 minimum distance will be 5. By following path 0 **→ 1
For 0 to 2 minimum distance will be 6. By following path 0 **→ 1 **→ 2
For 0 to 3 minimum distance will be 6. By following path 0 **→ 1 **→ 2 **→ 4 → 3
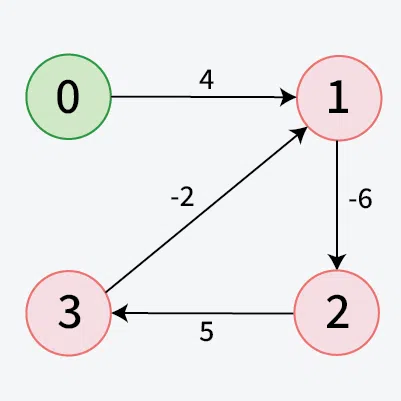
For 0 to 4 minimum distance will be 7. By following path 0 **→ 1 **→ 2 **→ 4

**Input: V = 4, edges = [[0, 1, 4], [1, 2, -6], [2, 3, 5], [3, 1, -2]], src = 0

input-2

**Output: [-1]
**Explanation: The graph contains a negative weight cycle formed by the path **1 → 2 → 3 → 1, where the total weight of the cycle is negative.

Table of Content

Approach: Bellman-Ford Algorithm - O(V*E) Time and O(V) Space

Negative weight cycle:

A negative weight cycle is a cycle in a graph, whose sum of edge weights is negative. If you traverse the cycle, the total weight accumulated would be less than zero.

BellmanFord-Algorithm-eXAMPLE

In the presence of negative weight cycle in the graph, the shortest path **doesn't exist because with each traversal of the cycle shortest path keeps **decreasing.

Limitation of Dijkstra's Algorithm:

Since, we need to find the single source shortest path, we might initially think of using Dijkstra's algorithm. However, Dijkstra is not suitable when the graph consists of **negative edges. The reason is, it **doesn't revisit those nodes which have already been marked as visited. If a shorter path exists through a longer route with negative edges, Dijkstra's algorithm will fail to handle it.

Principle of Relaxation of Edges

**Why Relaxing Edges (V - 1) times gives us Single Source Shortest Path?

A shortest path between two vertices can have at most ****(V - 1)** edges. It is not possible to have a simple path with more than (V - 1) edges (otherwise it would form a cycle). Therefore, repeating the relaxation process (V - 1) times ensures that all possible paths between source and any other node have been covered.

Assuming node **0 as the **source vertex, let's see how we can relax the edges to find the shortest paths:

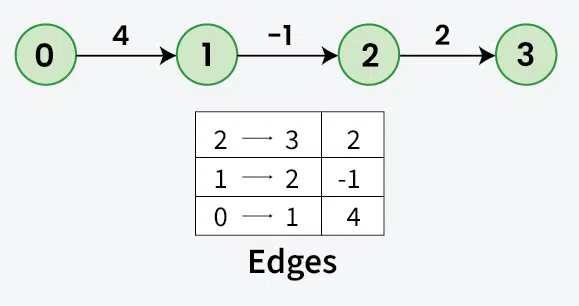
baleman-fort

So, in above example, **dist[1] is updated in **1st relaxation, **dist[2] is updated in **second relaxation, so the dist for the last node (V - 1), will be updated in ****(V - 1) th relaxation**.

Detection of a Negative Weight Cycle

**Bellman-Ford is a **single source shortest path algorithm. It effectively works in the cases of negative edges and is able to detect negative cycles as well. It works on the principle of relaxation of the edges.

**Illustration:

C++ `

#include #include using namespace std;

vector bellmanFord(int V, vector<vector>& edges, int src) {

// Initially distance from source to all 
// other vertices is not known(Infinite).
vector<int> dist(V, 1e8);
dist[src] = 0;

// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (int i = 0; i < V; i++) {
    
    for (vector<int> edge : edges) {
        int u = edge[0];
        int v = edge[1];
        int wt = edge[2];
        if (dist[u] != 1e8 && dist[u] + wt < dist[v]) {
            
            // If this is the Vth relaxation, then there is
            // a negative cycle
            if(i == V - 1)
                return {-1};
           
            // Update shortest distance to node v
            dist[v] = dist[u] + wt;
        }
    }
}

return dist;

}

int main() {

// Number of vertices in the graph
int V = 5;

// Edge list representation: {source, destination, weight}
vector<vector<int>> edges = {
    {1, 3, 2}, 
    {4, 3, -1},
    {2, 4, 1}, 
    {1, 2, 1},
    {0, 1, 5} 
};

// Define the source vertex
int src = 0;

// Run Bellman-Ford algorithm to get shortest paths from src
vector<int> ans = bellmanFord(V, edges, src);

// Output the shortest distances from src to all vertices
for (int dist : ans) 
    cout << dist << " ";

return 0;

}

Java

import java.util.Arrays;

class GfG { static int[] bellmanFord(int V, int[][] edges, int src) {

    // Initially distance from source to all other vertices 
    // is not known(Infinite).
    int[] dist = new int[V];
    Arrays.fill(dist, (int)1e8);
    dist[src] = 0;

    // Relaxation of all the edges V times, not (V - 1) as we  
    // need one additional relaxation to detect negative cycle
    for (int i = 0; i < V; i++) {
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            int wt = edge[2];
            if (dist[u] != 1e8 && dist[u] + wt < dist[v]) {
                
                // If this is the Vth relaxation, then there is
                // a negative cycle
                if (i == V - 1)
                    return new int[]{-1};
                
                // Update shortest distance to node v
                dist[v] = dist[u] + wt;
            }
        }
    }
    return dist;
}

public static void main(String[] args) {
    
// Number of vertices in the graph
int V = 5;

// Edge list representation: {source, destination, weight}
int[][] edges = new int[][] {
    {1, 3, 2},    
    {4, 3, -1},   
    {2, 4, 1},    
    {1, 2, 1},    
    {0, 1, 5}     
};

// Source vertex for Bellman-Ford algorithm
int src = 0;

// Run Bellman-Ford algorithm from the source vertex
int[] ans = bellmanFord(V, edges, src);

// Print shortest distances from the source to all vertices
for (int dist : ans) 
    System.out.print(dist + " ");

} }

Python

def bellmanFord(V, edges, src):

# Initially distance from source to all other vertices 
# is not known(Infinite) e.g. 1e8.
dist = [100000000] * V
dist[src] = 0

# Relaxation of all the edges V times, not (V - 1) as we
# need one additional relaxation to detect negative cycle
for i in range(V):
    for edge in edges:
        u, v, wt = edge
        if dist[u] != 100000000 and dist[u] + wt < dist[v]:
            
            # If this is the Vth relaxation, then there 
            # is a negative cycle
            if i == V - 1:
                return [-1]
            
            # Update shortest distance to node v
            dist[v] = dist[u] + wt
return dist

if name == 'main': V = 5 edges = [[1, 3, 2], [4, 3, -1], [2, 4, 1], [1, 2, 1], [0, 1, 5]]

src = 0
ans = bellmanFord(V, edges, src)
print(' '.join(map(str, ans)))

C#

using System;

class GfG {

// Function to perform the Bellman-Ford algorithm
static int[] bellmanFord(int V, int[,] edges, int src) {
    
    // Initialize distances from source to all
    // vertices as "infinity" (represented by 1e8)
    int[] dist = new int[V];
    for (int i = 0; i < V; i++)
        dist[i] = (int)1e8;

    // Distance to the source is always 0
    dist[src] = 0;

    // Get the number of edges from the 2D edge array
    int E = edges.GetLength(0);

    // Relax all edges V times
    // The extra iteration (V-th) is used to detect a 
    // negative weight cycle
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < E; j++) {

            // Extract edge info: from u to v with weight wt
            int u = edges[j, 0];
            int v = edges[j, 1];
            int wt = edges[j, 2];

            // Only proceed if u has already been reached 
            // (i.e., not infinity)
            if (dist[u] != (int)1e8 && dist[u] + wt < dist[v]) {

                // If this is the V-th iteration and relaxation is still
                // possible, it means there is a negative weight cycle
                if (i == V - 1)
                    // Indicate presence of negative cycle
                    return new int[] { -1 }; 

                // Update the distance to vertex v through vertex u
                dist[v] = dist[u] + wt;
            }
        }
    }

    // Return the final shortest distances
    return dist;
}

static void Main() {
    
    // Number of vertices in the graph
    int V = 5; 

    // Edge list: each row represents {source, destination, weight}
    int[,] edges = {
        { 1, 3, 2 },
        { 4, 3, -1 },
        { 2, 4, 1 },
        { 1, 2, 1 },
        { 0, 1, 5 }
    };

    // Source vertex
    int src = 0; 

    // Call Bellman-Ford and store the result
    int[] ans = bellmanFord(V, edges, src);

    // Print the shortest distances from source to all vertices
    foreach (int d in ans)
        Console.Write(d + " ");
}

}

JavaScript

function bellmanFord(V, edges, src) {

// Initially distance from source to all 
// other vertices is not known(Infinite).
let dist = new Array(V).fill(1e8);
dist[src] = 0;

// Relaxation of all the edges V times, not (V - 1) as we
// need one additional relaxation to detect negative cycle
for (let i = 0; i < V; i++) {
    for (let edge of edges) {
        let u = edge[0];
        let v = edge[1];
        let wt = edge[2];
        if (dist[u] !== 1e8 && dist[u] + wt < dist[v]) {
            
            // If this is the Vth relaxation, then there is
            // a negative cycle
            if (i === V - 1) 
                return [-1];
           
            // Update shortest distance to node v
            dist[v] = dist[u] + wt;
        }
    }
}

return dist;

}

// Driver Code let V = 5; let edges = [ [1, 3, 2], [4, 3, -1], [2, 4, 1], [1, 2, 1], [0, 1, 5] ];

let src = 0; let ans = bellmanFord(V, edges, src); console.log(ans.join(" "));

`

Problems based on Shortest Path