Detect cycle in an undirected graph using BFS (original) (raw)

Last Updated : 04 Apr, 2025

Given an undirected graph, the task is to determine if **cycle is present in it or not.

**Examples:

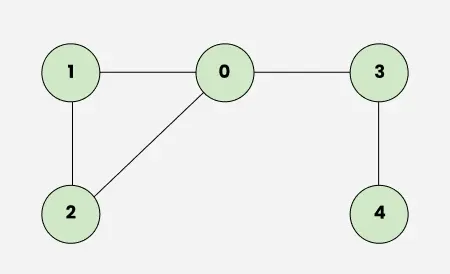
**Input: V = 5, edges[][] = [[0, 1], [0, 2], [0, 3], [1, 2], [3, 4]]

Undirected Graph with 5 Node

**Output: true
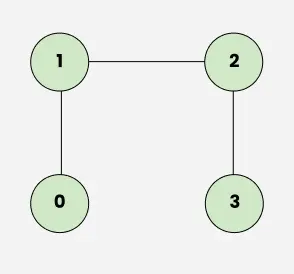
**Explanation: _The diagram clearly shows a cycle 0 → 2 → 1 → 0.

**Input: V = 4, edges[][] = [[0, 1], [1, 2], [2, 3]]

Undirected graph with 4 Node

**Output: false

**Approach:

The idea is to use BFS to detect a cycle in an undirected graph. We start BFS for all components of the graph and check if a node has been visited earlier, ensuring that we **do not consider the parent node of the current node while making this check. If we encounter a visited node that is not the parent, a **cycle exists in the graph. Otherwise, we continue BFS by marking the node as visited and inserting it into the queue.

Step by step approach:

**Initialize a visited array of size n (number of nodes) to false.
**Iterate through all nodes from 0 to n-1. If a node is not visited, start BFS.
**Push the node into the queue with its parent set to -1.
**Perform BFS:
- Pop a node from the queue.
- Traverse all its adjacent nodes.
- If an adjacent node is visited and **is not the parent, return true (cycle detected).
- Otherwise, if the adjacent node is not visited, mark it as visited and push it into the queue with the current node as its parent.
If no cycle is found after checking all components, return false.

**Implementation:

C++ `

#include <bits/stdc++.h> using namespace std;

// Function to perform BFS from node start bool bfs(int start, vector<vector>& adj, vector& visited) { queue<pair<int, int>> q; q.push({start, -1}); visited[start] = true;

while (!q.empty()) {
    int node = q.front().first;
    int parent = q.front().second;
    q.pop();

    for (int neighbor : adj[node]) {

        if (!visited[neighbor]) {
            visited[neighbor] = true;
            q.push({neighbor, node});
        } 
        else if (neighbor != parent) {
            return true;
        }
    }
}
return false;

}

vector<vector> constructadj(int V, vector<vector> &edges){

vector<vector<int>> adj(V);
for (auto it : edges)
{
    adj[it[0]].push_back(it[1]);
    adj[it[1]].push_back(it[0]);
}

return adj;

}

bool isCycle(int V, vector<vector>& edges) {

vector<vector<int>> adj = constructadj(V, edges);
vector<bool> visited(V, false);

for (int i = 0; i < V; i++) {
    
    if (!visited[i]) {
        if (bfs(i, adj, visited)) {
            return true;
        }
    }
}

// If no cycle is found
return false;

}

int main() { vector<vector> edges = {{0, 1}, {0, 2}, {0, 3}, {1, 2}, {3, 4}}; int V = 5;

isCycle(V,edges) ? cout<<"true": cout<<"false";

return 0;

}

Java

import java.util.*;

public class CycleDetection {

// Function to perform BFS from a start node
static boolean bfs(int start, List<Integer>[] adj,
                   boolean[] visited)
{
    Queue<int[]> q = new LinkedList<>();
    q.offer(new int[] { start, -1 });
    visited[start] = true;

    while (!q.isEmpty()) {
        int[] front = q.poll();
        int node = front[0];
        int parent = front[1];

        for (int neighbor : adj[node]) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                q.offer(new int[] { neighbor, node });
            }
            // If visited and not the parent, cycle
            // exists
            else if (neighbor != parent) {
                return true;
            }
        }
    }
    return false;
}
static List<Integer>[] constructadj(int V,
                                    int[][] edges)
{

    List<Integer>[] adj = new ArrayList[V];

    for (int i = 0; i < V; i++) {
        adj[i] = new ArrayList<>();
    }
    for (int[] edge : edges) {
        int u = edge[0], v = edge[1];
        adj[u].add(v);
        adj[v].add(u);
    }

    return adj;
}
static boolean isCycle(int V, int[][] edges)
{
    // Create adjacency list
    List<Integer>[] adj = constructadj(V, edges);
    boolean[] visited = new boolean[V];

    for (int i = 0; i < V; i++) {
        if (!visited[i]) {
            if (bfs(i, adj, visited)) {
                return true;
            }
        }
    }
    return false;
}

public static void main(String[] args)
{
    int[][] edges = {
        {0, 1}, {0, 2}, {0, 3}, {1, 2}, {3, 4}
    };
    int V = 5;
    System.out.println(isCycle(V, edges) ? "true"
                                         : "false");
}

}

Python

from collections import deque

def bfs(start, adj, visited): queue = deque([(start, -1)]) visited[start] = True

while queue:
    node, parent = queue.popleft()

    for neighbor in adj[node]:
        if not visited[neighbor]:
            visited[neighbor] = True
            queue.append((neighbor, node))
        elif neighbor != parent:
            return True
return False

def constructadj(V, edges): adj = [[] for _ in range(V)] # Initialize adjacency list

for edge in edges:
    u, v = edge
    adj[u].append(v)
    adj[v].append(u)

return adj

def iscycle(V, edges): adj = constructadj(V,edges)

visited = [False] * V

for i in range(V):
    if not visited[i]:
        if bfs(i, adj, visited):
            return True

return False

Test the function

edges = [[0, 1], [0, 2], [0, 3], [1, 2], [3, 4]] V = 5 print("true" if iscycle(V, edges) else "false")

C#

using System; using System.Collections.Generic;

class CycleDetection { // Function to perform BFS from a start node static bool Bfs(int start, List[] adj, bool[] visited) { Queue<(int, int)> q = new Queue<(int, int)>(); q.Enqueue((start, -1)); visited[start] = true;

    while (q.Count > 0)
    {
        var (node, parent) = q.Dequeue();

        foreach (int neighbor in adj[node])
        {
            if (!visited[neighbor])
            {
                visited[neighbor] = true;
                q.Enqueue((neighbor, node));
            }
            // If visited and not the parent, cycle exists
            else if (neighbor != parent)
            {
                return true;
            }
        }
    }
    return false;
}

// Function to construct the adjacency list
static List<int>[] constructadj(int V, int[][] edges)
{
    List<int>[] adj = new List<int>[V];

    // Initialize each list in the adjacency list
    for (int i = 0; i < V; i++)
    {
        adj[i] = new List<int>();
    }

    foreach (var edge in edges)
    {
        adj[edge[0]].Add(edge[1]);
        adj[edge[1]].Add(edge[0]);
    }

    return adj;
}

static bool IsCycle(int V, int[][] edges)
{
    // Create adjacency list
    List<int>[] adj = constructadj(V, edges);

    bool[] visited = new bool[V];

    for (int i = 0; i < V; i++)
    {
        if (!visited[i])
        {
            if (Bfs(i, adj, visited))
            {
                return true;
            }
        }
    }
    return false;
}

static void Main()
{
    int[][] edges = new int[][]
    {
        new int[] {0, 1}, new int[] {0, 2}, new int[] {0, 3}, 
        new int[] {1, 2}, new int[] {3, 4}
    };
    int V = 5;
    Console.WriteLine(IsCycle(V, edges) ? "true" : "false");
}

}

JavaScript

function bfs(start, adj, visited) { let queue = [[start, -1]]; visited[start] = true;

while (queue.length > 0) {
    let [node, parent] = queue.shift();

    for (let neighbor of adj[node]) {
        if (!visited[neighbor]) {
            visited[neighbor] = true;
            queue.push([neighbor, node]);
        } else if (neighbor !== parent) {
            return true;
        }
    }
}
return false;

}

function constructadj(V, edges){ let adj = Array.from({length : V}, () => []);

// Build the adjacency list
for (let edge of edges) {
    let [u, v] = edge;
    adj[u].push(v);
    adj[v].push(u);
}
return adj;

}

function isCycle(V, edges) { let adj = constructadj(V,edges);

let visited = Array(V).fill(false);

for (let i = 0; i < V; i++) {
    if (!visited[i]) {
        if (bfs(i, adj, visited)) {
            return true;
        }
    }
}

return false;

}

// Test the function let edges = [[0, 1], [0, 2], [0, 3], [1, 2], [3, 4]]; let V = 5; console.log(isCycle(V, edges) ? "true" : "false");

**Time Complexity: **O(V+E), It visits each node once and processes each edge once using an adjacency list.
**Space Complexity: O(V), O(V) for the queue and visited array.

We do not count the adjacency list in auxiliary space as it is necessary for representing the input graph.

**Related Articles: