Diagonal Traversal of Binary Tree (original) (raw)
Last Updated : 26 Sep, 2024
Given a Binary Tree, the task is to print the **diagonal traversal of the binary tree.
Note: If the diagonal element are present in two different subtrees, then left subtree diagonal element should be taken first and then right subtree.
**Example:
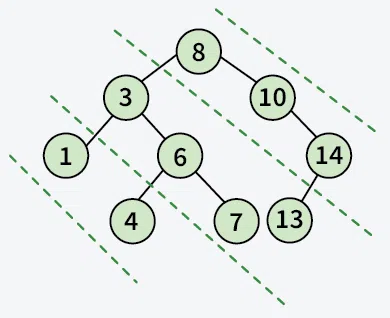
**Input:
**Output: 8 10 14 3 6 7 13 1 4
**Explanation: The above is the diagonal elements in a binary tree that belong to the same line.
Using Recursion and Hashmap - O(n) Time and O(n) Space:
To find the diagonal view of a binary tree, we perform a **recursive traversal that stores nodes in a hashmap based on their diagonal levels. Left children **increase the diagonal level, while **right children remain on the same level.
Below is the implementation of the above approach:
C++ `
// C++ program to print diagonal view #include <bits/stdc++.h> using namespace std;
class Node { public: int data; Node *left, *right; Node(int x) { data = x; left = nullptr; right = nullptr; } };
// Recursive function to print diagonal view void diagonalRecur(Node *root, int level, unordered_map<int, vector> &levelData) {
// Base case
if (root == nullptr)
return;
// Append the current node into hash map.
levelData[level].push_back(root->data);
// Recursively traverse the left subtree.
diagonalRecur(root->left, level + 1, levelData);
// Recursively traverse the right subtree.
diagonalRecur(root->right, level, levelData);}
// function to print diagonal view vector diagonal(Node *root) { vector ans;
// Create a hash map to store each
// node at its respective level.
unordered_map<int, vector<int>> levelData;
diagonalRecur(root, 0, levelData);
int level = 0;
// Insert into answer level by level.
while (levelData.find(level) != levelData.end()) {
vector<int> v = levelData[level];
for (int j = 0; j < v.size(); j++) {
ans.push_back(v[j]);
}
level++;
}
return ans;}
void printList(vector v) { int n = v.size(); for (int i = 0; i < n; i++) { cout << v[i] << " "; } cout << endl; }
int main() {
// Create a hard coded tree
// 8
// / \
// 3 10
// / / \
// 1 6 14
// / \ /
// 4 7 13
Node *root = new Node(8);
root->left = new Node(3);
root->right = new Node(10);
root->left->left = new Node(1);
root->right->left = new Node(6);
root->right->right = new Node(14);
root->right->right->left = new Node(13);
root->right->left->left = new Node(4);
root->right->left->right = new Node(7);
vector<int> ans = diagonal(root);
printList(ans);}
Java
// Java program to print diagonal view import java.util.*;
class Node { int data; Node left, right;
Node(int x) {
data = x;
left = null;
right = null;
}}
class GfG {
// Recursive function to print diagonal view
static void diagonalRecur( Node root, int level,
HashMap<Integer, ArrayList<Integer> > levelData) {
// Base case
if (root == null)
return;
// Append the current node into hash map.
levelData.computeIfAbsent
(level, k -> new ArrayList<>()).add(root.data);
// Recursively traverse the left subtree.
diagonalRecur(root.left, level + 1, levelData);
// Recursively traverse the right subtree.
diagonalRecur(root.right, level, levelData);
}
// function to print diagonal view
static ArrayList<Integer> diagonal(Node root) {
ArrayList<Integer> ans = new ArrayList<>();
// Create a hash map to store each
// node at its respective level.
HashMap<Integer, ArrayList<Integer> > levelData = new HashMap<>();
diagonalRecur(root, 0, levelData);
int level = 0;
// Insert into answer level by level.
while (levelData.containsKey(level)) {
ArrayList<Integer> v = levelData.get(level);
ans.addAll(v);
level++;
}
return ans;
}
static void printList(ArrayList<Integer> v) {
for (int val : v) {
System.out.print(val + " ");
}
System.out.println();
}
public static void main(String[] args) {
// Create a hard coded tree
// 8
// / \
// 3 10
// / / \
// 1 6 14
// / \ /
// 4 7 13
Node root = new Node(8);
root.left = new Node(3);
root.right = new Node(10);
root.left.left = new Node(1);
root.right.left = new Node(6);
root.right.right = new Node(14);
root.right.right.left = new Node(13);
root.right.left.left = new Node(4);
root.right.left.right = new Node(7);
ArrayList<Integer> ans = diagonal(root);
printList(ans);
}}
Python
Python program to print diagonal view
class Node: def init(self, x): self.data = x self.left = None self.right = None
Recursive function to print diagonal view
def diagonalRecur(root, level, levelData):
# Base case
if root is None:
return
# Append the current node into hash map.
if level not in levelData:
levelData[level] = []
levelData[level].append(root.data)
# Recursively traverse the left subtree.
diagonalRecur(root.left, level + 1, levelData)
# Recursively traverse the right subtree.
diagonalRecur(root.right, level, levelData)function to print diagonal view
def diagonal(root): ans = []
# Create a hash map to store each
# node at its respective level.
levelData = {}
diagonalRecur(root, 0, levelData)
level = 0
# Insert into answer level by level.
while level in levelData:
ans.extend(levelData[level])
level += 1
return ansdef printList(v): print(" ".join(map(str, v)))
if name == "main":
# Create a hard coded tree
# 8
# / \
# 3 10
# / / \
# 1 6 14
# / \ /
# 4 7 13
root = Node(8)
root.left = Node(3)
root.right = Node(10)
root.left.left = Node(1)
root.right.left = Node(6)
root.right.right = Node(14)
root.right.right.left = Node(13)
root.right.left.left = Node(4)
root.right.left.right = Node(7)
ans = diagonal(root)
printList(ans)C#
// C# program to print diagonal view using System; using System.Collections.Generic;
class Node { public int data; public Node left, right;
public Node(int x) {
data = x;
left = null;
right = null;
}}
class GfG {
// Recursive function to print diagonal view
static void
DiagonalRecur(Node root, int level,
Dictionary<int, List<int> > levelData) {
// Base case
if (root == null)
return;
// Append the current node into hash map.
if (!levelData.ContainsKey(level)) {
levelData[level] = new List<int>();
}
levelData[level].Add(root.data);
// Recursively traverse the left subtree.
DiagonalRecur(root.left, level + 1, levelData);
// Recursively traverse the right subtree.
DiagonalRecur(root.right, level, levelData);
}
// function to print diagonal view
static List<int> Diagonal(Node root) {
List<int> ans = new List<int>();
// Create a hash map to store each
// node at its respective level.
Dictionary<int, List<int> > levelData
= new Dictionary<int, List<int> >();
DiagonalRecur(root, 0, levelData);
int level = 0;
// Insert into answer level by level.
while (levelData.ContainsKey(level)) {
ans.AddRange(levelData[level]);
level++;
}
return ans;
}
static void PrintList(List<int> v) {
foreach(int i in v) { Console.Write(i + " "); }
Console.WriteLine();
}
static void Main(string[] args) {
// Create a hard coded tree
// 8
// / \
// 3 10
// / / \
// 1 6 14
// / \ /
// 4 7 13
Node root = new Node(8);
root.left = new Node(3);
root.right = new Node(10);
root.left.left = new Node(1);
root.right.left = new Node(6);
root.right.right = new Node(14);
root.right.right.left = new Node(13);
root.right.left.left = new Node(4);
root.right.left.right = new Node(7);
List<int> ans = Diagonal(root);
PrintList(ans);
}}
JavaScript
// JavaScript program to print diagonal view
class Node { constructor(x) { this.key = x; this.left = null; this.right = null; } }
// Recursive function to print diagonal view function diagonalRecur(root, level, levelData) {
// Base case
if (root === null)
return;
// Append the current node into hash map.
if (!levelData[level]) {
levelData[level] = [];
}
levelData[level].push(root.key);
// Recursively traverse the left subtree.
diagonalRecur(root.left, level + 1, levelData);
// Recursively traverse the right subtree.
diagonalRecur(root.right, level, levelData);}
// function to print diagonal view function diagonal(root) { let ans = [];
// Create a hash map to store each
// node at its respective level.
let levelData = {};
diagonalRecur(root, 0, levelData);
let level = 0;
// Insert into answer level by level.
while (level in levelData) {
ans = ans.concat(levelData[level]);
level++;
}
return ans;}
function printList(v) { console.log(v.join(" ")); }
// Create a hard coded tree
// 8
// /
// 3 10
// / /
// 1 6 14
// / \ /
// 4 7 13
let root = new Node(8);
root.left = new Node(3);
root.right = new Node(10);
root.left.left = new Node(1);
root.right.left = new Node(6);
root.right.right = new Node(14);
root.right.right.left = new Node(13);
root.right.left.left = new Node(4);
root.right.left.right = new Node(7);
let ans = diagonal(root); printList(ans);
`
Output
8 10 14 3 6 7 13 1 4
**Time Complexity: O(n), where **n is the number of nodes in the binary tree.
**Auxiliary Space: O(n), used in hash map.
**Note: This approach may get time limit exceeded(TLE) error as it is not an optimized approach. For optimized approach, Please refer to Iterative diagonal traversal of binary tree