Program to Print Fibonacci Series (original) (raw)
Last Updated : 04 Nov, 2024
Ever wondered about the cool math behind the **Fibonacci series? This simple pattern has a remarkable presence in nature, from the arrangement of leaves on plants to the spirals of seashells. We're diving into this **Fibonacci Series sequence. It's not just math, it's in art, nature, and more! Let's discover the secrets of the **Fibonacci series together.
What is the Fibonacci Series?
The Fibonacci series is the sequence where each number is the sum of the previous two numbers of the sequence. The first two numbers of the Fibonacci series are 0 and 1 and are used to generate the Fibonacci series.
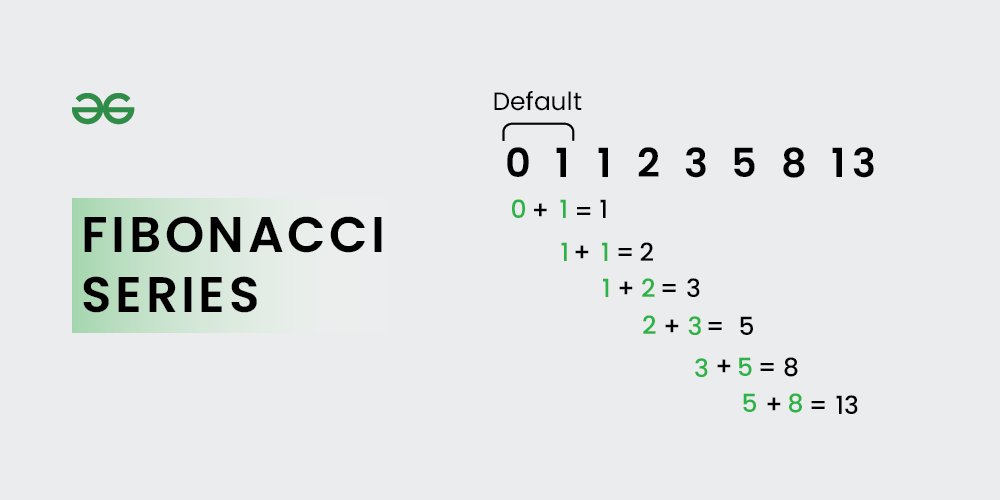
Fibonacci Series
How to Find the Nth term of Fibonacci Series?
In mathematical terms, the number at the **n th position can be represented by:
**Fn = Fn-1 + Fn-2
where, **F 0 = 0 and F 1 = 1.
For example, Fibonacci series 10 terms are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Please refer Different Ways to Find Nth Fibonacci Number for details.
Program to print first N terms of Fibonacci Series:
Given a number n, our task is to print first n terms of the Fibonacci Series.
Input : n = 5
Output : 0 1 1 2 3Input n = 1
Output : 0
We are simply going to run a loop and inside the loop, we are going to keep track of the previous 2 Fibonacci Numbers.
C++ `
// C++ Program to print the fibonacci series // using iteration (loops) #include using namespace std;
// Function to print fibonacci series void printFib(int n) { if (n < 1) { cout << "Invalid Number of terms\n"; return; }
// When number of terms is greater than 0
int prev1 = 1;
int prev2 = 0;
cout << prev2 << " ";
// If n is 1, then we do not need to
// proceed further
if (n == 1)
return;
cout << prev1 << " ";
// Print 3rd number onwards using
// the recursive formula
for (int i = 3; i <= n; i++)
{
int curr = prev1 + prev2;
prev2 = prev1;
prev1 = curr;
cout << curr << " ";
}}
// Driver code int main() { int n = 9; printFib(n); return 0; }
C
#include <stdio.h>
// Function to print fibonacci series void printFib(int n) { if (n < 1) { printf("Invalid Number of terms\n"); return; }
// When number of terms is greater than 0
int prev1 = 1;
int prev2 = 0;
printf("%d ", prev2);
// If n is 1, then we do not need to
// proceed further
if (n == 1)
return;
printf("%d ", prev1);
// Print 3rd number onwards using
// the recursive formula
for (int i = 3; i <= n; i++) {
int curr = prev1 + prev2;
prev2 = prev1;
prev1 = curr;
printf("%d ", curr);
}}
// Driver code int main() { int n = 9; printFib(n); return 0; }
Java
class GfG {
// Function to print fibonacci series
static void printFib(int n) {
if (n < 1) {
System.out.println("Invalid Number of terms");
return;
}
// When number of terms is greater than 0
int prev1 = 1;
int prev2 = 0;
System.out.print(prev2 + " ");
// If n is 1, then we do not need to
// proceed further
if (n == 1)
return;
System.out.print(prev1 + " ");
// Print 3rd number onwards using
// the recursive formula
for (int i = 3; i <= n; i++) {
int curr = prev1 + prev2;
prev2 = prev1;
prev1 = curr;
System.out.print(curr + " ");
}
}
// Driver code
public static void main(String[] args) {
int n = 9;
printFib(n);
}}
Python
Function to print fibonacci series
def print_fib(n): if n < 1: print("Invalid Number of terms") return
# When number of terms is greater than 0
prev1 = 1
prev2 = 0
print(prev2, end=" ")
# If n is 1, then we do not need to
# proceed further
if n == 1:
return
print(prev1, end=" ")
# Print 3rd number onwards using
# the recursive formula
for i in range(3, n + 1):
curr = prev1 + prev2
prev2 = prev1
prev1 = curr
print(curr, end=" ")Driver code
if name == "main": n = 9 print_fib(n)
C#
using System;
class GfG { // Function to print fibonacci series static void printFib(int n) { if (n < 1) { Console.WriteLine("Invalid Number of terms"); return; }
// When number of terms is greater than 0
int prev1 = 1;
int prev2 = 0;
Console.Write(prev2 + " ");
// If n is 1, then we do not need to
// proceed further
if (n == 1)
return;
Console.Write(prev1 + " ");
// Print 3rd number onwards using
// the recursive formula
for (int i = 3; i <= n; i++)
{
int curr = prev1 + prev2;
prev2 = prev1;
prev1 = curr;
Console.Write(curr + " ");
}
}
// Driver code
static void Main(string[] args)
{
int n = 9;
printFib(n);
}}
JavaScript
// Function to print fibonacci series function printFib(n) { if (n < 1) { console.log("Invalid Number of terms"); return; }
// When number of terms is greater than 0
let prev1 = 1;
let prev2 = 0;
process.stdout.write(prev2 + " ");
// If n is 1, then we do not need to
// proceed further
if (n == 1) return;
process.stdout.write(prev1 + " ");
// Print 3rd number onwards using
// the recursive formula
for (let i = 3; i <= n; i++) {
let curr = prev1 + prev2;
prev2 = prev1;
prev1 = curr;
process.stdout.write(curr + " ");
}}
// Driver code let n = 9; printFib(n);
`
Output
0 1 1 2 3 5 8 13 21
Complexity Analysis
- **Time Complexity: O(n)
- **Auxiliary Space: O(1)
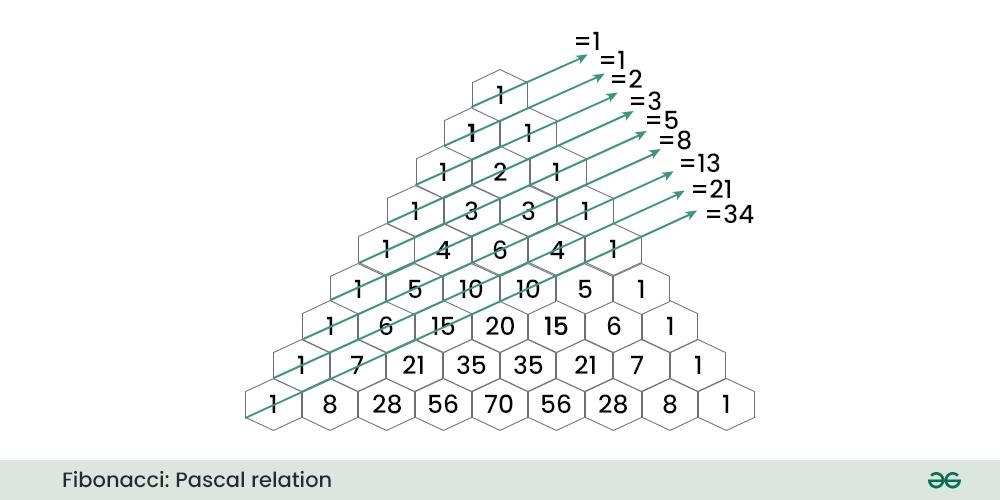
Relation Between Pascal triangle and Fibonacci numbers:
Pascal’s triangle is the arrangement of the data in triangular form which is used to represent the coefficients of the binomial expansions, i.e. the second row in Pascal’s triangle represents the coefficients in (x+y)2 and so on. In Pascal’s triangle, each number is the sum of the above two numbers. Pascal’s triangle has various applications in probability theory, combinatorics, algebra, and various other branches of mathematics.
As shown in the image the **diagonal sum of the **pascal's triangle forms a fibonacci sequence.
**Mathematically: \Sigma_{k=0}^{\left \lfloor n/2 \right \rfloor} \binom{n-k}{k} = F_{n+1}
where F_{t} is the t-th term of the Fibonacci sequence.
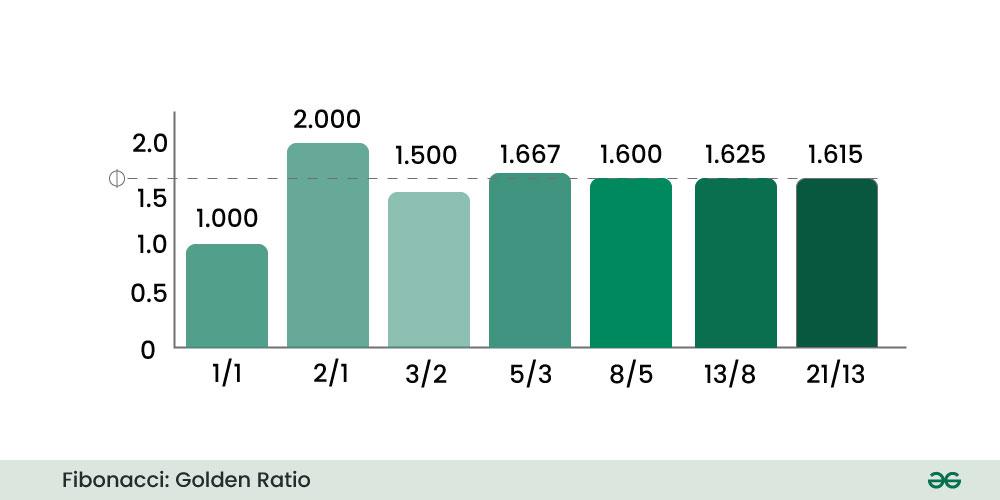
Golden Ratio:
**Definition: The golden ratio, often denoted by the Greek letter phi (**Φ) or the mathematical symbol **τ (tau), is a special mathematical constant that has been of interest to mathematicians, scientists, artists, and architects for centuries. It is an irrational number, meaning its decimal representation goes on forever without repeating, and it is approximately equal to 1.6180339887...
The below image shows how the division of consecutive Fibonacci number forms a **Golden Ratio i.e,
- **x-axis : F(n+1)/F(n), where F( ) represents a Fibonacci number.
- **y-axis : represents the value of the fraction obtained in x-axis.
The ratio of successive Fibonacci numbers approximates the **golden ratio, and this relationship becomes more accurate as you move further along the Fibonacci sequence.
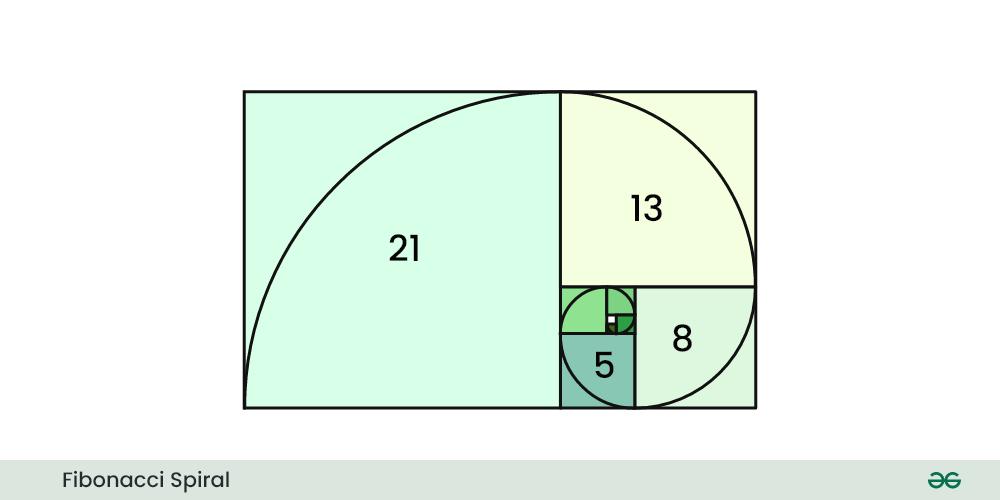
**Fibonacci Spiral:
The Fibonacci spiral is created using a series of quarter circles, with radii that correspond to the Fibonacci numbers as shown in below image:
The resulting spiral is known as a "**Fibonacci spiral" or a "**Golden Spiral" It is often associated with the **Golden Ratio, which is an irrational number approximately equal to **1.61803398875. The Fibonacci spiral is considered visually pleasing and can be found in various aspects of art, architecture, and nature due to its aesthetic qualities and mathematical significance.
Problems based on Fibonacci Number/Series:
- Sum of Fibonacci Numbers
- How to check if a given number is Fibonacci number?
- Program to print first n Fibonacci Numbers
- Program to print Fibonacci Triangle
- Minimum Fibonacci terms with sum equal to K
- Largest subset whose all elements are Fibonacci numbers
- Tiling Problem
- Fibonacci Search
- Matrix Exponentiation
- Count Possible Decodings of a given Digit Sequence
- Count number of binary strings without consecutive 1’s
- Find nth Fibonacci number using Golden ratio
- Maximum games played by winner
- Count possible ways to construct buildings
- Find two Fibonacci numbers whose sum can be represented as N
- Minimum number of Fibonacci jumps to reach end
Some Facts about Fibonacci Numbers:
- The Fibonacci numbers were first mentioned in **Indian mathematics in a work by **Pingala on enumerating potential patterns of **Sanskrit poetry built from syllables of two lengths. The numbers were named after the **Italian mathematician **Leonardo of Pisa, also known as Fibonacci.
- The Fibonacci sequence and the golden ratio are often found in natural patterns, such as the arrangement of leaves on a stem, the spirals of a pinecone, the seeds in a sunflower, and in art and architecture, like the Parthenon in Athens.
- **November 23 is Fibonacci Day as it forms the first **4 digits of fibonacci numbers **11/23.
- Honey bees' family tree follows fibonacci sequence.
Applications of Fibonacci Number/Series:
- **Mile to kilometre approximation : If a distance in miles is a fibonacci number then the succeeding fibonacci number is its kilmometer representation. Example: If we take a number from Fibonacci series i.e., 13 then the kilometre value will be 20.9215 by formulae, which is nearly 21 by rounding.
- **Financial Analysis: In the field of technical analysis in finance, **Fibonacci retracement is a popular tool used to identify potential levels of support and resistance in stock and commodity price charts.
- **Art and Design: The golden ratio, which is closely related to Fibonacci numbers, is often used in art and design to create aesthetically pleasing proportions and layouts. It can be seen in architecture, paintings, and sculptures.
- **Data Structures and Algorithms: Fibonacci heaps, a type of data structure in computer science, are used in certain algorithms, such as Dijkstra's algorithm, for efficient graph processing.