Floyd Warshall Algorithm (original) (raw)

Last Updated : 16 Apr, 2025

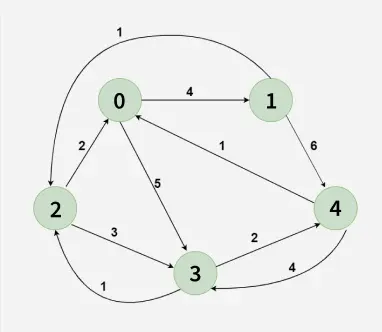
Given a matrix dist[][] of size n x n, where dist[i][j] represents the weight of the edge from node i to node j. If there is no direct edge, dist[i][j] is set to a large value (e.g., 10⁸) to represent infinity. The diagonal entries dist[i][i] are 0, since the distance from a node to itself is zero. The graph **may contain negative edge weights, but it **does not contain any negative weight cycles.

Your task is to determine the shortest path distance between all pair of nodesi** and **j**in the graph.

**Example:

**Input: dist[][] = [[0, 4, 10⁸, 5, 10⁸],
[10⁸, 0, 1, 10⁸, 6],
[2, 10⁸, 0, 3, 10⁸],
[10⁸, 10⁸, 1, 0, 2],
[1, 10⁸, 10⁸, 4, 0]]

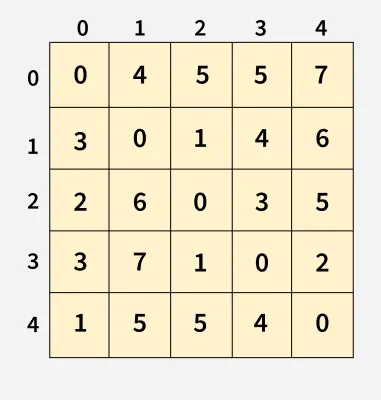
****Output:**[[0, 4, 5, 5, 7],
[3, 0, 1, 4, 6],
[2, 6, 0, 3, 5],
[3, 7, 1, 0, 2],
[1, 5, 5, 4, 0]]
**Explanation:

Each cell dist[i][j] in the output shows the shortest distance from node i to node j, computed by considering all possible intermediate nodes using the Floyd-Warshall algorithm.

Floyd Warshall Algorithm:

The **Floyd–Warshall algorithm works by maintaining a two-dimensional array that represents the distances between nodes. Initially, this array is filled using only the direct edges between nodes. Then, the algorithm gradually updates these distances by checking if shorter paths exist through intermediate nodes.

This algorithm works for both the **directed and **undirected weighted graphs and can handle graphs with both **positive and **negative weight edges.

**Note: It does not work for the graphs with negative cycles (where the sum of the edges in a cycle is negative).

Idea Behind Floyd Warshall Algorithm:

Suppose we have a graph dist**[][] with **V vertices from 0 to **V-1. Now we have to evaluate a **dist[][] where **dist[i][j] represents the shortest path between vertex **i to **j.

Let us assume that vertices **i to **j have intermediate nodes. The idea behind Floyd Warshall algorithm is to treat each and every vertex k from **0 to **V-1 as an intermediate node one by one. When we consider the vertex k, we must have considered vertices from 0 to k-1 already. So we use the shortest paths built by previous vertices to build shorter paths with vertex k included.

The following figure shows the above optimal substructure property in Floyd Warshall algorithm:

**Why Floyd Warshall Works (Correctness Proof)?

The algorithm relies on the **principle of optimal substructure, meaning:

If the shortest path from i to j passes through some vertex k, then the path from i to k and the path from k to j must also be shortest paths.
The iterative approach ensures that by the time vertex k is considered, all shortest paths using only vertices 0 to k-1 have already been computed.

By the end of the algorithm, all shortest paths are computed optimally because each possible intermediate vertex has been considered.

Why Floyd-Warshall Algorithm better for Dense Graphs and not for Sparse Graphs?

**Dense Graph: A graph in which the number of edges are significantly much higher than the number of vertices.
**Sparse Graph: A graph in which the number of edges are very much low.

No matter how many edges are there in the graph the **Floyd Warshall Algorithm runs for O(V3) times therefore it is best suited for **Dense graphs. In the case of sparse graphs, **Johnson's Algorithm is more suitable.

**Step-by-step implementation

**Start by updating the distance matrix by treating each vertex as a possible intermediate node between all pairs of vertices.
**Iterate through each vertex, one at a time. For each selected vertex k, attempt to improve the shortest paths that pass through it.
When we pick vertex number **k as an intermediate vertex, we already have considered vertices ****{0, 1, 2, .. k-1}** as intermediate vertices.
For every pair (i, j) of the source and destination vertices respectively, there are two possible cases.
- **k is not an intermediate vertex in shortest path from i to j. We keep the value of dist[i][j] as it is.
- **k is an intermediate vertex in shortest path from **i to j. We update the value of dist[i][j] as **dist[i][k] + dist[k][j], if **dist[i][j] > dist[i][k] + dist[k][j]
Repeat this process for each vertex k until all intermediate possibilities have been considered.

**Illustration:

C++ `

#include #include #include using namespace std;

// Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(vector<vector> &dist) { int V = dist.size();

// Add all vertices one by one to
// the set of intermediate vertices.
for (int k = 0; k < V; k++) {

    // Pick all vertices as source one by one
    for (int i = 0; i < V; i++) {

        // Pick all vertices as destination
        // for the above picked source
        for (int j = 0; j < V; j++) {

            // shortest path from
            // i to j 
            if(dist[i][k] != 1e8 && dist[k][j]!= 1e8)
            dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);
        }
    }
}

}

int main() { int INF = 100000000; vector<vector> dist = { {0, 4, INF, 5, INF}, {INF, 0, 1, INF, 6}, {2, INF, 0, 3, INF}, {INF, INF, 1, 0, 2}, {1, INF, INF, 4, 0} };

floydWarshall(dist);
for(int i = 0; i<dist.size(); i++) {
    for(int j = 0; j<dist.size(); j++) {
        cout<<dist[i][j]<<" ";
    }
    cout<<endl;
}
return 0;

}

Java

import java.util.*;

class GfG {

// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
static void floydWarshall(int[][] dist){
    int V = dist.length;

    // Add all vertices one by one to
    // the set of intermediate vertices.
    for (int k = 0; k < V; k++) {

        // Pick all vertices as source one by one
        for (int i = 0; i < V; i++) {

            // Pick all vertices as destination
            // for the above picked source
            for (int j = 0; j < V; j++) {

                // shortest path from
                // i to j 
                if(dist[i][k] != 1e8 && dist[k][j]!= 1e8)
                dist[i][j] = Math.min(dist[i][j],dist[i][k] + dist[k][j]);
            }
        }
    }
}

public static void main(String[] args)
{
    int INF = 100000000;

    int[][] dist = { { 0, 4, INF, 5, INF },
                     { INF, 0, 1, INF, 6 },
                     { 2, INF, 0, 3, INF },
                     { INF, INF, 1, 0, 2 },
                     { 1, INF, INF, 4, 0 } };

    floydWarshall(dist);
    for (int i = 0; i < dist.length; i++) {
        for (int j = 0; j < dist.length; j++) {
            System.out.print(dist[i][j] + " ");
        }
        System.out.println();
    }
}

}

Python

Solves the all-pairs shortest path

problem using Floyd Warshall algorithm

def floydWarshall(dist): V = len(dist)

# Add all vertices one by one to
# the set of intermediate vertices.
for k in range(V):

    # Pick all vertices as source one by one
    for i in range(V):

        # Pick all vertices as destination
        # for the above picked source
        for j in range(V):
            #shortest path from
            #i to j 
            if(dist[i][k] != 100000000 and dist[k][j]!= 100000000):
                dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);

if name == "main":

INF = 100000000;
dist = [
    [0, 4, INF, 5, INF],
    [INF, 0, 1, INF, 6],
    [2, INF, 0, 3, INF],
    [INF, INF, 1, 0, 2],
    [1, INF, INF, 4, 0]
]

floydWarshall(dist)
for i in range(len(dist)):
    for j in range(len(dist)):
        print(dist[i][j], end=" ")
    print()

C#

using System;

class GfG { static void floydWarshall(int[,] dist) { int V = dist.GetLength(0);

    for (int k = 0; k < V; k++)
    {
        for (int i = 0; i < V; i++)
        {
            for (int j = 0; j < V; j++)
            {
                // shortest path from
                // i to j 
            if(dist[i,k] != 1e8 && dist[k, j]!= 1e8)
               dist[i,j] = Math.Min(dist[i, j], dist[i, k] + dist[k, j]);
            }
        }
    }
}
// large number as "infinity"
const int INF = 100000000; 

static void Main()
{
    int[,] dist = {
        {0, 4, INF, 5, INF},
        {INF, 0, 1, INF, 6},
        {2, INF, 0, 3, INF},
        {INF, INF, 1, 0, 2},
        {1, INF, INF, 4, 0}
    };

    floydWarshall(dist);

    for (int i = 0; i < dist.GetLength(0); i++)
    {
        for (int j = 0; j < dist.GetLength(1); j++)
        {
                Console.Write(dist[i, j] + " ");
        }
        Console.WriteLine();
    }
}

}

JavaScript

// Solves the all-pairs shortest path // problem using Floyd Warshall algorithm function floydWarshall(dist) { let V = dist.length;

// Add all vertices one by one to
// the set of intermediate vertices.
for (let k = 0; k < V; k++) {

    // Pick all vertices as source one by one
    for (let i = 0; i < V; i++) {

        // Pick all vertices as destination
        // for the above picked source
        for (let j = 0; j < V; j++) {

            // shortest path from
            // i to j
            if (dist[i][k] != INF && dist[k][j] != INF) {
                dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
            }
        }
    }
}

}

let INF = 100000000;

// Driver Code let dist = [ [0, 4, INF, 5, INF], [INF, 0, 1, INF, 6], [2, INF, 0, 3, INF], [INF, INF, 1, 0, 2], [1, INF, INF, 4, 0] ];

floydWarshall(dist);

for (let i = 0; i < dist.length; i++) { console.log(dist[i].join(" ")); }

Output

0 4 5 5 7 3 0 1 4 6 2 6 0 3 5 3 7 1 0 2 1 5 5 4 0

**Time Complexity: O(V3), where V is the number of vertices in the graph and we run three nested loops each of size V.
**Auxiliary Space: O(1).

**Read here for detailed analysis: complexity analysis of the Floyd Warshall algorithm

**Note: The above program only prints the shortest distances. We can modify the solution to print the shortest paths also by storing the predecessor information in a separate 2D matrix.

Real World Applications of Floyd-Warshall Algorithm

In computer networking, the algorithm can be used to find the shortest path between all pairs of nodes in a network. This is termed as **network routing.
Flight Connectivity In the aviation industry to find the shortest path between the airports.
**GIS(**Geographic Information Systems) applications often involve analyzing spatial data, such as road networks, to find the shortest paths between locations.
Kleene's algorithm which is a generalization of floyd warshall, can be used to find regular expression for a regular language.