Level of a Node in Binary Tree (original) (raw)

Last Updated : 29 Sep, 2024

Try it on GfG Practice

Given a **Binary Tree and a **key, the task is to find the **level of key in the Binary Tree.

**Examples:

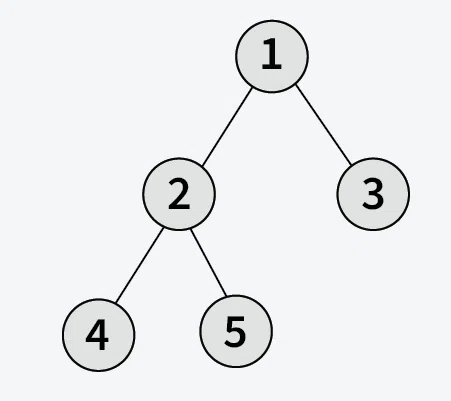
**Input : key = 4

**Output: 3
**Explanation: The level of the key in above binary tree is 3.

**Input : key = 10

**Output: -1
**Explanation: Key is not present in the above Binary tree.

Table of Content

• [Expected Approach - 1] Using Recursion - O(n) Time and O(h) Space
• [Expected Approach - 2] Using Level Order Traversal- O(n) Time and O(n) Space

**[Expected Approach - 1] Using Recursion - O(n) Time and O(h) Space

The idea is to start from the **root and level as 1. If the target matches with root's data, return **level. Else **recursively call for left and right subtrees with level as **level + 1.

Below is the implementation of the above approach:

C++ `

// C++ code to find level of a Node in Binary Tree

#include using namespace std;

class Node { public: int data; Node* left; Node* right;

Node(int val) {
    data = val;
    left = right = nullptr;
}

};

// Recursive function to find the level of the target key int getLevel(Node* root, int target, int level) { if (root == nullptr) { return -1; }

// If the target key matches the current node's 
  // data, return the level
if (root->data == target) {
    return level;
}

// Recursively call for left and right subtrees
int leftLevel = getLevel(root->left, target, level + 1);
if (leftLevel != -1) {
    return leftLevel;
}

return getLevel(root->right, target, level + 1);

}

int main() {

// Creating a sample binary tree:
//       1
//      / \
//     2   3
//    / \ / \
//   4  5 6  7
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);

int target = 5;
cout << getLevel(root, target, 1) << endl;

return 0;

}

C

// C code to find level of a Node in Binary Tree

#include <stdio.h> #include <stdlib.h>

struct Node { int data; struct Node* left; struct Node* right; };

int getLevel(struct Node* root, int target, int level) { if (root == NULL) { return -1; }

// If the target key matches the current node's data, return the level
if (root->data == target) {
    return level;
}

// Recursively call for left and right subtrees
int leftLevel = getLevel(root->left, target, level + 1);
if (leftLevel != -1) {
    return leftLevel;
}

return getLevel(root->right, target, level + 1);

}

struct Node* createNode(int val) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = val; newNode->left = newNode->right = NULL; return newNode; }

int main() {

// Creating a sample binary tree:
//       1
//      / \
//     2   3
//    / \ / \
//   4  5 6  7
struct Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);

int target = 5;
printf("%d\n", getLevel(root, target, 1));

return 0;

}

Java

// Java code to find level of a Node in Binary Tree

class Node { int data; Node left, right;

Node(int val) {
    data = val;
    left = right = null;
}

}

class GfG {

// Recursive function to find the level of the target key
static int getLevel(Node root, int target, int level) {
    if (root == null) {
        return -1;
    }

    // If the target key matches the current node's 
      // data, return the level
    if (root.data == target) {
        return level;
    }

    // Recursively call for left and right subtrees
    int leftLevel = getLevel(root.left, target, level + 1);
    if (leftLevel != -1) {
        return leftLevel;
    }

    return getLevel(root.right, target, level + 1);
}

public static void main(String[] args) {
  
    // Creating a sample binary tree:
    //       1
    //      / \
    //     2   3
    //    / \ / \
    //   4  5 6  7
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.left = new Node(6);
    root.right.right = new Node(7);

    int target = 5;
    System.out.println(getLevel(root, target, 1));
}

}

Python

Python code to find level of a Node in Binary Tree

class Node: def init(self, val): self.data = val self.left = None self.right = None

Recursive function to find the level of the target key

def getLevel(root, target, level): if root is None: return -1

# If the target key matches the current node's
# data, return the level
if root.data == target:
    return level

# Recursively call for left and right subtrees
leftLevel = getLevel(root.left, target, level + 1)
if leftLevel != -1:
    return leftLevel

return getLevel(root.right, target, level + 1)

if name == "main":

# Creating a sample binary tree:
#       1
#      / \
#     2   3
#    / \ / \
#   4  5 6  7
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)

target = 5
print(getLevel(root, target, 1))

C#

// C# code to find level of a Node in Binary Tree

using System;

class Node { public int Data; public Node Left; public Node Right;

public Node(int val) {
    Data = val;
    Left = Right = null;
}

}

class GfG {

// Recursive function to find the level of the target key
static int GetLevel(Node root, int target, int level) {
    if (root == null) {
        return -1;
    }

    // If the target key matches the current
      // node's data, return the level
    if (root.Data == target) {
        return level;
    }

    // Recursively call for left and right subtrees
    int leftLevel = GetLevel(root.Left, target, level + 1);
    if (leftLevel != -1) {
        return leftLevel;
    }

    return GetLevel(root.Right, target, level + 1);
}

static void Main() {
  
    // Creating a sample binary tree:
    //       1
    //      / \
    //     2   3
    //    / \ / \
    //   4  5 6  7
    Node root = new Node(1);
    root.Left = new Node(2);
    root.Right = new Node(3);
    root.Left.Left = new Node(4);
    root.Left.Right = new Node(5);
    root.Right.Left = new Node(6);
    root.Right.Right = new Node(7);

    int target = 5;
    Console.WriteLine(GetLevel(root, target, 1));
}

}

JavaScript

// Javascript code to find level of a Node // in Binary Tree

class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } }

// Recursive function to find the level of the target key function getLevel(root, target, level) { if (root === null) { return -1; }

// If the target key matches the current node's
// data, return the level
if (root.data === target) {
    return level;
}

// Recursively call for left and right subtrees
let leftLevel = getLevel(root.left, target, level + 1);
if (leftLevel !== -1) {
    return leftLevel;
}

return getLevel(root.right, target, level + 1);

}

// Creating a sample binary tree: // 1 // /
// 2 3 // / \ /
// 4 5 6 7 const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7);

const target = 5; console.log(getLevel(root, target, 1));

`

**Time Complexity: O(n), where **n is the number of nodes in the binary tree.
**Auxiliary Space: O(h), where **h is height of binary tree.

**[Expected Approach - 2] Using Level Order Traversal- O(n) Time and O(n) Space

The idea is to perform a level-order traversal and keep track of the **current level as we traverse the tree. If the **key matches with root's data, return level.

C++ `

// C++ code to find level of a Node in Binary Tree

#include <bits/stdc++.h> using namespace std;

class Node { public: int data; Node* left; Node* right;

Node(int val) {
    data = val;
    left = right = nullptr;
}

};

// Function to find the level of the target key int getLevel(Node* root, int target) { if (root == nullptr) { return -1; }

// Create a queue for level-order 

// traversal queue<Node*> q; q.push(root); int level = 1;

while (!q.empty()) {
    int size = q.size();

    // Process all nodes at the current level
    for (int i = 0; i < size; i++) {
        Node* curr = q.front();
        q.pop();

        // Check if the current node matches the target
        if (curr->data == target) {
            return level;
        }

        // Push the left and right children to the queue
        if (curr->left != nullptr) {
            q.push(curr->left);
        }
        if (curr->right != nullptr) {
            q.push(curr->right);
        }
    }

    level++;
}

return -1;

}

int main() {

// Creating a sample binary tree:
//       1
//      / \
//     2   3
//    / \ / \
//   4  5 6  7
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);

int target = 5;
cout << getLevel(root, target);

return 0;

}

Java

// Java code to find level of a Node // in Binary Tree

import java.util.LinkedList; import java.util.Queue;

class Node { int data; Node left, right;

Node(int val) {
    data = val;
    left = right = null;
}

}

// Function to find the level of // the target key class GfG {

static int getLevel(Node root, int target) {
    if (root == null) {
        return -1;
    }

    // Create a queue for level-order traversal
    Queue<Node> q = new LinkedList<>();
    q.add(root);
    int level = 1;

    while (!q.isEmpty()) {
        int size = q.size();

        // Process all nodes at the current level
        for (int i = 0; i < size; i++) {
            Node curr = q.poll();

            // Check if the current node matches the target
            if (curr.data == target) {
                return level;
            }

            // Push the left and right children to the queue
            if (curr.left != null) {
                q.add(curr.left);
            }
            if (curr.right != null) {
                q.add(curr.right);
            }
        }
      
        level++;
    }
  
    return -1;
}

public static void main(String[] args) {
      
    // Creating a sample binary tree:
    //       1
    //      / \
    //     2   3
    //    / \ / \
    //   4  5 6  7
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.left = new Node(6);
    root.right.right = new Node(7);

    int target = 5;
    System.out.println(getLevel(root, target));
}

}

Python

Python code to find level of a Node in Binary Tree

class Node: def init(self, val): self.data = val self.left = None self.right = None

Function to find the level of the target key

def getLevel(root, target): if root is None: return -1

# Create a queue for level-order traversal
q = []
q.append(root)
level = 1

while len(q) > 0:
    size = len(q)

    # Process all nodes at the current level
    for i in range(size):
        curr = q.pop(0)

        # Check if the current node matches the target
        if curr.data == target:
            return level

        # Push the left and right children to the queue
        if curr.left is not None:
            q.append(curr.left)
        if curr.right is not None:
            q.append(curr.right)

    level += 1
    
return -1

if name == "main":

# Creating a sample binary tree:
#       1
#      / \
#     2   3
#    / \ / \
#   4  5 6  7
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)

target = 5
print(getLevel(root, target))

C#

// C# code to find level of a Node in Binary Tree

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int val) {
    data = val;
    left = right = null;
}

}

class GfG {

// Function to find the level of the target key
static int GetLevel(Node root, int target) {
    if (root == null) {
        return -1;
    }

    // Create a queue for level-order traversal
    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);
    int level = 1;

    while (q.Count > 0) {
        int size = q.Count;

        // Process all nodes at the current level
        for (int i = 0; i < size; i++) {
            Node curr = q.Dequeue();

            // Check if the current node matches the target
            if (curr.data == target) {
                return level;
            }

            // Push the left and right children to the queue
            if (curr.left != null) {
                q.Enqueue(curr.left);
            }
            if (curr.right != null) {
                q.Enqueue(curr.right);
            }
        }

        level++;
    }
  
    return -1;
}

static void Main(string[] args) {
      
    // Creating a sample binary tree:
    //       1
    //      / \
    //     2   3
    //    / \ / \
    //   4  5 6  7
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.left = new Node(6);
    root.right.right = new Node(7);

    int target = 5;
    Console.WriteLine(GetLevel(root, target));
}

}

JavaScript

// Javascript code to find level of // a Node in Binary Tree

class Node { constructor(val) { this.data = val; this.left = this.right = null; } }

// Function to find the level of the target key function getLevel(root, target) { if (root === null) { return -1; }

// Create a queue for level-order traversal
let q = [];
q.push(root);
let level = 1;

while (q.length > 0) {
    let size = q.length;

    // Process all nodes at the current level
    for (let i = 0; i < size; i++) {
        let curr = q.shift();

        // Check if the current node matches the target
        if (curr.data === target) {
            return level;
        }

        // Push the left and right children to the queue
        if (curr.left !== null) {
            q.push(curr.left);
        }
        if (curr.right !== null) {
            q.push(curr.right);
        }
    }
    
    level++;
} 

return -1;

}

// Creating the binary tree // 1 // /
// 2 3 // / \ /
// 4 5 6 7 let root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7);

let target = 5; console.log(getLevel(root, target));

`

**Time Complexity: O(n), where n is the number of nodes in the binary tree.
**Auxiliary Space: O(n)