Inorder Traversal of Binary Tree (original) (raw)

Last Updated : 28 Mar, 2025

Inorder traversal is a **depth-first traversal method that follows this sequence:

**Left subtree is visited first.
**Root node is processed next.
**Right subtree is visited last.

How does Inorder Traversal work?

**Key Properties:

If applied to a **Binary Search Tree (BST), it **returns elements in sorted order.
Ensures that nodes are **processed in a hierarchical sequence, making it useful for expression trees and BSTs.

Examples

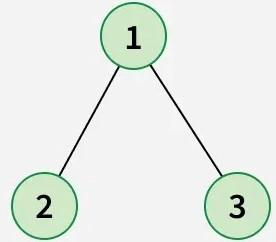
**Input:

**Output: 2 1 3
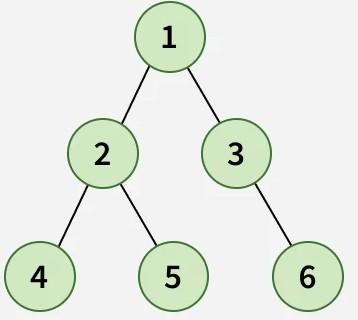
**Explanation: The Inorder Traversal visits the nodes in the following order: Left, Root, Right. Therefore, we visit the left node 2, then the root node 1 and lastly the right node 3.

**Input :

Output: 4 2 5 1 3 6
Explanation: Inorder Traversal (Left → Root → Right).** Visit 4 → 2 → 5 → 1 → 3 → 6 , resulting in 4 2 5 1 3 6.

Algorithm :

If the root is NULL, return.

Recursively traverse the left subtree.

Process the root node (e.g., print its value).

Recursively traverse the right subtree.

C++ `

#include <bits/stdc++.h> using namespace std;

// Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; Node(int v) { data = v; left = right = nullptr; } };

// Function to print inorder traversal void printInorder(struct Node* node) { if (node == nullptr) return;

// First recur on left subtree
printInorder(node->left);

// Now deal with the node
cout << node->data << " ";

// Then recur on right subtree
printInorder(node->right);

}

int main() { struct Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->right = new Node(6);

printInorder(root);

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

// Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; };

// Function to print inorder traversal void printInorder(struct Node* node) { if (node == NULL) return;

// First recur on left subtree
printInorder(node->left);

// Now deal with the node
printf("%d ", node->data);

// Then recur on right subtree
printInorder(node->right);

}

// Function to create a new node struct Node* newNode(int v) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = v; node->left = node->right = NULL; return node; }

int main() { struct Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); root->right->right = newNode(6);

printInorder(root);

return 0;

}

Java

import java.util.*;

// Structure of a Binary Tree Node class Node { int data; Node left, right;

Node(int v)
{
    data = v;
    left = right = null;
}

}

class GfG { // Function to print inorder traversal public static void printInorder(Node node) { if (node == null) return;

    // First recur on left subtree
    printInorder(node.left);

    // Now deal with the node
    System.out.print(node.data + " ");

    // Then recur on right subtree
    printInorder(node.right);
}

public static void main(String[] args)
{
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    printInorder(root);
}

}

Python

class Node: def init(self, v): self.data = v self.left = None self.right = None

Function to print inorder traversal

def printInorder(node): if node is None: return

# First recur on left subtree
printInorder(node.left)

# Now deal with the node
print(node.data, end=' ')

# Then recur on right subtree
printInorder(node.right)

if name == 'main': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.right = Node(6)

printInorder(root)

C#

using System;

// Structure of a Binary Tree Node public class Node { public int data; public Node left, right;

public Node(int v)
{
    data = v;
    left = right = null;
}

}

public class BinaryTree { // Function to print inorder traversal public static void printInorder(Node node) { if (node == null) return;

    // First recur on left subtree
    printInorder(node.left);

    // Now deal with the node
    Console.Write(node.data + " ");

    // Then recur on right subtree
    printInorder(node.right);
}

public static void Main()
{
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    printInorder(root);
}

}

JavaScript

// Structure of a Binary Tree Node class Node { constructor(v) { this.data = v; this.left = null; this.right = null; } }

// Function to print inorder traversal function printInorder(node) { if (node === null) { return; }

// First recur on left subtree
printInorder(node.left);

// Now deal with the node
console.log(node.data);

// Then recur on right subtree
printInorder(node.right);

}

const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);

printInorder(root);

**Time Complexity: O(n), n is the total number of nodes
**Auxiliary Space: O(h), h is the height of the tree.

In the worst case, **h can be the same as **N (when the tree is a skewed tree)
In the best case, **h can be the same as **log N (when the tree is a complete tree)

**Related Articles: