Morris traversal for Inorder (original) (raw)
Last Updated : 03 Feb, 2025
Given a **Binary Tree, the task is to print its **Inorder Traversal, without using **recursion or **stack.
**Examples:
**Input:
**Output: [4, 2, 5, 1, 3]
**Explanation: Inorder traversal ****(Left->Root->Right)** of the tree is 4, 2, 5, 1, 3.**Input:
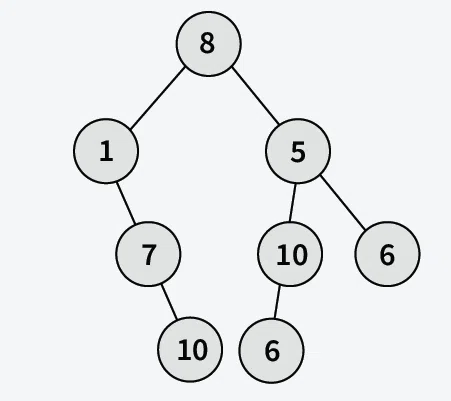
**Output: [1, 7, 10, 8, 6, 10, 5, 6]
**Explanation: Inorder traversal ****(Left->Root->Right)** of the tree is 1, 7, 10, 8, 6, 10, 5, 6.
**Approach:
Using **Morris Traversal, we can traverse the tree without using **stack and **recursion. The idea of Morris Traversal is based on Threaded Binary Tree. In this traversal, we first create links to **Inorder successor and print the data using these links, and finally revert the changes to restore original tree. Although the tree is modified through the traversal, it is reverted back to its original shape after the completion. Unlike Stack based traversal, no extra space is required for this traversal.
Step by step implementation:
- Initialize **current as root and repeat the following steps, as long as the current node is not **NULL.
- If the current node does not have a left child, print its data and move to the right, i.e., **current = current->right.
- Else, find **inorder predecessor of current (rightmost node in current left subtree or node whose **right child is equal to current).
- If we found that right child of inorder predecessor is equal to current then,
* update its the right child as NULL and print current’s data.
* Go to the right, i.e. **current = current->right. - Else
* Make current as the **right child of its **inorder predecessor; and
* Go to current's left child, i.e., **current = current->left.
- If we found that right child of inorder predecessor is equal to current then,
C++ `
//Driver Code Starts // C++ code to print Inorder Traversal // of Binary Tree using Morris Traversal #include #include using namespace std;
class Node { public: int data; Node* left; Node* right;
Node(int x) {
data = x;
left = right = nullptr;
}}; //Driver Code Ends
// Function for inorder traversal // using Morris Traversal vector inOrder(Node* root) { vector res; Node* curr = root;
while (curr != nullptr) {
if (curr->left == nullptr) {
// If no left child, visit this node
// and go right
res.push_back(curr->data);
curr = curr->right;
}
else {
// Find the inorder predecessor of curr
Node* prev = curr->left;
while (prev->right != nullptr &&
prev->right != curr) {
prev = prev->right;
}
// Make curr the right child of its
// inorder predecessor
if (prev->right == nullptr) {
prev->right = curr;
curr = curr->left;
}
else {
// Revert the changes made in
// the tree structure
prev->right = nullptr;
res.push_back(curr->data);
curr = curr->right;
}
}
}
return res;}
//Driver Code Starts
int main() {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
vector<int> res = inOrder(root);
for (int data : res) {
cout << data << " ";
}
return 0;}
//Driver Code Ends
C
//Driver Code Starts // C code to print Inorder Traversal // of Binary Tree using Morris Traversal #include <stdio.h> #include <stdlib.h>
struct Node { int data; struct Node* left; struct Node* right; }; //Driver Code Ends
// Function for inorder traversal using Morris Traversal void inOrder(struct Node* root, int res[], int* index) { struct Node* curr = root;
while (curr != NULL) {
if (curr->left == NULL) {
// If no left child, store this
// node's data and go right
res[(*index)++] = curr->data;
curr = curr->right;
}
else {
// Find the inorder predecessor of curr
struct Node* prev = curr->left;
while (prev->right != NULL
&& prev->right != curr) {
prev = prev->right;
}
// Make curr the right child of its
// inorder predecessor
if (prev->right == NULL) {
prev->right = curr;
curr = curr->left;
}
else {
// Revert the changes made in the tree
// structure
prev->right = NULL;
res[(*index)++] = curr->data;
curr = curr->right;
}
}
}}
//Driver Code Starts struct Node* createNode(int data) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = data; newNode->left = NULL; newNode->right = NULL; return newNode; }
int main() {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
struct Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
int res[100];
int index = 0;
inOrder(root, res, &index);
for (int i = 0; i < index; i++) {
printf("%d ", res[i]);
}
return 0;}
//Driver Code Ends
Java
//Driver Code Starts // Java code to print Inorder Traversal // of Binary Tree using Morris Traversal import java.util.*;
class Node { int data; Node left, right;
Node(int x) {
data = x;
left = right = null;
}}
class GfG { //Driver Code Ends
// Function for inorder traversal
// using Morris Traversal
static ArrayList<Integer> inOrder(Node root) {
ArrayList<Integer> res = new ArrayList<>();
Node curr = root;
while (curr != null) {
if (curr.left == null) {
// If no left child, visit this node
// and go right
res.add(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
Node prev = curr.left;
while (prev.right != null &&
prev.right != curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right == null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in
// the tree structure
prev.right = null;
res.add(curr.data);
curr = curr.right;
}
}
}
return res;
}//Driver Code Starts public static void main(String[] args) {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
ArrayList<Integer> res = inOrder(root);
for (int data : res) {
System.out.print(data + " ");
}
}}
//Driver Code Ends
Python
#Driver Code Starts
Python code to print Inorder Traversal
of Binary Tree using Morris Traversal
class Node: def init(self, data): self.data = data self.left = None self.right = None #Driver Code Ends
Function for inorder traversal using
Morris Traversal
def inOrder(root): res = [] curr = root
while curr is not None:
if curr.left is None:
# If no left child, visit this node
# and go right
res.append(curr.data)
curr = curr.right
else:
# Find the inorder predecessor of curr
prev = curr.left
while prev.right is not None \
and prev.right != curr:
prev = prev.right
# Make curr the right child of its
# inorder predecessor
if prev.right is None:
prev.right = curr
curr = curr.left
else:
# Revert the changes made in the
# tree structure
prev.right = None
res.append(curr.data)
curr = curr.right
return res#Driver Code Starts
if name == "main":
# Representation of input binary tree:
# 1
# / \
# 2 3
# / \
# 4 5
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
res = inOrder(root)
for data in res:
print(data, end=" ")#Driver Code Ends
C#
//Driver Code Starts // C# code to print Inorder Traversal // of Binary Tree using Morris Traversal using System; using System.Collections.Generic;
class Node { public int data; public Node left, right;
public Node(int x) {
data = x;
left = right = null;
}}
class GfG { //Driver Code Ends
// Function for inorder traversal using
// Morris Traversal
static List<int> inOrder(Node root) {
List<int> res = new List<int>();
Node curr = root;
while (curr != null) {
if (curr.left == null) {
// If no left child, visit this
// node and go right
res.Add(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
Node prev = curr.left;
while (prev.right != null
&& prev.right != curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right == null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in
// the tree structure
prev.right = null;
res.Add(curr.data);
curr = curr.right;
}
}
}
return res;
}//Driver Code Starts static void Main(string[] args) {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
List<int> res = inOrder(root);
foreach (int data in res) {
Console.Write(data + " ");
};
}}
//Driver Code Ends
JavaScript
//Driver Code Starts // Javascript code to print Inorder Traversal // of Binary Tree using Morris Traversal class Node { constructor(data) { this.data = data; this.left = null; this.right = null; } } //Driver Code Ends
// Function for inorder traversal using // Morris Traversal function inOrder(root) { let res = []; let curr = root;
while (curr !== null) {
if (curr.left === null) {
// If no left child, visit this
// node and go right
res.push(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
let prev = curr.left;
while (prev.right !== null
&& prev.right !== curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right === null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in the
// tree structure
prev.right = null;
res.push(curr.data);
curr = curr.right;
}
}
}
return res;}
//Driver Code Starts // Driver Code
// Representation of input binary tree:
// 1
// /
// 2 3
// / \
// 4 5
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
let res = inOrder(root);
console.log(res.join(' '));
//Driver Code Ends
`
Time Complexity: O(n), if we take a closer look, we can notice that every edge of the tree is traversed at most three times.
Auxiliary Space: O(1), as we are using only constant variables.