Insertion in Binary Search Tree (BST) (original) (raw)

Last Updated : 16 May, 2025

Given a **BST, the task is to insert a new node in this **BST.

**Example:

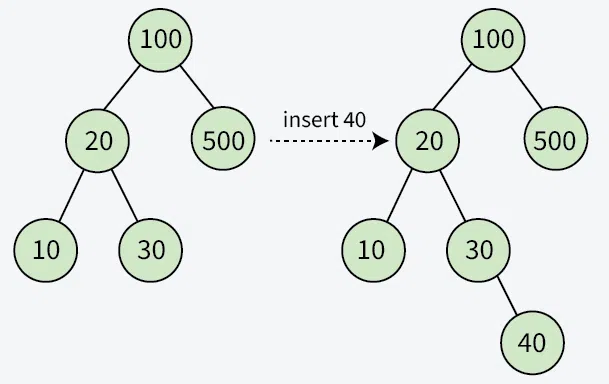
How to Insert a value in a Binary Search Tree:

A new key is always inserted at the leaf by maintaining the property of the binary search tree. We start searching for a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node. The below steps are followed while we try to insert a node into a binary search tree:

• Initilize the current node (say, **currNode or node) with root node
• Compare the **key with the current node.
• **Move left if the **key is less than or equal to the current node value.
• **Move right if the **key is greater than current node value.
• Repeat steps 2 and 3 until you reach a leaf node.
• Attach the new key as a left or right child based on the comparison with the leaf node's value.

Follow the below illustration for a better understanding:

**Insertion in Binary Search Tree using Recursion:

Below is the implementation of the insertion operation using recursion.

C++14 `

#include using namespace std;

struct Node { int key; Node* left; Node* right;
Node(int item) { key = item; left = NULL; right = NULL; } };

// A utility function to insert a new node with // the given key Node* insert(Node* node, int key) {

// If the tree is empty, return a new node
if (node == NULL) 
    return new Node(key);    

// If the key is already present in the tree,
// return the node
if (node->key == key) 
    return node;

// Otherwise, recur down the tree/ If the key
// to be inserted is greater than the node's key,
// insert it in the right subtree
if (node->key < key) 
    node->right = insert(node->right, key);

// If the key to be inserted is smaller than 
// the node's key,insert it in the left subtree
else 
    node->left = insert(node->left, key);

// Return the (unchanged) node pointer
return node;

}

// A utility function to do inorder tree traversal void inorder(Node* root) { if (root != NULL) { inorder(root->left); cout << root->key << " "; inorder(root->right); } }

// Driver program to test the above functions int main() { // Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

Node* root = new Node(50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);

// Print inorder traversal of the BST
inorder(root);

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

// Define the structure for a BST node struct Node { int key; struct Node* left; struct Node* right; };

// Function to create a new BST node struct Node* newNode(int item) { struct Node* temp = (struct Node*)malloc(sizeof(struct Node)); temp->key = item; temp->left = temp->right = NULL; return temp; }

// Function to insert a new node with the given key struct Node* insert(struct Node* node, int key) {

// If the tree is empty, return a new node
if (node == NULL)
    return newNode(key);

// If the key is already present in the tree,
// return the node
if (node->key == key)
    return node;

// Otherwise, recur down the tree. If the key 
// to be inserted is greater than the node's key,
// insert it in the right subtree
if (node->key < key)
    node->right = insert(node->right, key);

// If the key to be inserted is smaller than 
// the node's key,insert it in the left subtree
else
    node->left = insert(node->left, key);

// Return the (unchanged) node pointer
return node;

}

// Function to perform inorder tree traversal void inorder(struct Node* root) { if (root != NULL) { inorder(root->left); printf("%d ", root->key); inorder(root->right); } }

// Driver program to test the above functions int main() { // Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

struct Node* root = newNode(50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);

// Print inorder traversal of the BST
inorder(root);

return 0;

}

Java

class Node { int key; Node left, right;

public Node(int item)
{
    key = item;
    left = right = null;
}

}

class GfG {

// A utility function to insert a new node
// with the given key
static Node insert(Node root, int key)
{

    // If the tree is empty, return a new node
    if (root == null)
        return new Node(key);

    // If the key is already present in the tree,
    // return the node
    if (root.key == key)
        return root;

    // Otherwise, recur down the tree
    if (key < root.key)
        root.left = insert(root.left, key);
    else
        root.right = insert(root.right, key);

    // Return the (unchanged) node pointer
    return root;
}

// A utility function to do inorder tree traversal
static void inorder(Node root)
{
    if (root != null) {
        inorder(root.left);
        System.out.print(root.key + " ");
        inorder(root.right);
    }
}

// Driver method
public static void main(String[] args)
{
    Node root = null;

    // Creating the following BST
    //      50
    //     /  \
    //    30   70
    //   / \   / \
    //  20 40 60 80

    root = insert(root, 50);
    root = insert(root, 30);
    root = insert(root, 20);
    root = insert(root, 40);
    root = insert(root, 70);
    root = insert(root, 60);
    root = insert(root, 80);

    // Print inorder traversal of the BST
    inorder(root);
}

}

Python

Python program to demonstrate

insert operation in binary search tree

class Node: def init(self, key): self.left = None self.right = None self.val = key

A utility function to insert

a new node with the given key

def insert(root, key): if root is None: return Node(key) if root.val == key: return root if root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root

A utility function to do inorder tree traversal

def inorder(root): if root: inorder(root.left) print(root.val, end=" ") inorder(root.right)

Creating the following BST

50

/ \

30 70

/ \ / \

20 40 60 80

r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80)

Print inorder traversal of the BST

inorder(r)

C#

using System;

class Node { public int key; public Node left, right;

public Node(int item) {
    key = item;
    left = right = null;
}

}

class GfG {

// A function to insert a new node with the given key
public static Node Insert(Node node, int key) {
    if (node == null)
        return new Node(key);
  
    // Duplicates not allowed
    if (key == node.key)
        return node;
  
    if (key < node.key)
        node.left = Insert(node.left, key);
    else if (key > node.key)
        node.right = Insert(node.right, key);

    return node;
}

// A utility function to do inorder tree traversal
public static void Inorder(Node root) {
    if (root != null) {
        Inorder(root.left);
        Console.Write(root.key + " ");
        Inorder(root.right);
    }
}

// Driver method
public static void Main() {
    // Creating the following BST
    //      50
    //     /  \
    //    30   70
    //   / \   / \
    //  20 40 60 80

    Node root = new Node(50);
    root = Insert(root, 30);
    root = Insert(root, 20);
    root = Insert(root, 40);
    root = Insert(root, 70);
    root = Insert(root, 60);
    root = Insert(root, 80);

    // Print inorder traversal of the BST
    Inorder(root);
}

}

JavaScript

class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } }

// A utility function to insert a new // node with the given key function insert(root, key) {

if (root === null)
    return new Node(key);
    
// Duplicates not allowed    
if (root.key === key)
    return root;
    
if (key < root.key)
    root.left = insert(root.left, key);
else if (key > root.key)
    root.right = insert(root.right, key);

return root;

}

// A utility function to do inorder // tree traversal function inorder(root) { if (root !== null) { inorder(root.left); console.log(root.key + " "); inorder(root.right); } }

// Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

let root = new Node(50); root = insert(root, 30); root = insert(root, 20); root = insert(root, 40); root = insert(root, 70); root = insert(root, 60); root = insert(root, 80);

// Print inorder traversal of the BST inorder(root);

`

Output

20 30 40 50 60 70 80

**Time Complexity:

• The worst-case time complexity of insert operations is O(h) where **h is the height of the Binary Search Tree.
• In the worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become **n and the time complexity of insertion operation may become O(n).

**Auxiliary Space: The auxiliaryspace complexity of insertion into a binary search tree is O(h), due to recursive stack.

**Insertion in Binary Search Tree using Iterative approach:

Instead of using recursion, we can also implement the insertion operation iteratively using a **while loop. Below is the implementation using a while loop.

C++ `

#include using namespace std;

struct Node { int key; Node* left; Node* right; Node(int item) { key = item; left = NULL; right = NULL; } };

Node* insert(Node* root, int x) {

Node* temp = new Node(x);

// If tree is empty
if (root == NULL)
    return temp;

// Find the node who is going
// to have the new node temp as
// it child. The parent node is
// mainly going to be a leaf node
Node *parent = NULL, *curr = root;
while (curr != NULL) {
    parent = curr;
    if (curr->key > x)
        curr = curr->left;
    else if (curr->key < x)
        curr = curr->right;
    else
        return root;
}

// If x is smaller, make it
// left child, else right child
if (parent->key > x)
    parent->left = temp;
else
    parent->right = temp;
return root;

}

// A utility function to do inorder // tree traversal void inorder(Node* root) { if (root != NULL) { inorder(root->left); cout << root->key << " "; inorder(root->right); } }

// Driver program int main() { // Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

Node* root = new Node(50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);

// Print inorder traversal of the BST
inorder(root);

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

// Define the structure for a BST node struct Node { int key; struct Node* left; struct Node* right; };

// Function to create a new BST node struct Node* newNode(int item) { struct Node* temp = (struct Node*)malloc(sizeof(struct Node)); temp->key = item; temp->left = temp->right = NULL; return temp; }

struct Node* insert(struct Node* root, int x) {

struct Node* temp = newNode(x);

// If tree is empty
if (root == NULL)
    return temp;

// Find the node who is going
// to have the new node temp as
// it child. The parent node is
// mainly going to be a leaf node
struct Node *parent = NULL, *curr = root;
while (curr != NULL) {
    parent = curr;
    if (curr->key > x)
        curr = curr->left;
    else if (curr->key < x)
        curr = curr->right;
    else
        return root;
}

// If x is smaller, make it
// left child, else right child
if (parent->key > x)
    parent->left = temp;
else
    parent->right = temp;
return root;

}

// Function to perform inorder tree traversal void inorder(struct Node* root) { if (root != NULL) { inorder(root->left); printf("%d ", root->key); inorder(root->right); } }

// Driver program to test the above functions int main() { // Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

struct Node* root = newNode(50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);

// Print inorder traversal of the BST
inorder(root);

return 0;

}

Java

class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } }

class GfG {

// Function to insert a new node with
// the given key
static Node insert(Node root, int x) {
    Node temp = new Node(x);

    // If tree is empty
    if (root == null) {
        return temp;
    }

    // Find the node who is going to have 
    // the new node temp as its child
    Node parent = null;
    Node curr = root;
    while (curr != null) {
        parent = curr;
        if (curr.key > x) {
            curr = curr.left;
        } else if (curr.key < x) {
            curr = curr.right;
        } else {
            return root; // Key already exists
        }
    }

    // If x is smaller, make it left 
    // child, else right child
    if (parent.key > x) {
        parent.left = temp;
    } else {
        parent.right = temp;
    }
    return root;
}

// A utility function to do inorder tree traversal
static void inorder(Node root)
{
    if (root != null) {
        inorder(root.left);
        System.out.print(root.key + " ");
        inorder(root.right);
    }
}

// Driver method
public static void main(String[] args)
{
    Node root = null;

    // Creating the following BST
    //      50
    //     /  \
    //    30   70
    //   / \   / \
    //  20 40 60 80

    root = insert(root, 50);
    root = insert(root, 30);
    root = insert(root, 20);
    root = insert(root, 40);
    root = insert(root, 70);
    root = insert(root, 60);
    root = insert(root, 80);

    // Print inorder traversal of the BST
    inorder(root);
}

}

Python

Python program to demonstrate

insert operation in binary search tree

class Node: def init(self, key): self.left = None self.right = None self.key = key

def insert(root, key): temp = Node(key)

# If tree is empty
if root is None:
    return temp

# Find the node who is going to 
# have the new node temp as its child
parent = None
curr = root
while curr is not None:
    parent = curr
    if curr.key > key:
        curr = curr.left
    elif curr.key < key:
        curr = curr.right
    else:
        return root  # Key already exists

# If key is smaller, make it left 
# child, else right child
if parent.key > key:
    parent.left = temp
else:
    parent.right = temp

return root

A utility function to do inorder tree traversal

def inorder(root): if root: inorder(root.left) print(root.key, end=" ") inorder(root.right)

Creating the following BST

50

/ \

30 70

/ \ / \

20 40 60 80

r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80)

Print inorder traversal of the BST

inorder(r)

C#

using System;

class Node { public int key; public Node left, right;

public Node(int item) {
    key = item;
    left = right = null;
}

}

class GfG {

// Function to insert a new node with the given key
public static Node Insert(Node root, int x)
{
    Node temp = new Node(x);

    // If tree is empty
    if (root == null)
        return temp;

    // Find the node who is going to 
    // have the new node temp as its child
    Node parent = null;
    Node curr = root;
    while (curr != null)
    {
        parent = curr;
        if (curr.key > x)
            curr = curr.left;
        else if (curr.key < x)
            curr = curr.right;
        else
            return root; // Key already exists
    }

    // If x is smaller, make it left 
    // child, else right child
    if (parent.key > x)
        parent.left = temp;
    else
        parent.right = temp;

    return root;
}

// A utility function to do inorder tree traversal
public static void Inorder(Node root) {
    if (root != null) {
        Inorder(root.left);
        Console.Write(root.key + " ");
        Inorder(root.right);
    }
}

// Driver method
public static void Main() {
    // Creating the following BST
    //      50
    //     /  \
    //    30   70
    //   / \   / \
    //  20 40 60 80

    Node root = new Node(50);
    root = Insert(root, 30);
    root = Insert(root, 20);
    root = Insert(root, 40);
    root = Insert(root, 70);
    root = Insert(root, 60);
    root = Insert(root, 80);

    // Print inorder traversal of the BST
    Inorder(root);
}

}

JavaScript

class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } }

// Function to insert a new node with the given key function insert(root, x) { const temp = new Node(x);

// If tree is empty
if (root === null)
    return temp;

// Find the node who is going to have
// the new node temp as its child
let parent = null;
let curr = root;
while (curr !== null) {
    parent = curr;
    if (curr.key > x)
        curr = curr.left;
    else if (curr.key < x)
        curr = curr.right;
    else
        return root; // Key already exists
}

// If x is smaller, make it left
// child, else right child
if (parent.key > x)
    parent.left = temp;
else
    parent.right = temp;

return root;

}

// A utility function to do inorder tree traversal function inorder(root) { if (root !== null) { inorder(root.left); console.log(root.key + " "); inorder(root.right); } }

// Creating the following BST // 50 // /
// 30 70 // / \ /
// 20 40 60 80

let root = new Node(50); root = insert(root, 30); root = insert(root, 20); root = insert(root, 40); root = insert(root, 70); root = insert(root, 60); root = insert(root, 80);

// Print inorder traversal of the BST inorder(root);

`

Output

20 30 40 50 60 70 80

The **time complexity of **inorder traversal is **O(h), where h is the height of the tree.
The **Auxiliary space is **O(1)

**Related Links:

• Binary Search Tree Search Operation
• Binary Search Tree Delete Operation