Introduction to Binary Tree (original) (raw)

**Binary Tree is a **non-linear and hierarchical data structure where each node has at most two children referred to as the **left child and the right child. The topmost node in a binary tree is called the **root, and the bottom-most nodes are called **leaves.

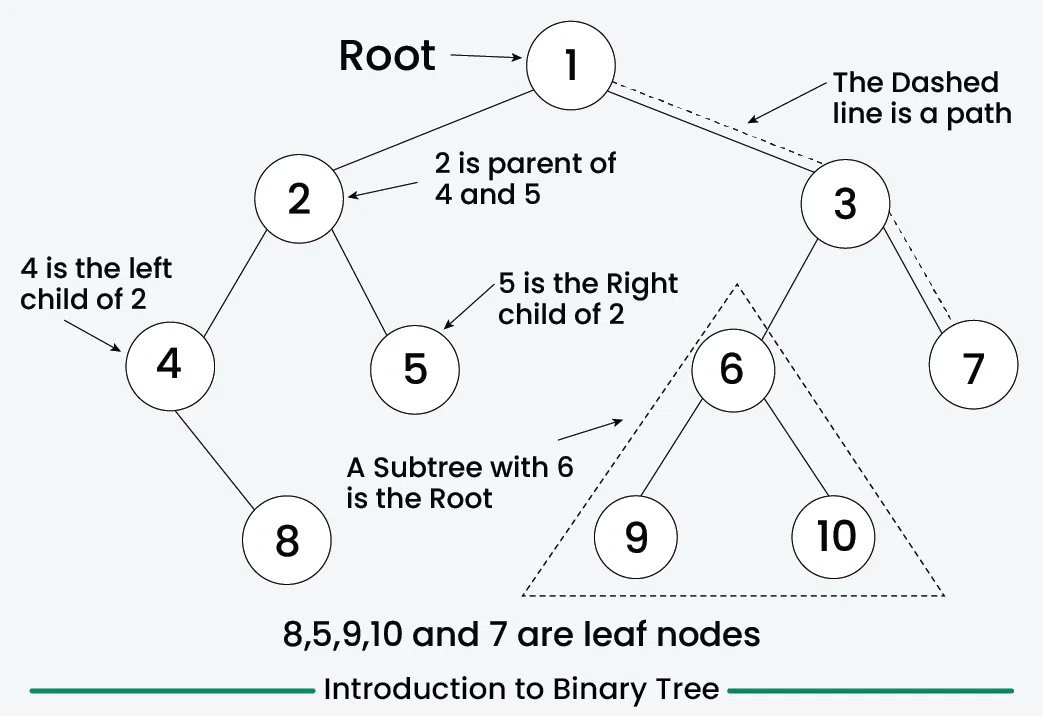
Introduction-to-Binary-Tree

Introduction to Binary Tree

**Representation of Binary Tree

Each node in a Binary Tree has three parts:

Data
Pointer to the left child
Pointer to the right child

Binary-Tree-Representation

Binary Tree Representation

Create/Declare a Node of a Binary Tree

Syntax to declare a Node of Binary Tree in different languages:

C++ `

// Use any below method to implement Nodes of binary tree

// 1: Using struct struct Node { int data; Node* left, * right;

Node(int key) {
    data = key;
    left = nullptr;
    right = nullptr;
}

};

// 2: Using class class Node { public: int data; Node* left, * right;

Node(int key) {
    data = key;
    left = nullptr;
    right = nullptr;
}

};

C

// Structure of each node of the tree. struct Node { int data; struct Node* left; struct Node* right; };

// Note : Unlike other languages, C does not support // Object Oriented Programming. So we need to write // a separat method for create and instance of tree node struct Node* newNode(int item) { struct Node* temp = (struct Node*)malloc(sizeof(struct Node)); temp->key = item; temp->left = temp->right = NULL; return temp; }

Java

// Class containing left and right child // of current node and key value class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } }

Python

A Python class that represents

an individual node in a Binary Tree

class Node: def init(self, key): self.left = None self.right = None self.val = key

C#

// Class containing left and right child // of current node and key value class Node { int key; Node left, right;

public Node(int item)
{
    key = item;
    left = right = null;
}

}

JavaScript

/* Class containing left and right child of current node and data*/

class Node { constructor(item) { this.data = item; this.left = this.right = null; } }

Example for Creating a Binary Tree

Here’s an example of creating a Binary Tree with four nodes (2, 3, 4, 5)

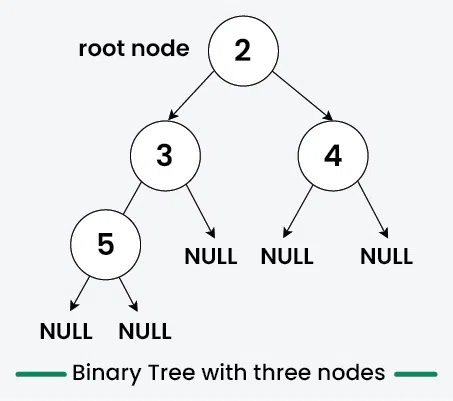
Binary-Tree-with-three-nodes

Creating a Binary Tree having three nodes

C++ `

#include using namespace std;

struct Node{ int data; Node *left, *right; Node(int d){ data = d; left = nullptr; right = nullptr; } };

int main(){ // Initilize and allocate memory for tree nodes Node* firstNode = new Node(2); Node* secondNode = new Node(3); Node* thirdNode = new Node(4); Node* fourthNode = new Node(5);

// Connect binary tree nodes
firstNode->left = secondNode;
firstNode->right = thirdNode;
secondNode->left = fourthNode;
return 0;

}

C

#include <stdio.h> #include <stdlib.h>

struct Node { int data; struct Node *left; struct Node *right; };

struct Node* createNode(int d) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = d; newNode->left = NULL; newNode->right = NULL; return newNode; }

int main() { // Initialize and allocate memory for tree nodes struct Node* firstNode = createNode(2); struct Node* secondNode = createNode(3); struct Node* thirdNode = createNode(4); struct Node* fourthNode = createNode(5);

// Connect binary tree nodes
firstNode->left = secondNode;
firstNode->right = thirdNode;
secondNode->left = fourthNode;

return 0;

}

Java

class Node { int data; Node left, right; Node(int d) { data = d; left = null; right = null; } }

class GfG { public static void main(String[] args) { // Initialize and allocate memory for tree nodes Node firstNode = new Node(2); Node secondNode = new Node(3); Node thirdNode = new Node(4); Node fourthNode = new Node(5);

    // Connect binary tree nodes
    firstNode.left = secondNode;
    firstNode.right = thirdNode;
    secondNode.left = fourthNode;

}

}

Python

class Node: def init(self, d): self.data = d self.left = None self.right = None

Initialize and allocate memory for tree nodes

firstNode = Node(2) secondNode = Node(3) thirdNode = Node(4) fourthNode = Node(5)

Connect binary tree nodes

firstNode.left = secondNode firstNode.right = thirdNode secondNode.left = fourthNode

C#

using System;

class Node { public int data; public Node left, right;

public Node(int d) {
    this.data = d;
    left = null;
    right = null;
}

}

class GfG { static void Main() { // Initialize and allocate memory for tree nodes Node firstNode = new Node(2); Node secondNode = new Node(3); Node thirdNode = new Node(4); Node fourthNode = new Node(5);

    // Connect binary tree nodes
    firstNode.left = secondNode;
    firstNode.right = thirdNode;
    secondNode.left = fourthNode;
}

}

JavaScript

class Node { constructor(d) { this.data = d; this.left = null; this.right = null; } }

// Initialize and allocate memory for tree nodes let firstNode = new Node(2); let secondNode = new Node(3); let thirdNode = new Node(4); let fourthNode = new Node(5);

// Connect binary tree nodes firstNode.left = secondNode; firstNode.right = thirdNode; secondNode.left = fourthNode;

In the above code, we have created four tree nodes **firstNode, **secondNode, **thirdNode and **fourthNode having values **2, **3, **4 and 5 respectively.

After creating three nodes, we have connected these node to form the tree structure like mentioned in above image.
Connect the **secondNode to the left of **firstNode by **firstNode->left = secondNode
Connect the **thirdNode to the right of **firstNode by **firstNode->right = thirdNode
Connect the **fourthNode to the left of **secondNode by **secondNode->left = fourthNode

Terminologies in Binary Tree

**Nodes: The fundamental part of a binary tree, where each node contains **data and **link to two child nodes.
**Root: The topmost node in a tree is known as the root node. It has no parent and serves as the starting point for all nodes in the tree.
**Parent Node: A node that has one or more child nodes. In a binary tree, each node can have at most two children.
**Child Node: A node that is a descendant of another node (its parent).
**Leaf Node: A node that does not have any children or both children are null.
**Internal Node: A node that has at least one child. This includes all nodes except the **leaf nodes.
**Depth of a Node: The number of edges from a specific node to the root node. The depth of the **root node is zero.
**Height of a Binary Tree: The number of nodes from the deepest leaf node to the root node.

The diagram below shows all these terms in a binary tree.

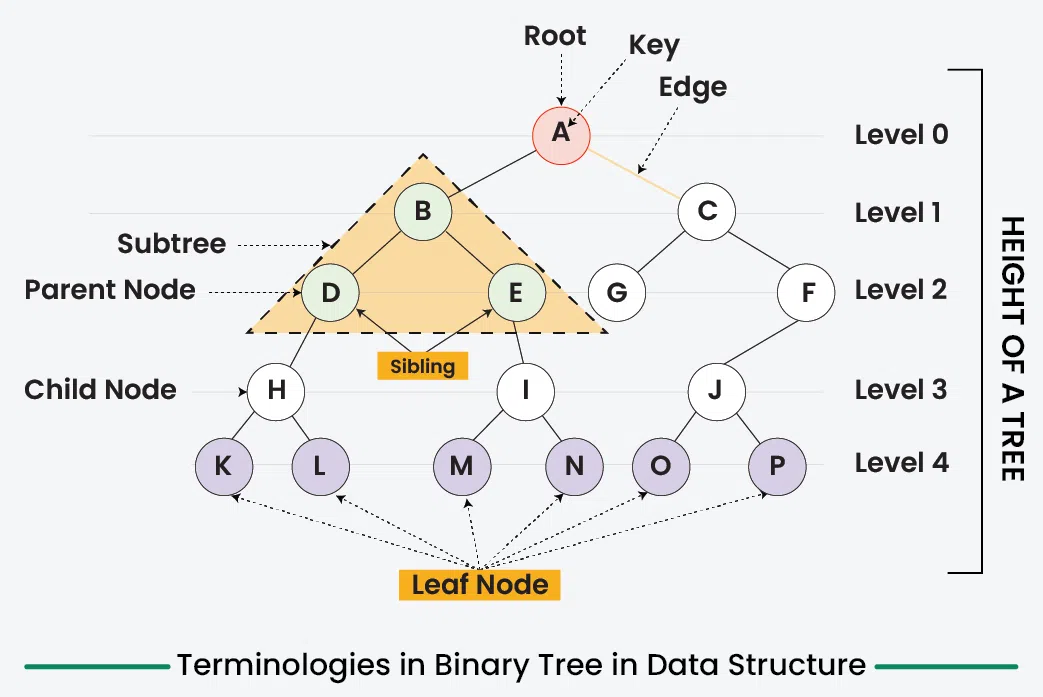
Terminologies-in-Binary-Tree-in-Data-Structure_1

Terminologies in Binary Tree in Data Structure

Properties of Binary Tree

The maximum number of nodes at level **L of a binary tree is 2 L
The maximum number of nodes in a binary tree of height **H is **2 H – 1
Total number of leaf nodes in a binary tree = total number of nodes with 2 children + 1
In a Binary Tree with **N nodes, the minimum possible height or the minimum number of levels is **Log 2 (N+1)
A Binary Tree with L leaves has at least | Log2L |+ 1 levels

Please refer Properties of Binary Tree for more details.

Types of Binary Tree

Binary Tree can be classified into multiples types based on multiple factors:

**On the basis of Number of Children
**On the basis of Completion of Levels
**On the basis of Node Values:

**Operations On Binary Tree

Following is a list of common operations that can be performed on a binary tree:

1. Traversal in Binary Tree

Traversal in Binary Tree involves visiting all the nodes of the binary tree. Tree Traversal algorithms can be classified broadly into two categories, **DFS and **BFS:

**Depth-First Search (DFS) algorithms: DFS explores as far down a branch as possible before backtracking. It is implemented using recursion. The main traversal methods in DFS for binary trees are:

**Preorder Traversal (current-left-right): Visits the **node first, then **left subtree, then **right subtree.
**Inorder Traversal (left-current-right):Visits **left subtree, then the **node, then the **right subtree.
**Postorder Traversal (left-right-current): Visits **left subtree, then **right subtree, then the **node.

Breadth-First Search (BFS) algorithms: BFS explores all nodes at the present depth before moving on to nodes at the next depth level. It is typically implemented using a queue.BFS in a binary tree is commonly referred to as**Level Order Traversal.

Below is the implementation of traversals algorithm in binary tree:

C++ `

#include <bits/stdc++.h> using namespace std;

struct Node { int data; Node* left, * right;

Node(int d) {
    data = d;
    left = nullptr;
    right = nullptr;
}

};

// In-order DFS: Left, Root, Right void inOrderDFS(Node* node) { if (node == nullptr) return;

inOrderDFS(node->left);
cout << node->data << " ";
inOrderDFS(node->right);

}

// Pre-order DFS: Root, Left, Right void preOrderDFS(Node* node) { if (node == nullptr) return;

cout << node->data << " ";
preOrderDFS(node->left);
preOrderDFS(node->right);

}

// Post-order DFS: Left, Right, Root void postOrderDFS(Node* node) { if (node == nullptr) return;

postOrderDFS(node->left);
postOrderDFS(node->right);
cout << node->data << " ";

}

void BFS(Node* root) {

if (root == nullptr) return;
queue<Node*> q;
q.push(root);

while (!q.empty()) {
    Node* node = q.front();
    q.pop(); 
    cout << node->data << " ";
    if (node->left != nullptr) q.push(node->left);
    if (node->right != nullptr) q.push(node->right);
    
}

}

int main() { Node* root = new Node(2); root->left = new Node(3); root->right = new Node(4); root->left->left = new Node(5);

cout << "In-order DFS: ";
inOrderDFS(root);

cout << "\nPre-order DFS: ";
preOrderDFS(root);

cout << "\nPost-order DFS: ";
postOrderDFS(root);

cout << "\nLevel order: ";
BFS(root);

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

struct Node{ int data; struct Node *left; struct Node *right; };

// In-order DFS: Left, Root, Right void inOrderDFS(struct Node *node){ if (node == NULL) return; inOrderDFS(node->left); printf("%d ", node->data); inOrderDFS(node->right); }

// Pre-order DFS: Root, Left, Right void preOrderDFS(struct Node *node){ if (node == NULL) return; printf("%d ", node->data); preOrderDFS(node->left); preOrderDFS(node->right); }

// Post-order DFS: Left, Right, Root void postOrderDFS(struct Node *node){ if (node == NULL) return; postOrderDFS(node->left); postOrderDFS(node->right); printf("%d ", node->data); }

// BFS: Level order traversal void BFS(struct Node *root){ if (root == NULL) return; struct Node *queue[100]; int front = 0, rear = 0; queue[rear++] = root;

while (front < rear) {
    struct Node *node = queue[front++];
    printf("%d ", node->data);
    if (node->left)
        queue[rear++] = node->left;
    if (node->right)
        queue[rear++] = node->right;
}

}

struct Node *createNode(int d){ struct Node *newNode = (struct Node *)malloc(sizeof(struct Node)); newNode->data = d; newNode->left = NULL; newNode->right = NULL; return newNode; }

int main(){ // Creating the tree struct Node *root = (struct Node *)malloc(sizeof(struct Node)); root->data = 2; root->left = (struct Node *)malloc(sizeof(struct Node)); root->left->data = 3; root->right = (struct Node *)malloc(sizeof(struct Node)); root->right->data = 4; root->left->left = (struct Node *)malloc(sizeof(struct Node)); root->left->left->data = 5;

printf("In-order DFS: ");
inOrderDFS(root);
printf("\nPre-order DFS: ");
preOrderDFS(root);
printf("\nPost-order DFS: ");
postOrderDFS(root);
printf("\nLevel order: ");
BFS(root);

return 0;

}

Java

import java.util.LinkedList; import java.util.Queue;

class Node { int data; Node left, right;

Node(int d) {
    data = d;
    left = right = null;
}

}

// BinaryTree class class GfG { // In-order DFS: Left, Root, Right static void inOrderDFS(Node node) { if (node == null) return; inOrderDFS(node.left); System.out.print(node.data + " "); inOrderDFS(node.right); }

// Pre-order DFS: Root, Left, Right
static void preOrderDFS(Node node) {
    if (node == null) return;
    System.out.print(node.data + " ");
    preOrderDFS(node.left);
    preOrderDFS(node.right);
}

// Post-order DFS: Left, Right, Root
static void postOrderDFS(Node node) {
    if (node == null) return;
    postOrderDFS(node.left);
    postOrderDFS(node.right);
    System.out.print(node.data + " ");
}

// BFS: Level order traversal
static void BFS(Node root) {
    if (root == null) return;
    Queue<Node> queue = new LinkedList<>();
    queue.add(root);

    while (!queue.isEmpty()) {
        Node node = queue.poll();
        System.out.print(node.data + " ");
        if (node.left != null) queue.add(node.left);
        if (node.right != null) queue.add(node.right);
    }
}

public static void main(String[] args) {
    // Creating the tree
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);

   
    System.out.print("In-order DFS: ");
    inOrderDFS(root);
    System.out.print("\nPre-order DFS: ");
    preOrderDFS(root);
    System.out.print("\nPost-order DFS: ");
    postOrderDFS(root);
    System.out.print("\nLevel order: ");
    BFS(root);
}

}

Python

class Node: def init(self, data): self.data = data self.left = None self.right = None

In-order DFS: Left, Root, Right

def in_order_dfs(node): if node is None: return in_order_dfs(node.left) print(node.data, end=' ') in_order_dfs(node.right)

Pre-order DFS: Root, Left, Right

def pre_order_dfs(node): if node is None: return print(node.data, end=' ') pre_order_dfs(node.left) pre_order_dfs(node.right)

Post-order DFS: Left, Right, Root

def post_order_dfs(node): if node is None: return post_order_dfs(node.left) post_order_dfs(node.right) print(node.data, end=' ')

BFS: Level order traversal

def bfs(root): if root is None: return queue = [root] while queue: node = queue.pop(0) print(node.data, end=' ') if node.left: queue.append(node.left) if node.right: queue.append(node.right)

if name == "main": # Creating the tree root = Node(2) root.left = Node(3) root.right = Node(4) root.left.left = Node(5)

print("In-order DFS: ", end='')
in_order_dfs(root)
print("\nPre-order DFS: ", end='')
pre_order_dfs(root)
print("\nPost-order DFS: ", end='')
post_order_dfs(root)
print("\nLevel order: ", end='')
bfs(root)

C#

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int d) {
    data = d;
    left = right = null;
}

}

class GfG { // In-order DFS: Left, Root, Right static void InOrderDFS(Node node) { if (node == null) return; InOrderDFS(node.left); Console.Write(node.data + " "); InOrderDFS(node.right); }

// Pre-order DFS: Root, Left, Right
static void PreOrderDFS(Node node) {
    if (node == null) return;
    Console.Write(node.data + " ");
    PreOrderDFS(node.left);
    PreOrderDFS(node.right);
}

// Post-order DFS: Left, Right, Root
static void PostOrderDFS(Node node) {
    if (node == null) return;
    PostOrderDFS(node.left);
    PostOrderDFS(node.right);
    Console.Write(node.data + " ");
}

// BFS: Level order traversal
static public void BFS(Node root) {
    if (root == null) return;
    Queue<Node> queue = new Queue<Node>();
    queue.Enqueue(root);

    while (queue.Count > 0) {
        Node node = queue.Dequeue();
        Console.Write(node.data + " ");
        if (node.left != null) queue.Enqueue(node.left);
        if (node.right != null) queue.Enqueue(node.right);
    }
}

public static void Main(string[] args) {
    // Creating the tree
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);

    Console.Write("In-order DFS: ");
    InOrderDFS(root);
    Console.Write("\nPre-order DFS: ");
    PreOrderDFS(root);
    Console.Write("\nPost-order DFS: ");
    PostOrderDFS(root);
    Console.Write("\nLevel order: ");
    BFS(root);
}

}

JavaScript

// Node structure class Node { constructor(data) { this.data = data; this.left = null; this.right = null; } }

// In-order DFS: Left, Root, Right function inOrderDFS(node) { if (node === null) return; inOrderDFS(node.left); console.log(node.data + " "); inOrderDFS(node.right); }

// Pre-order DFS: Root, Left, Right function preOrderDFS(node) { if (node === null) return; process.stdout.write(node.data + " "); preOrderDFS(node.left); preOrderDFS(node.right); }

// Post-order DFS: Left, Right, Root function postOrderDFS(node) { if (node === null) return; postOrderDFS(node.left); postOrderDFS(node.right); process.stdout.write(node.data + " "); }

// BFS: Level order traversal function bfs(root) { if (root === null) return; let queue = [root]; while (queue.length > 0) { let node = queue.shift(); process.stdout.write(node.data + " "); if (node.left) queue.push(node.left); if (node.right) queue.push(node.right); } }

// Creating the tree let root = new Node(2); root.left = new Node(3); root.right = new Node(4); root.left.left = new Node(5);

console.log("In-order DFS: "); inOrderDFS(root); console.log("\nPre-order DFS: "); preOrderDFS(root); console.log("\nPost-order DFS: "); postOrderDFS(root); console.log("\nLevel order: "); bfs(root);

Output

In-order DFS: 5 3 2 4 Pre-order DFS: 2 3 5 4 Post-order DFS: 5 3 4 2 Level order: 2 3 4 5

2. Insertion in Binary Tree

Inserting elements means add a new node into the binary tree. As we know that there is no such ordering of elements in the binary tree, So we do not have to worry about the ordering of node in the binary tree. We would first creates a **root node in case of empty tree. Then subsequent insertions involve iteratively searching for an empty place at each level of the tree. When an empty **left or **right child is found then **new node is inserted there. By convention, insertion always starts with the **left child node.

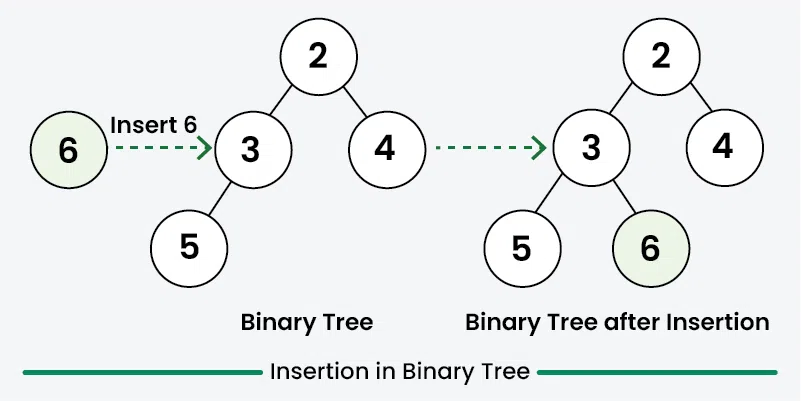
Insertion-in-Binary-Tree

Insertion in Binary Tree

C++ `

#include <bits/stdc++.h> using namespace std;

struct Node { int data; Node* left, * right; Node(int d) { data = d; left = right = nullptr; } };

// Function to insert a new node in the binary tree Node* insert(Node* root, int key) { // If the tree is empty, create the root node if (root == nullptr) { root = new Node(key); return root; } // Create a queue for level order traversal queue<Node*> q; q.push(root);

// Do level order traversal until we find an empty place
while (!q.empty()) {
    Node* temp = q.front();
    q.pop();

    // If left child is empty, insert the new node here
    if (temp->left == nullptr) {
        temp->left = new Node(key);
        break;
    } else {
        q.push(temp->left);
    }
    // If right child is empty, insert the new node here
    if (temp->right == nullptr) {
        temp->right = new Node(key);
        break;
    } else {
        q.push(temp->right);
    }
}
return root;

}

void inorder(Node* root) { if (root == nullptr) return; inorder(root->left); cout << root->data << " "; inorder(root->right); }

int main() { Node* root = new Node(2); root->left = new Node(3); root->right = new Node(4) ; root->left->left = new Node(5);

cout << "Inorder traversal before insertion: ";
inorder(root);
cout << endl;

int key = 6;
root = insert(root, key);

cout << "Inorder traversal after insertion: ";
inorder(root);
cout << endl;

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

struct Node { int data; struct Node* left; struct Node* right; };

struct Node* createNode(int d);

// Function to insert a new node in the binary tree struct Node* insert(struct Node* root, int key) { if (root == NULL) return createNode(key);

// Create a queue for level order traversal
struct Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;

while (front < rear) {
    struct Node* temp = queue[front++];

    // If left child is empty, insert the new node here
    if (temp->left == NULL) {
        temp->left = createNode(key);
        break;
    } else {
        queue[rear++] = temp->left;
    }

    // If right child is empty, insert the new node here
    if (temp->right == NULL) {
        temp->right = createNode(key);
        break;
    } else {
        queue[rear++] = temp->right;
    }
}
return root;

}

void inorder(struct Node* root) { if (root == NULL) return; inorder(root->left); printf("%d ", root->data); inorder(root->right); }

struct Node* createNode(int d) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = d; newNode->left = NULL; newNode->right = NULL; return newNode; }

int main() { struct Node* root = createNode(2); root->left = createNode(3); root->right = createNode(4); root->left->left = createNode(5);

printf("Inorder traversal before insertion: ");
inorder(root);
printf("\n");

int key = 6;
root = insert(root, key);

printf("Inorder traversal after insertion: ");
inorder(root);
printf("\n");

return 0;

}

Java

import java.util.LinkedList; import java.util.Queue;

class Node { int data; Node left, right;

Node(int d) {
    data = d;
    left = right = null;
}

}

class GfG { // Function to insert a new node in the binary tree static Node insert(Node root, int key) { if (root == null) return new Node(key);

    // Create a queue for level order traversal
    Queue<Node> q = new LinkedList<>();
    q.add(root);

    while (!q.isEmpty()) {
        Node temp = q.poll();

        // If left child is empty, insert the new node here
        if (temp.left == null) {
            temp.left = new Node(key);
            break;
        } else {
            q.add(temp.left);
        }

        // If right child is empty, insert the new node here
        if (temp.right == null) {
            temp.right = new Node(key);
            break;
        } else {
            q.add(temp.right);
        }
    }
    return root;
}

// In-order traversal
static void inorder(Node root) {
    if (root == null) return;
    inorder(root.left);
    System.out.print(root.data + " ");
    inorder(root.right);
}

public static void main(String[] args) {
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);

    System.out.print("Inorder traversal before insertion: ");
    inorder(root);
    System.out.println();

    int key = 6;
    root = insert(root, key);

    System.out.print("Inorder traversal after insertion: ");
    inorder(root);
    System.out.println();
}

}

Python

from collections import deque

class Node: def init(self, d): self.data = d self.left = None self.right = None

Function to insert a new node in the binary tree

def insert(root, key): if root is None: return Node(key)

# Create a queue for level order traversal
queue = deque([root])

while queue:
    temp = queue.popleft()

    # If left child is empty, insert the new node here
    if temp.left is None:
        temp.left = Node(key)
        break
    else:
        queue.append(temp.left)

    # If right child is empty, insert the new node here
    if temp.right is None:
        temp.right = Node(key)
        break
    else:
        queue.append(temp.right)

return root

In-order traversal

def inorder(root): if root is None: return inorder(root.left) print(root.data, end=" ") inorder(root.right)

if name == "main": root = Node(2) root.left = Node(3) root.right = Node(4) root.left.left = Node(5)

print("Inorder traversal before insertion: ", end="")
inorder(root)
print()

key = 6
root = insert(root, key)

print("Inorder traversal after insertion: ", end="")
inorder(root)
print()

C#

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int d) {
    data = d;
    left = right = null;
}

}

class GfG { // Function to insert a new node in the binary tree static Node Insert(Node root, int key) { if (root == null) { return new Node(key); }

    // Create a queue for level order traversal
    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);

    while (q.Count > 0) {
        Node temp = q.Dequeue();

        // If left child is empty, insert the new node here
        if (temp.left == null) {
            temp.left = new Node(key);
            break;
        } else {
            q.Enqueue(temp.left);
        }

        // If right child is empty, insert the new node here
        if (temp.right == null) {
            temp.right = new Node(key);
            break;
        } else {
            q.Enqueue(temp.right);
        }
    }
    return root;
}

// In-order traversal
static void Inorder(Node root) {
    if (root == null) return;
    Inorder(root.left);
    Console.Write(root.data + " ");
    Inorder(root.right);
}

static void Main() {
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);

    Console.Write("Inorder traversal before insertion: ");
    Inorder(root);
    Console.WriteLine();

    int key = 6;
    root = Insert(root, key);

    Console.Write("Inorder traversal after insertion: ");
    Inorder(root);
    Console.WriteLine();
}

}

JavaScript

class Node { constructor(d) { this.data = d; this.left = null; this.right = null; } }

// Function to insert a new node in the binary tree function insert(root, key) { if (root === null) { return new Node(key); }

// Create a queue for level order traversal
let queue = [root];

while (queue.length > 0) {
    let temp = queue.shift();

    // If left child is empty, insert the new node here
    if (temp.left === null) {
        temp.left = new Node(key);
        break;
    } else {
        queue.push(temp.left);
    }

    // If right child is empty, insert the new node here
    if (temp.right === null) {
        temp.right = new Node(key);
        break;
    } else {
        queue.push(temp.right);
    }
}

return root;

}

// In-order traversal function inorder(root) { if (root === null) return; inorder(root.left); process.stdout.write(root.data + " "); inorder(root.right); }

let root = new Node(2); root.left = new Node(3); root.right = new Node(4); root.left.left = new Node(5);

console.log("Inorder traversal before insertion: "); inorder(root); console.log();

let key = 6; root = insert(root, key);

console.log("Inorder traversal after insertion: "); inorder(root); console.log();

Output

Inorder traversal before insertion: 5 3 2 4 Inorder traversal after insertion: 5 3 6 2 4

3. Searching in Binary Tree

**Searching for a value in a binary tree means looking through the tree to find a node that has that value. Since binary trees do not have a specific order like binary search trees, we typically use any traversal method to search. The most common methods are **depth-first search (DFS) and **breadth-first search (BFS). In **DFS, we start from the **root and explore the depth nodes first. In BFS, we explore all the nodes at the present depth level before moving on to the nodes at the next level. We continue this process until we either find the node with the desired value or reach the end of the tree. If the tree is empty or the value isn't found after exploring all possibilities, we conclude that the value does not exist in the tree.

Here is the implementation of searching in a binary tree using Depth-First Search (DFS)

C++ `

#include using namespace std;

struct Node{ int data; Node *left, *right; Node(int d){ data = d; left = right = nullptr; } };

// Function to search for a value in the binary tree using DFS bool searchDFS(Node *root, int value){ // Base case: If the tree is empty or we've reached a leaf node if (root == nullptr) return false;

// If the node's data is equal to the value we are searching for
if (root->data == value) return true;

// Recursively search in the left and right subtrees
bool left_res = searchDFS(root->left, value);
bool right_res = searchDFS(root->right, value);

return left_res || right_res;

}

int main() { Node *root = new Node(2); root->left = new Node(3); root->right = new Node(4); root->left->left = new Node(5); root->left->right = new Node(6);

int value = 6;
if (searchDFS(root, value))
    cout << value << " is found in the binary tree" << endl;
else
    cout << value << " is not found in the binary tree" << endl;

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

struct Node { int data; struct Node* left; struct Node* right; };

// Function to search for a value in the binary tree using DFS int searchDFS(struct Node* root, int value) { // Base case: If the tree is empty or we've reached a leaf node if (root == NULL) return 0;

// If the node's data is equal to the value we are searching for
if (root->data == value) return 1;

// Recursively search in the left and right subtrees
int left_res = searchDFS(root->left, value);
int right_res = searchDFS(root->right, value);
  return left_res || right_res;

}

struct Node* createNode(int d) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = d; node->left = node->right = NULL; return node; }

int main() { struct Node* root = createNode(2); root->left = createNode(3); root->right = createNode(4); root->left->left = createNode(5); root->left->right = createNode(6);

int value = 6;
if (searchDFS(root, value))
    printf("%d is found in the binary tree\n", value);
else
    printf("%d is not found in the binary tree\n", value);

return 0;

}

Java

class Node { int data; Node left, right;

Node(int d){
    data = d;
    left = right = null;
}

}

public class GFG {

// Function to search for a value in the binary tree
// using DFS
static boolean searchDFS(Node root, int value){
    // Base case: If the tree is empty or we've reached
    // a leaf node
    if (root == null) return false;

    // If the node's data is equal to the value we are
    // searching for
    if (root.data == value) return true;
    
    // Recursively search in the left and right subtrees
    boolean left_res = searchDFS(root.left, value);
    boolean right_res = searchDFS(root.right, value);

    return left_res || right_res;
}

public static void main(String[] args){
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);
    root.left.right = new Node(6);

    int value = 6;
    if (searchDFS(root, value))
        System.out.println(
            value + " is found in the binary tree");
    else
        System.out.println(
            value + " is not found in the binary tree");
}

}

Python

class Node: def init(self, d): self.data = d self.left = None self.right = None

Function to search for a value in the binary tree using DFS

def searchDFS(root, value): # Base case: If the tree is empty or we've reached a leaf node if root is None: return False # If the node's data is equal to the value we are searching for if root.data == value: return True # Recursively search in the left and right subtrees left_res = searchDFS(root.left, value) right_res = searchDFS(root.right, value)

return left_res or right_res

if name == "main": root = Node(2) root.left = Node(3) root.right = Node(4) root.left.left = Node(5) root.left.right = Node(6)

value = 6
if searchDFS(root, value):
    print(f"{value} is found in the binary tree")
else:
    print(f"{value} is not found in the binary tree")

C#

using System;

class Node { public int data; public Node left, right;

public Node(int d){
    data = d;
    left = right = null;
}

}

class GFG {

// Function to search for a value in the binary tree
// using DFS
static bool SearchDFS(Node root, int value){
    // Base case: If the tree is empty or we've reached
    // a leaf node
    if (root == null) return false;
    
    // If the node's data is equal to the value we are
    // searching for
    if (root.data == value) return true;
    
    // Recursively search in the left and right subtrees
    bool left_res = SearchDFS(root.left, value);
    bool right_res = SearchDFS(root.right, value);

    return left_res || right_res;
}

static void Main(string[] args){
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);
    root.left.right = new Node(6);

    int value = 6;
    if (SearchDFS(root, value))
        Console.WriteLine(String.Format(
            "{0} is found in the binary tree", value));
    else
        Console.WriteLine(String.Format(
            "{0} is not found in the binary tree",
            value));
}

}

` JavaScript ``

class Node { constructor(d) { this.data = d; this.left = null; this.right = null; } }

// Function to search for a value in the binary tree using DFS function searchDFS(root, value) { // Base case: If the tree is empty or we've reached a leaf node if (root === null) { return false; } // If the node's data is equal to the value we are searching for if (root.data === value) { return true; } // Recursively search in the left and right subtrees const left_res = searchDFS(root.left, value); const right_res = searchDFS(root.right, value);

return left_res || right_res;

}

// Creating the binary tree const root = new Node(2); root.left = new Node(3); root.right = new Node(4); root.left.left = new Node(5); root.left.right = new Node(6);

const value = 6; if (searchDFS(root, value)) { console.log(${value} is found in the binary tree); } else { console.log(${value} is not found in the binary tree); }

Output

6 is found in the binary tree

4. Deletion in Binary Tree

Deleting a node from a binary tree means removing a specific node while keeping the tree's structure. First, we need to find the node that want to delete by traversing through the tree using any traversal method. Then replace the node's value with the value of the last node in the tree (found by traversing to the rightmost leaf), and then delete that last node. This way, the tree structure won't be effected. And remember to check for special cases, like trying to delete from an empty tree, to avoid any issues.

**Note: There is no specific rule of deletion but we always make sure that during deletion the binary tree proper should be preserved.

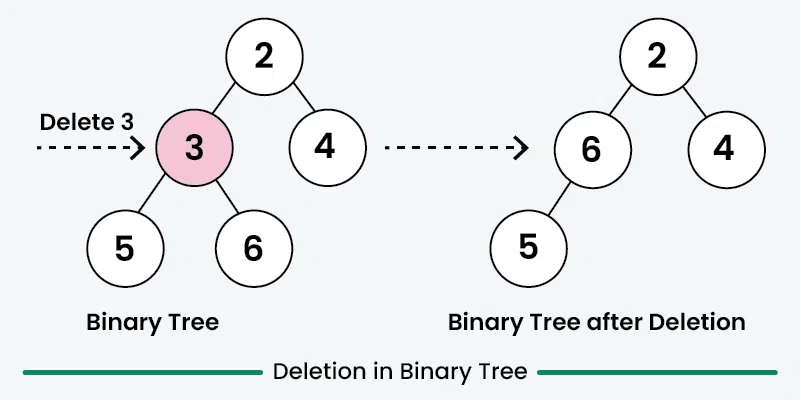
Deletion-in-Binary-Tree

Deletion in Binary Tree

C++ `

#include <bits/stdc++.h> using namespace std;

struct Node { int data; Node* left, * right; Node(int d) { data = d; left = right = nullptr; } };

// Function to delete a node from the binary tree Node* deleteNode(Node* root, int val) { if (root == nullptr) return nullptr; // Use a queue to perform BFS queue<Node*> q; q.push(root); Node* target = nullptr;

// Find the target node
while (!q.empty()) {
    Node* curr = q.front();
    q.pop();

    // Check for current node is the target node to delete
    if (curr->data == val) {
        target = curr;
        break;
    }
    // Add children to the queue
    if (curr->left) q.push(curr->left);
    if (curr->right) q.push(curr->right);
}
// If target node is not found, return the original tree
if (target == nullptr) return root;

// Find the deepest rightmost node and its parent
pair<Node*, Node*> last = {nullptr, nullptr};
queue<pair<Node*, Node*>> q1;
q1.push({root, nullptr});

while (!q1.empty()) {
    auto curr = q1.front();
    q1.pop();

    // Update the last
    last = curr;
  
    if (curr.first->left) 
      q1.push({curr.first->left, curr.first});
    if (curr.first->right) 
      q1.push({curr.first->right, curr.first});
}

Node* lastNode = last.first;
Node* lastParent = last.second;

// Replace target's value with the last node's value
target->data = lastNode->data;

// Remove the last node
if (lastParent) {
    if (lastParent->left==lastNode)lastParent->left = nullptr;
    else lastParent->right = nullptr;
    delete lastNode;
} else {
    // If the last node was the root
    delete lastNode;
    return nullptr;
}
return root;

}

void inOrder(Node* root) { if (root == nullptr) return; inOrder(root->left); cout << root->data << " "; inOrder(root->right); }

int main() { // Creating a simple binary tree Node *root = new Node(2); root->left = new Node(3); root->right = new Node(4); root->left->left = new Node(5); root->left->right = new Node(6);

cout << "Original tree (in-order): ";
inOrder(root);

int valToDel = 3;
root = deleteNode(root, valToDel);

cout <<"\nTree after deleting " << valToDel << " (in-order): ";
inOrder(root);
cout << endl;

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

struct Node { int data; struct Node* left; struct Node* right; };

struct Node* createNode(int d);

// Function to delete a node from the binary tree struct Node* deleteNode(struct Node* root, int val) { if (root == NULL) return NULL;

// Use a queue to perform BFS
struct Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
struct Node* target = NULL;

// Find the target node
while (front < rear) {
    struct Node* curr = queue[front++];

    if (curr->data == val) {
        target = curr;
        break;
    }
    if (curr->left) queue[rear++] = curr->left;
    if (curr->right) queue[rear++] = curr->right;
}
if (target == NULL) return root;

// Find the deepest rightmost node and its parent
struct Node* lastNode = NULL;
struct Node* lastParent = NULL;
struct Node* queue1[100];
int front1 = 0, rear1 = 0;
queue1[rear1++] = root;
struct Node* parents[100];
parents[rear1 - 1] = NULL;

while (front1 < rear1) {
    struct Node* curr = queue1[front1];
    struct Node* parent = parents[front1++];

    lastNode = curr;
    lastParent = parent;

    if (curr->left) {
        queue1[rear1] = curr->left;
        parents[rear1++] = curr;
    }
    if (curr->right) {
        queue1[rear1] = curr->right;
        parents[rear1++] = curr;
    }
}

// Replace target's value with the last node's value
target->data = lastNode->data;

// Remove the last node
if (lastParent) {
    if (lastParent->left == lastNode) lastParent->left = NULL;
    else lastParent->right = NULL;
    free(lastNode);
} else {
    free(lastNode);
    return NULL;
}

return root;

}

void inorder(struct Node* root) { if (root == NULL) return; inorder(root->left); printf("%d ", root->data); inorder(root->right); }

// Function to create a new node struct Node* createNode(int d) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = d; newNode->left = NULL; newNode->right = NULL; return newNode; }

int main() { struct Node* root = createNode(2); root->left = createNode(3); root->right = createNode(4); root->left->left = createNode(5); root->left->right = createNode(6);

printf("Original tree (in-order): ");
inorder(root);
printf("\n");

int valToDel = 3;
root = deleteNode(root, valToDel);

printf("Tree after deleting %d (in-order): ", valToDel);
inorder(root);
printf("\n");

return 0;

}

Java

import java.util.LinkedList; import java.util.Queue;

class Node { int data; Node left, right;

Node(int d) {
    data = d;
    left = right = null;
}

}

class GfG { // Function to delete a node from the binary tree static Node deleteNode(Node root, int val) { if (root == null) return null;

    // Use a queue to perform BFS
    Queue<Node> q = new LinkedList<>();
    q.add(root);
    Node target = null;

    // Find the target node
    while (!q.isEmpty()) {
        Node curr = q.poll();

        if (curr.data == val) {
            target = curr;
            break;
        }
        if (curr.left != null) q.add(curr.left);
        if (curr.right != null) q.add(curr.right);
    }
    if (target == null) return root;

    // Find the deepest rightmost node and its parent
    Node lastNode = null;
    Node lastParent = null;
    Queue<Node> q1 = new LinkedList<>();
    Queue<Node> parentQueue = new LinkedList<>();
    q1.add(root);
    parentQueue.add(null);

    while (!q1.isEmpty()) {
        Node curr = q1.poll();
        Node parent = parentQueue.poll();

        lastNode = curr;
        lastParent = parent;

        if (curr.left != null) {
            q1.add(curr.left);
            parentQueue.add(curr);
        }
        if (curr.right != null) {
            q1.add(curr.right);
            parentQueue.add(curr);
        }
    }

    // Replace target's value with the last node's value
    target.data = lastNode.data;

    // Remove the last node
    if (lastParent != null) {
        if (lastParent.left == lastNode) lastParent.left = null;
        else lastParent.right = null;
    } else {
        return null;
    }
    return root;
}

// In-order traversal
static void inorder(Node root) {
    if (root == null) return;
    inorder(root.left);
    System.out.print(root.data + " ");
    inorder(root.right);
}

public static void main(String[] args) {
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);
    root.left.right = new Node(6);

    System.out.print("Original tree (in-order): ");
    inorder(root);
    System.out.println();

    int valToDel = 3;
    root = deleteNode(root, valToDel);

    System.out.print("Tree after deleting " + valToDel + " (in-order): ");
    inorder(root);
    System.out.println();
}

}

Python

from collections import deque

class Node: def init(self, d): self.data = d self.left = None self.right = None

Function to delete a node from the binary tree

def deleteNode(root, val): if root is None: return None

# Use a queue to perform BFS
queue = deque([root])
target = None

# Find the target node
while queue:
    curr = queue.popleft()

    if curr.data == val:
        target = curr
        break
    if curr.left:
        queue.append(curr.left)
    if curr.right:
        queue.append(curr.right)

if target is None:
    return root

# Find the deepest rightmost node and its parent
last_node = None
last_parent = None
queue = deque([(root, None)])

while queue:
    curr, parent = queue.popleft()
    last_node = curr
    last_parent = parent

    if curr.left:
        queue.append((curr.left, curr))
    if curr.right:
        queue.append((curr.right, curr))

# Replace target's value with the last node's value
target.data = last_node.data

# Remove the last node
if last_parent:
    if last_parent.left == last_node:
        last_parent.left = None
    else:
        last_parent.right = None
else:
    return None
return root

In-order traversal

def inorder(root): if root is None: return inorder(root.left) print(root.data, end=" ") inorder(root.right)

if name == "main": root = Node(2) root.left = Node(3) root.right = Node(4) root.left.left = Node(5) root.left.right = Node(6)

print("Original tree (in-order): ", end="")
inorder(root)
print()

val_to_del = 3
root = deleteNode(root, val_to_del)

print(f"Tree after deleting {val_to_del} (in-order): ", end="")
inorder(root)
print()

C#

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int d) {
    data = d;
    left = right = null;
}

}

class GfG { // Function to delete a node from the binary tree static Node DeleteNode(Node root, int val) { if (root == null) return null;

    // Use a queue to perform BFS
    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);
    Node target = null;

    // Find the target node
    while (q.Count > 0) {
        Node curr = q.Dequeue();

        if (curr.data == val) {
            target = curr;
            break;
        }
        if (curr.left != null) q.Enqueue(curr.left);
        if (curr.right != null) q.Enqueue(curr.right);
    }
    if (target == null) return root;

    // Find the deepest rightmost node and its parent
    Node lastNode = null;
    Node lastParent = null;
    Queue<(Node, Node)> q1 = new Queue<(Node, Node)>();
    q1.Enqueue((root, null));

    while (q1.Count > 0) {
        var (curr, parent) = q1.Dequeue();
        lastNode = curr;
        lastParent = parent;

        if (curr.left != null) q1.Enqueue((curr.left, curr));
        if (curr.right != null) q1.Enqueue((curr.right, curr));
    }

    // Replace target's value with the last node's value
    target.data = lastNode.data;

    // Remove the last node
    if (lastParent != null) {
        if (lastParent.left == lastNode) lastParent.left = null;
        else lastParent.right = null;
    } else {
        return null;
    }
    return root;
}

// In-order traversal
static void Inorder(Node root) {
    if (root == null) return;
    Inorder(root.left);
    Console.Write(root.data + " ");
    Inorder(root.right);
}

static void Main() {
    Node root = new Node(2);
    root.left = new Node(3);
    root.right = new Node(4);
    root.left.left = new Node(5);
    root.left.right = new Node(6);

    Console.Write("Original tree (in-order): ");
    Inorder(root);
    Console.WriteLine();

    int valToDel = 3;
    root = DeleteNode(root, valToDel);

    Console.Write("Tree after deleting " 
                  + valToDel + " (in-order): ");
    Inorder(root);
    Console.WriteLine();
}

}

` JavaScript ``

class Node { constructor(d) { this.data = d; this.left = null; this.right = null; } }

// Function to delete a node from the binary tree function deleteNode(root, val) { if (root === null) return null;

// Use a queue to perform BFS
let queue = [root];
let target = null;

// Find the target node
while (queue.length > 0) {
    let curr = queue.shift();

    if (curr.data === val) {
        target = curr;
        break;
    }
    if (curr.left) queue.push(curr.left);
    if (curr.right) queue.push(curr.right);
}
if (target === null) return root;

// Find the deepest rightmost node and its parent
let lastNode = null;
let lastParent = null;
queue = [{ node: root, parent: null }];

while (queue.length > 0) {
    let { node: curr, parent } = queue.shift();
    lastNode = curr;
    lastParent = parent;

    if (curr.left) queue.push({ node: curr.left, parent: curr });
    if (curr.right) queue.push({ node: curr.right, parent: curr });
}

// Replace target's value with the last node's value
target.data = lastNode.data;

// Remove the last node
if (lastParent) {
    if (lastParent.left === lastNode) lastParent.left = null;
    else lastParent.right = null;
} else {
    return null;
}
return root;

}

// In-order traversal function inorder(root) { if (root === null) return; inorder(root.left); console.log(root.data + " "); inorder(root.right); }

let root = new Node(2); root.left = new Node(3); root.right = new Node(4); root.left.left = new Node(5); root.left.right = new Node(6);

console.log("Original tree (in-order): "); inorder(root); console.log();

let valToDel = 3; root = deleteNode(root, valToDel);

console.log(Tree after deleting ${valToDel} (in-order): ); inorder(root); console.log();

Output

Original tree (in-order): 5 3 6 2 4 Tree after deleting 3 (in-order): 5 6 2 4

**Auxiliary Operations On Binary Tree

Complexity Analysis of Binary Tree Operations

Here’s the complexity analysis for specific binary tree operations:

**Operation	**Time Complexity	**Auxiliary Space
**In-Order Traversal	O(n)	O(n)
**Pre-Order Traversal	O(n)	O(n)
**Post-Order Traversal	O(n)	O(n)
**Insertion (Unbalanced)	O(n)	O(n)
**Searching (Unbalanced)	O(n)	O(n)
**Deletion (Unbalanced)	O(n)	O(n)

**Note: We can use **Morris Traversalto traverse all the nodes of the binary tree in O(n) time complexity but with O(1) auxiliary space.

Advantages of Binary Tree

**Efficient Search: Binary Search Trees (a variation of Binary Tree) are efficient when searching for a specific element, as each node has at most two child nodes when compared to linked list and arrays
**Memory Efficient: Binary trees require lesser memory as compared to other tree data structures, therefore memory-efficient.
Binary trees are relatively easy to implement and understand as each node has at most two children, left child and right child.

Disadvantages of Binary Tree

**Limited structure: Binary trees are limited to two child nodes per node, which can limit their usefulness in certain applications. For example, if a tree requires more than two child nodes per node, a different tree structure may be more suitable.
**Unbalanced trees: Unbalanced binary trees, where one subtree is significantly larger than the other, can lead to inefficient search operations. This can occur if the tree is not properly balanced or if data is inserted in a non-random order.
**Space inefficiency: Binary trees can be space inefficient when compared to other data structures like arrays and linked list. This is because each node requires two child references or pointers, which can be a significant amount of memory overhead for large trees.
**Slow performance in worst-case scenarios: In the worst-case scenario, a binary tree can become degenerate or skewed, meaning that each node has only one child. In this case, search operations in Binary Search Tree (a variation of Binary Tree) can degrade to O(n) time complexity, where n is the number of nodes in the tree.

**Applications of Binary Tree

Binary Tree can be used to represent hierarchical data.
Huffman Coding trees are used in **data compression algorithms.
Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
Useful for indexing segmented at the database is useful in storing cache in the system,
Binary trees can be used to implement decision trees, a type of machine learning algorithm used for classification and regression analysis.

Conclusion:

Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.

Introduction to Binary Tree (original) (raw)

**Representation of Binary Tree

Create/Declare a Node of a Binary Tree

A Python class that represents

an individual node in a Binary Tree

Example for Creating a Binary Tree

Initialize and allocate memory for tree nodes

Connect binary tree nodes

Terminologies in Binary Tree

Properties of Binary Tree

Types of Binary Tree

**Operations On Binary Tree

1. Traversal in Binary Tree

In-order DFS: Left, Root, Right

Pre-order DFS: Root, Left, Right

Post-order DFS: Left, Right, Root

BFS: Level order traversal

2. Insertion in Binary Tree

Function to insert a new node in the binary tree

In-order traversal

3. Searching in Binary Tree

Function to search for a value in the binary tree using DFS

4. Deletion in Binary Tree

Function to delete a node from the binary tree

In-order traversal

**Auxiliary Operations On Binary Tree

Complexity Analysis of Binary Tree Operations

Advantages of Binary Tree

Disadvantages of Binary Tree

**Applications of Binary Tree

Conclusion:

Related Articles: