Introduction to Recursion (original) (raw)

The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function.

**Need of Recursion

**Steps to Implement Recursion

S**tep1 – Define a base case: Identify the simplest (or base) case for which the solution is known or trivial. This is the stopping condition for the recursion, as it prevents the function from infinitely calling itself.

**Step2 – Define a recursive case: Define the problem in terms of smaller subproblems. Break the problem down into smaller versions of itself, and call the function recursively to solve each subproblem.

**Step3 – Ensure the recursion terminates: Make sure that the recursive function eventually reaches the base case, and does not enter an infinite loop.

**Step4 – Combine the solutions: Combine the solutions of the subproblems to solve the original problem.

**Example 1 : Sum of Natural Numbers

Let us consider a problem to find the sum of natural numbers, there are several ways of doing that but the simplest approach is simply to add the numbers starting from 0 to n.

**Comparison of Recursive and Iterative Approaches

Approach Complexity Memory Usage
**Iterative Approach O(n) O(1)
**Recursive Approach O(n) O(n)

C++ `

#include using namespace std;

// Recursive function to find the sum of // numbers from 0 to n int findSum(int n) { // Base case if (n == 1) return 1; 

// Recursive case 
return n + findSum(n - 1);

}

int main() { int n = 5; cout << findSum(n); return 0; }

C

#include <stdio.h>

// Recursive function to find the sum of // numbers from 0 to n int findSum(int n) { // Base case if (n == 1) return 1; 

// Recursive case 
return n + findSum(n - 1);

}

int main() { int n = 5; printf("%d", findSum(n)); return 0; }

Java

public class Main { // Recursive function to find the sum of // numbers from 0 to n static int findSum(int n) { // Base case if (n == 1) return 1; 

    // Recursive case 
    return n + findSum(n - 1);
}

public static void main(String[] args) {
    int n = 5;
    System.out.println(findSum(n));
}

}

Python

def findSum(n): # Base case if n == 1: return 1

# Recursive case 
return n + findSum(n - 1)

n = 5 print(findSum(n))

C#

using System;

class Program { // Recursive function to find the sum of // numbers from 0 to n static int FindSum(int n) { // Base case if (n == 1) return 1;

    // Recursive case 
    return n + FindSum(n - 1);
}

static void Main() {
    int n = 5;
    Console.WriteLine(FindSum(n));
}

}

JavaScript

// Recursive function to find the sum of // numbers from 0 to n function findSum(n) { // Base case if (n === 1) return 1;

// Recursive case 
return n + findSum(n - 1);

}

let n = 5; console.log(findSum(n));

`

**What is the base condition in recursion?
A recursive program stops at a base condition. There can be more than one base conditions in a recursion. In the above program, the base condition is when n = 1.

**How a particular problem is solved using recursion?
The idea is to represent a problem in terms of one or more smaller problems, and add one or more base conditions that stop the recursion.

**Example 2 : Factorial of a Number

The factorial of a number n (where n >= 0) is the product of all positive integers from 1 to n. To compute the factorial recursively, we calculate the factorial of n by using the factorial of (n-1). The base case for the recursive function is when n = 0, in which case we return 1.

C++ `

#include using namespace std;

int fact(int n) { // BASE CONDITION if (n == 0) return 1;

return n * fact(n - 1);

}

int main() { cout << "Factorial of 5 : " << fact(5); return 0; }

C

#include <stdio.h>

int fact(int n) {

// BASE CONDITION
if (n == 0)
    return 1;

return n * fact(n - 1);

}

int main() { printf("Factorial of 5 : %d\n", fact(5)); return 0; }

Java

public class GfG { public static int fact(int n) {

    // BASE CONDITION
    if (n == 0)
        return 1;
  
    return n * fact(n - 1);
}

public static void main(String[] args) {
    System.out.println("Factorial of 5 : " + fact(5));
}

}

Python

def fact(n):

# BASE CONDITION
if n == 0:
    return 1
return n * fact(n - 1)

print("Factorial of 5 : ", fact(5))

C#

using System;

class Program { static int Fact(int n) {

    // BASE CONDITION
    if (n == 0)
        return 1;
    
    return n * Fact(n - 1);
}

static void Main() {
    Console.WriteLine("Factorial of 5 : " + Fact(5));
}

}

JavaScript

function fact(n) {

// BASE CONDITION
if (n === 0)
    return 1;

return n * fact(n - 1);

}

console.log("Factorial of 5 : " + fact(5));

PHP

n∗fact(n * fact(n∗fact(n - 1); } echo "Factorial of 5 : " . fact(5); ?>

`

Output

Factorial of 5 : 120

**Illustration of the above code:

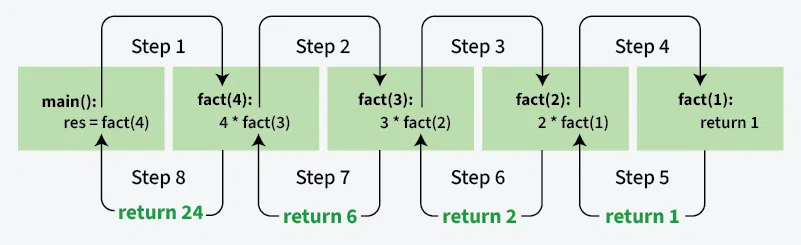
factorial

**When does Stack Overflow error occur in recursion?

If the base case is not reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.

int fact(int n)
{
// wrong base case (it may cause stack overflow).
if (n == 100)
return 1;
else
return n*fact(n-1);
}

**What is the difference between direct and indirect recursion?

A function is called **direct recursive if it calls itself directly during its execution. In other words, the function makes a recursive call to itself within its own body.

An **indirect recursive function is one that calls another function, and that other function, in turn, calls the original function either directly or through other functions. This creates a chain of recursive calls involving multiple functions, as opposed to direct recursion, where a function calls itself.

****// An example of direct recursion**
void directRecFun()
{
// Some code….

directRecFun();

// Some code…
}

****// An example of indirect recursion**
void indirectRecFun1()
{
// Some code…

indirectRecFun2();

// Some code…
}
void indirectRecFun2()
{
// Some code…

indirectRecFun1();

// Some code…
}

**What is the difference between tail and non-tail recursion?

A recursive function is tail recursive when a recursive call is the last thing executed by the function.

Please refer tail recursion for details.

**How memory is allocated to different function calls in recursion?

Recursion uses more memory to store data of every recursive call in an internal function call stack.

When any function is called from main(), the memory is allocated to it on the stack. A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to the calling function and a different copy of local variables is created for each function call. When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.
Let us take the example of how recursion works by taking a simple function.

C++ `

// A C++ program to demonstrate working of // recursion #include <bits/stdc++.h> using namespace std;

void printFun(int test) { if (test < 1) return; else { cout << test << " "; printFun(test - 1); // statement 2 cout << test << " "; return; } }

// Driver Code int main() { int test = 3; printFun(test); }

C

// A C program to demonstrate working of recursion #include <stdio.h>

void printFun(int test) { if (test < 1) return; else { printf("%d ", test); printFun(test - 1); // statement 2 printf("%d ", test); return; } }

// Driver Code int main() { int test = 3; printFun(test); return 0; }

Java

// A Java program to demonstrate working of // recursion class GFG { static void printFun(int test) { if (test < 1) return; else { System.out.printf("%d ", test); printFun(test - 1); // statement 2 System.out.printf("%d ", test); return; } }

// Driver Code
public static void main(String[] args)
{
    int test = 3;
    printFun(test);
}

}

// This code is contributed by // Smitha Dinesh Semwal

Python

A Python 3 program to

demonstrate working of

recursion

def printFun(test):

if (test < 1):
    return
else:

    print(test, end=" ")
    printFun(test-1)  # statement 2
    print(test, end=" ")
    return

Driver Code

test = 3 printFun(test)

This code is contributed by

Smitha Dinesh Semwal

C#

// A C# program to demonstrate // working of recursion using System;

class GFG {

// function to demonstrate
// working of recursion
static void printFun(int test)
{
    if (test < 1)
        return;
    else {
        Console.Write(test + " ");

        // statement 2
        printFun(test - 1);

        Console.Write(test + " ");
        return;
    }
}

// Driver Code
public static void Main(String[] args)
{
    int test = 3;
    printFun(test);
}

}

// This code is contributed by Anshul Aggarwal.

JavaScript

// A JavaScript program to demonstrate working of recursion function printFun(test) { if (test < 1) return; else { console.log(test); printFun(test - 1); // statement 2 console.log(test); return; } }

// Driver Code let test = 3; printFun(test);

PHP

`

**Initial Call: When printFun(3) is called from main(), memory is allocated for printFun(3). The local variable test is initialized to 3, and statements 1 to 4 are pushed onto the stack.

**First Recursive Call:

**Second Recursive Call:

**Third Recursive Call:

**Base Case: When printFun(0) is called, it hits the base case (if statement) and returns control to printFun(1).

**Returning from Recursion:

**Output: As a result, the output will print the values in the following order:

The memory stack grows with each function call and shrinks as the recursion unwinds, following the LIFO structure.

**Recursion VS Iteration

**SR No. **Recursion **Iteration
1) Terminates when the base case becomes true. Terminates when the loop condition becomes false.
2) Logic is built in terms of smaller problems. Logic is built using iterating over something.
3) Every recursive call needs extra space in the stack memory. Every iteration does not require any extra space.
4) Smaller code size. Larger code size.

**What are the advantages of recursive programming over iterative programming?

**What are the disadvantages of recursive programming over iterative programming?

Note every recursive program can be written iteratively and vice versa is also true.

**Example 3 : Fibonacci with Recursion

Write a program and recurrence relation to find the Fibonacci series of n where n >= 0.

**Mathematical Equation:

n if n == 0, n == 1;
fib(n) = fib(n-1) + fib(n-2) otherwise;

**Recurrence Relation:

T(n) = T(n-1) + T(n-2) + O(1)

C++ `

// C++ code to implement Fibonacci series #include <bits/stdc++.h> using namespace std;

// Function for fibonacci

int fib(int n) { // Stop condition if (n == 0) return 0;

// Stop condition
if (n == 1 || n == 2)
    return 1;

// Recursion function
else
    return (fib(n - 1) + fib(n - 2));

}

// Driver Code int main() { // Initialize variable n. int n = 5; cout<<"Fibonacci series of 5 numbers is: ";

// for loop to print the fibonacci series.
for (int i = 0; i < n; i++) 
{
    cout<<fib(i)<<" ";
}
return 0;

}

C

// C code to implement Fibonacci series #include <stdio.h>

// Function for fibonacci int fib(int n) { // Stop condition if (n == 0) return 0;

// Stop condition
if (n == 1 || n == 2)
    return 1;

// Recursion function
else
    return (fib(n - 1) + fib(n - 2));

}

// Driver Code int main() { // Initialize variable n. int n = 5; printf("Fibonacci series " "of %d numbers is: ", n);

// for loop to print the fibonacci series.
for (int i = 0; i < n; i++) {
    printf("%d ", fib(i));
}
return 0;

}

Java

// Java code to implement Fibonacci series import java.util.*;

class GFG {

// Function for fibonacci static int fib(int n) { // Stop condition if (n == 0) return 0;

// Stop condition
if (n == 1 || n == 2)
    return 1;

// Recursion function
else
    return (fib(n - 1) + fib(n - 2));

}

// Driver Code public static void main(String []args) {

// Initialize variable n.
int n = 5;
System.out.print("Fibonacci series of 5 numbers is: ");

// for loop to print the fibonacci series.
for (int i = 0; i < n; i++) 
{
    System.out.print(fib(i)+" ");
}

} }

// This code is contributed by rutvik_56.

Python

Python code to implement Fibonacci series

Function for fibonacci

def fib(n):

# Stop condition
if (n == 0):
    return 0

# Stop condition
if (n == 1 or n == 2):
    return 1

# Recursion function
else:
    return (fib(n - 1) + fib(n - 2))

Driver Code

Initialize variable n.

n = 5; print("Fibonacci series of 5 numbers is :",end=" ")

for loop to print the fibonacci series.

for i in range(0,n): print(fib(i),end=" ")

C#

using System;

public class GFG {

// Function for fibonacci static int fib(int n) {

// Stop condition
if (n == 0)
  return 0;

// Stop condition
if (n == 1 || n == 2)
  return 1;

// Recursion function
else
  return (fib(n - 1) + fib(n - 2));

}

// Driver Code static public void Main () {

// Initialize variable n.
int n = 5;
Console.Write("Fibonacci series of 5 numbers is: ");

// for loop to print the fibonacci series.
for (int i = 0; i < n; i++) 
{
  Console.Write(fib(i) + " ");
}

} }

// This code is contributed by avanitrachhadiya2155

JavaScript

// Function for fibonacci function fib(n) { // Stop condition if (n === 0) return 0;

// Stop condition
if (n === 1 || n === 2) return 1;

// Recursion function
return fib(n - 1) + fib(n - 2);

}

// Driver Code let n = 5; console.log("Fibonacci series of 5 numbers is:");

// for loop to print the fibonacci series. for (let i = 0; i < n; i++) { console.log(fib(i) + " "); }

`

Output

Fibonacci series of 5 numbers is: 0 1 1 2 3

**Recursion Tree for the above Code:

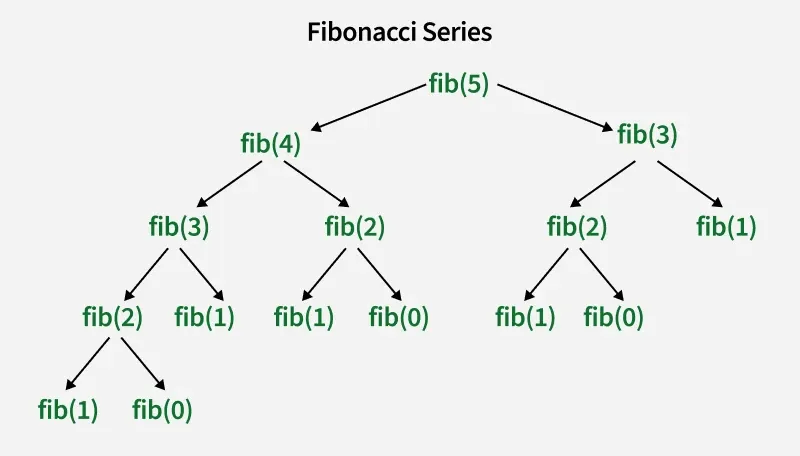
Fibonacci-series

fibonacci series

Common Applications of Recursion

  1. **Tree and Graph Traversal: Used for systematically exploring nodes/vertices in data structures like trees and graphs.
  2. **Sorting Algorithms: Algorithms like quicksort and merge sort divide data into subarrays, sort them recursively, and merge them.
  3. **Divide-and-Conquer Algorithms: Algorithms like binary search break problems into smaller subproblems using recursion.
  4. **Fractal Generation: Recursion helps generate fractal patterns, such as the Mandelbrot set, by repeatedly applying a recursive formula.
  5. **Backtracking Algorithms: Used for problems requiring a sequence of decisions, where recursion explores all possible paths and backtracks when needed.
  6. **Memoization: Involves caching results of recursive function calls to avoid recomputing expensive subproblems.

These are just a few examples of the many applications of recursion in computer science and programming. Recursion is a versatile and powerful tool that can be used to solve many different types of problems.

**Summary of Recursion:

**Output based practice problems for beginners:
Practice Questions for Recursion | Set 1
Practice Questions for Recursion | Set 2
Practice Questions for Recursion | Set 3
Practice Questions for Recursion | Set 4
Practice Questions for Recursion | Set 5
Practice Questions for Recursion | Set 6
Practice Questions for Recursion | Set 7
Quiz on Recursion
Coding Practice on Recursion:
All Articles on Recursion
Recursive Practice Problems with Solutions