Introduction to Sorting Techniques – Data Structure and Algorithm Tutorials (original) (raw)
Last Updated : 21 Oct, 2024
**Sorting refers to rearrangement of a given array or list of elements according to a comparison operator on the elements. The comparison operator is used to decide the new order of elements in the respective data structure.

Why Sorting Algorithms are Important
The sorting algorithm is important in Computer Science because it reduces the complexity of a problem. There is a wide range of applications for these algorithms, including searching algorithms, database algorithms, divide and conquer methods, and data structure algorithms.
In the following sections, we list some important scientific applications where sorting algorithms are used
- When you have hundreds of datasets you want to print, you might want to arrange them in some way.
- Once we get the data sorted, we can get the k-th smallest and k-th largest item in O(1) time.
- Searching any element in a huge data set becomes easy. We can use Binary search method for search if we have sorted data. So, Sorting become important here.
- They can be used in software and in conceptual problems to solve more advanced problems.
Sorting Basics
- **In-place Sorting****:** An in-place sorting algorithm uses **constant space for producing the output (modifies the given array only. Examples: Selection Sort, Bubble Sort, Insertion Sort and Heap Sort.
- **Internal Sorting: Internal Sorting is when all the data is placed in the **main memory or **internal memory. In internal sorting, the problem cannot take input beyond allocated memory size.
- **External Sorting : External Sorting is when all the data that needs to be sorted need not to be placed in memory at a time, the sorting is called external sorting. External Sorting is used for the massive amount of data. For example Merge sort can be used in external sorting as the whole array does not have to be present all the time in memory,
- **Stable sorting****:** When two same items appear in the **same **order in sorted data as in the original array called stable sort. Examples: Merge Sort, Insertion Sort, Bubble Sort.
- **Hybrid Sorting****:** A sorting algorithm is called Hybrid if it uses more than one standard sorting algorithms to sort the array. The idea is to take advantages of multiple sorting algorithms. For example IntroSort uses Insertions sort and Quick Sort.
Types of Sorting Techniques
There are various sorting algorithms are used in data structures. The following two types of sorting algorithms can be broadly classified:
- **Comparison-based: We compare the elements in a comparison-based sorting algorithm)
- **Non-comparison-based: We do not compare the elements in a non-comparison-based sorting algorithm)
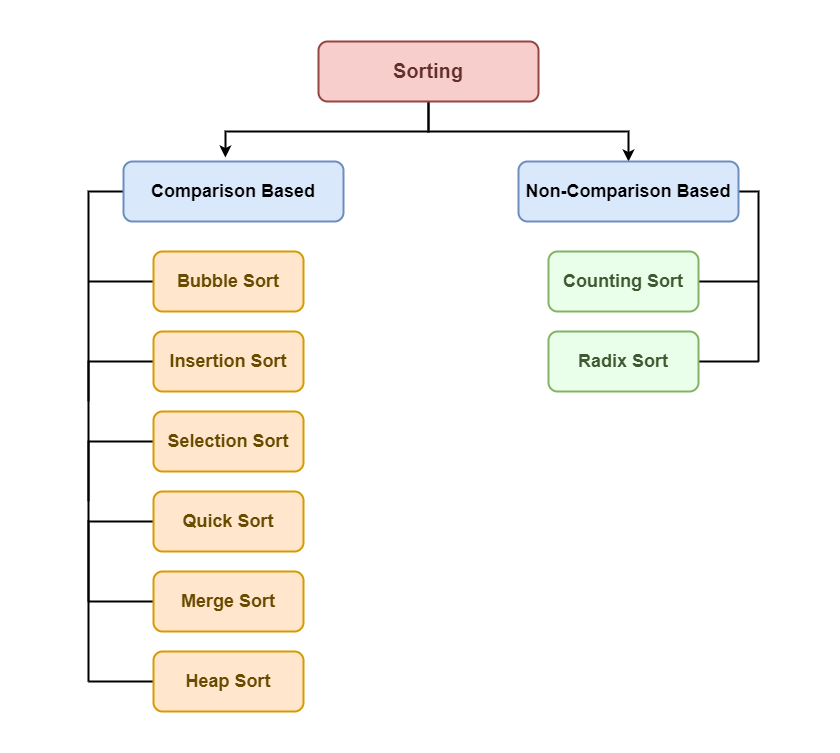
Sorting algorithm
Some of the most common sorting algorithms are:
Selection sort, Bubble sort, Insertion Sort, Cycle Sort, Merge Sort, 3-way Merge Sort, Quick sort, Heap sort and Counting sort
Some other Sorting algorithms:
Radix sort, Bucket sort, Shell sort, Tim Sort, Comb Sort, Pigeonhole sorting, Cocktail Sort, Strand sort, Bitonic Sort, Stooge Sort, Tag Sort, Tree sort, Cartesian Sort, Odd-Even Sort / Brick Sort, Gnome sort, Cocktail shaker sort
Comparison of Complexity Analysis of Sorting Algorithms:
| Name | Best Case | Average Case | Worst Case | Memory | Stable | Method Used |
|---|---|---|---|---|---|---|
| Quick Sort | n log n | n log n | n^{2} | log n | No | Partitioning |
| Merge Sort | n log n | n log n | n log n | n | Yes | Merging |
| Heap Sort | n log n | n log n | n log n | 1 | No | Selection |
| Insertion Sort | n | n^{2} | n^{2} | 1 | Yes | Insertion |
| Tim Sort | n | n log n | n log n | n | Yes | Insertion & Merging |
| Selection Sort | n^{2} | n^{2} | n^{2} | 1 | No | Selection |
| Shell Sort | n log n | n^{4/3} | n^{3/2} | 1 | No | Insertion |
| Bubble Sort | n | n^{2} | n^{2} | 1 | Yes | Exchanging |
| Tree Sort | n log n | n log n | n log n | n | Yes | Insertion |
| Cycle Sort | n^{2} | n^{2} | n^{2} | 1 | No | Selection |
| Strand Sort | n | n^{2} | n^{2} | n | Yes | Selection |
| Cocktail Shaker Sort | n | n^{2} | n^{2} | 1 | Yes | Exchanging |
| Comb Sort | n log n | n^{2} | n^{2} | 1 | No | Exchanging |
| Gnome Sort | n | n^{2} | n^{2} | 1 | Yes | Exchanging |
| Odd–even Sort | n | n^{2} | n^{2} | 1 | Yes | Exchanging Indexes: |